Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Famille de courbes qui dépendent d'un paramètre - Exercice 1
1 h 15 min
105
Soit un nombre réel non nul. On considère la fonction numérique réelle dont l'image fonctionnelle est donnée par l'expression :
.
On rappelle que décrit l'ensemble de tous les nombres réels strictement positifs.
.
On rappelle que décrit l'ensemble de tous les nombres réels strictement positifs.
Question 1
Etudier les variations de sur l'intervalle lorsque .
Correction
On considère que le nombre satisfait à la condition suivante :
Etude de la limite de lorsque
On a :
Posons ainsi , et on a . Dans ce cas, on a . On a alors :
Donc, on en déduit que :
.
Dans notre cas, la fonction est prolongeable par continuité en . Notons par le prolongement par continuité qui défini par :
Etude de la limite de lorsque
On a :
Posons ainsi , et on a . Dans ce cas, on a . On a alors :
Donc, on en déduit que :
.
Ainsi la courbe représentative de la fonction admet, en , la droite comme asymptote horizontale. De plus, la courbe représentative de la fonction attaque cette asymptote horizontale par le dessous. Sur le graphique final, elle est en couleur bleue.
Etude de la dérivabilité à l'origine
Comme on cherche la dérivabilité à l'origine, donc en , on va travailler avec le prolongement . On a doit alors étudier la limite suivante :
Posons ainsi , et on a . Dans ce cas, on a :
.
Donc la fonction est dérivable à l'origine (c'est-à-dire en ), et comme la tangente à l'origine est la droite d'équation réduite , dite "première bissectrice". Sur le graphique final, elle est en couleur verte.
Dérivée et variations sur
On a :
Or, si , alors (pour p réel) . Donc, on en déduit que , et . Ainsi, pour on obtient . Donc, sur l'intervalle , la fonction est strictement croissante. De plus comme , on en déduit que cette fonction est positive sur . Sur le graphique final, elle est en couleur rouge.
Par exemple, pour , ceci nous donne donc :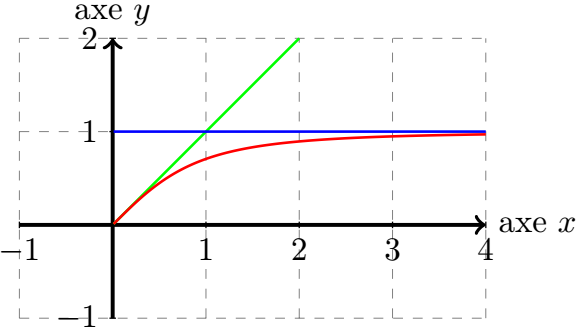
Etude de la limite de lorsque
On a :
Posons ainsi , et on a . Dans ce cas, on a . On a alors :
Donc, on en déduit que :
.
Dans notre cas, la fonction est prolongeable par continuité en . Notons par le prolongement par continuité qui défini par :
Etude de la limite de lorsque
On a :
Posons ainsi , et on a . Dans ce cas, on a . On a alors :
Donc, on en déduit que :
.
Ainsi la courbe représentative de la fonction admet, en , la droite comme asymptote horizontale. De plus, la courbe représentative de la fonction attaque cette asymptote horizontale par le dessous. Sur le graphique final, elle est en couleur bleue.
Etude de la dérivabilité à l'origine
Comme on cherche la dérivabilité à l'origine, donc en , on va travailler avec le prolongement . On a doit alors étudier la limite suivante :
Posons ainsi , et on a . Dans ce cas, on a :
.
Donc la fonction est dérivable à l'origine (c'est-à-dire en ), et comme la tangente à l'origine est la droite d'équation réduite , dite "première bissectrice". Sur le graphique final, elle est en couleur verte.
Dérivée et variations sur
On a :
Or, si , alors (pour p réel) . Donc, on en déduit que , et . Ainsi, pour on obtient . Donc, sur l'intervalle , la fonction est strictement croissante. De plus comme , on en déduit que cette fonction est positive sur . Sur le graphique final, elle est en couleur rouge.
Par exemple, pour , ceci nous donne donc :

Question 2
Etudier les variations de sur l'intervalle lorsque .
Correction
2) On considère que le nombre satisfait à la condition suivante :
Etude de la limite de lorsque
On a :
.
Si alors . Dans ce cas, on en déduit que :
.
Ainsi :
Dans notre cas, la fonction est prolongeable par continuité en . Notons par le prolongement par continuité qui défini par :
Etude de la limite de lorsque
On a :
Etude de la dérivabilité à l'origine
Comme on cherche la dérivabilité à l'origine, donc en , on va travailler avec le prolongement . On a doit alors étudier la limite suivante :
Comme , et donc également, on va faire usage de l'approximation affine suivante : . Ainsi, on a :
Comme alors cela implique que , et de fait où . Donc, on en déduit que :
Comme alors , et de fait on trouve que :
En conclusion, dans ce cas, la fonction n'est pas dérivable en . La tangente initiale, au point de coordonnées est verticale montante.
Dérivée et variations sur
On a :
Or, si , alors (pour p réel) . Donc, on en déduit que , et . Ainsi, pour on obtient . Donc, sur l'intervalle , la fonction est strictement croissante. De plus comme , on en déduit que cette fonction est strictement positive sur . Sur le graphique final, elle est en couleur rouge.
Par exemple, pour , ceci nous donne donc :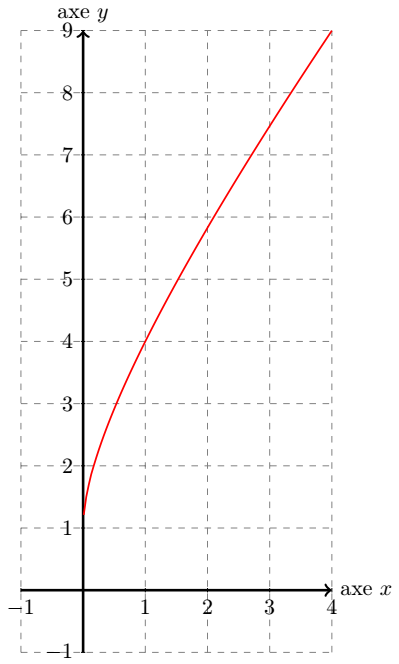
Etude de la limite de lorsque
On a :
.
Si alors . Dans ce cas, on en déduit que :
.
Ainsi :
Dans notre cas, la fonction est prolongeable par continuité en . Notons par le prolongement par continuité qui défini par :
Etude de la limite de lorsque
On a :
Etude de la dérivabilité à l'origine
Comme on cherche la dérivabilité à l'origine, donc en , on va travailler avec le prolongement . On a doit alors étudier la limite suivante :
Comme , et donc également, on va faire usage de l'approximation affine suivante : . Ainsi, on a :
Comme alors cela implique que , et de fait où . Donc, on en déduit que :
Comme alors , et de fait on trouve que :
En conclusion, dans ce cas, la fonction n'est pas dérivable en . La tangente initiale, au point de coordonnées est verticale montante.
Dérivée et variations sur
On a :
Or, si , alors (pour p réel) . Donc, on en déduit que , et . Ainsi, pour on obtient . Donc, sur l'intervalle , la fonction est strictement croissante. De plus comme , on en déduit que cette fonction est strictement positive sur . Sur le graphique final, elle est en couleur rouge.
Par exemple, pour , ceci nous donne donc :

Question 3
Etudier les variations de sur l'intervalle lorsque .
Correction
3) On considère que le nombre satisfait à la condition suivante :
Dans ce cas la fonction prend la forme suivante :
Il s'agit de l'équation réduite d'une droite, d'ordonnée à l'origine et de coefficient directeur . Ce dernier point implique que la droite est strictement croissante sur , donc à fortiori sur . Cette équation réduite de droite est donc dérivable, et donc continue, sur , donc à fortiori sur .
On a alors le graphique suivant :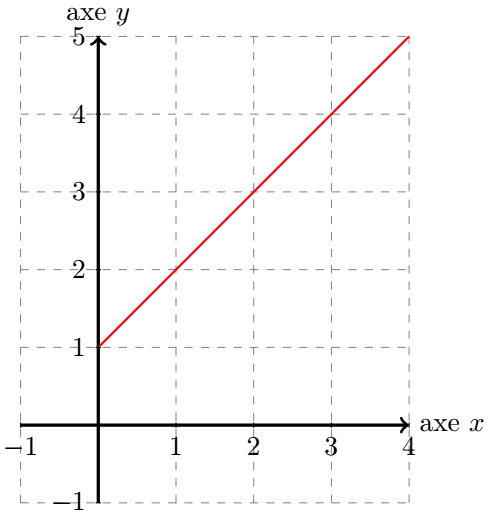
Dans ce cas la fonction prend la forme suivante :
Il s'agit de l'équation réduite d'une droite, d'ordonnée à l'origine et de coefficient directeur . Ce dernier point implique que la droite est strictement croissante sur , donc à fortiori sur . Cette équation réduite de droite est donc dérivable, et donc continue, sur , donc à fortiori sur .
On a alors le graphique suivant :

Question 4
Etudier les variations de sur l'intervalle lorsque .
Correction
4) On considère que le nombre satisfait à la condition suivante :
Etude de la limite de lorsque
On a :
.
Si alors . Dans ce cas, on en déduit que :
.
Ainsi :
Dans notre cas, la fonction est prolongeable par continuité en . Notons par le prolongement par continuité qui défini par :
Etude de la limite de lorsque
On a :
Etudions alors la possibilité éventuelle d'une asymptote oblique. Pour cela commençons par étudier la limite suivante :
Dans ce cas, dans la suite de la procédure de recherche asymptotique, étudions maintenant la limite suivante :
En factorisant par le terme , on trouve que :
Soit :
Ainsi, on en déduit que l'asymptote oblique à la coube, en , admet pour équation réduite . C'est la première bissectrice. De plus, la courbe représentative de attaque cette asymptote par le dessus. C'est la droite en bleue sur le graphique final.
Etude de la dérivabilité à l'origine
Comme on cherche la dérivabilité à l'origine, donc en , on va travailler avec le prolongement . On a doit alors étudier la limite suivante :
Comme , et donc également, on va faire usage de l'approximation affine suivante : . Ainsi, on a :
Comme alors cela implique que , et de fait . Donc, on en déduit que :
En conclusion, dans ce cas, la fonction est dérivable en . La tangente initiale, au point de coordonnées est horizontale. C'est la première bissectrice. C'est la droite en bleue sur le graphique final.
Graphiquement, on obtient avec :
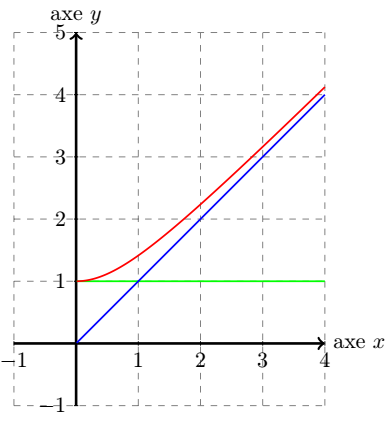
Etude de la limite de lorsque
On a :
.
Si alors . Dans ce cas, on en déduit que :
.
Ainsi :
Dans notre cas, la fonction est prolongeable par continuité en . Notons par le prolongement par continuité qui défini par :
Etude de la limite de lorsque
On a :
Etudions alors la possibilité éventuelle d'une asymptote oblique. Pour cela commençons par étudier la limite suivante :
Dans ce cas, dans la suite de la procédure de recherche asymptotique, étudions maintenant la limite suivante :
En factorisant par le terme , on trouve que :
Soit :
Ainsi, on en déduit que l'asymptote oblique à la coube, en , admet pour équation réduite . C'est la première bissectrice. De plus, la courbe représentative de attaque cette asymptote par le dessus. C'est la droite en bleue sur le graphique final.
Etude de la dérivabilité à l'origine
Comme on cherche la dérivabilité à l'origine, donc en , on va travailler avec le prolongement . On a doit alors étudier la limite suivante :
Comme , et donc également, on va faire usage de l'approximation affine suivante : . Ainsi, on a :
Comme alors cela implique que , et de fait . Donc, on en déduit que :
En conclusion, dans ce cas, la fonction est dérivable en . La tangente initiale, au point de coordonnées est horizontale. C'est la première bissectrice. C'est la droite en bleue sur le graphique final.
Graphiquement, on obtient avec :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.