Différentes équations - Exercice 3

Soit $$x$$ un nombre réel.
L'équation est définie pour $$\left\lbrace \begin{array}{rcl} x & \in & [-1 \,;\, 1] \\ \\ 2x & \in & [-1 \,;\, 1]\end{array} \right.$$ ce qui implique que $$x \in \left[ - \dfrac{1}{2} \,;\, \dfrac{1}{2} \right]$$.
De plus on a :
$$\left\lbrace \begin{array}{rcl} \arccos(x) & \in & [0 \,;\, \pi] \\ \\ \arcsin(2x) & \in & \left[ - \dfrac{\pi}{2} \,;\, \dfrac{\pi}{2} \right] \end{array} \right.$$
Pour que cela soit vérifier pour les deux termes $$\arccos(x)$$ et $$\arcsin(2x)$$ il faut que ces deux termes appartiennent à l'intervalle $$\left[ 0 \,;\, \dfrac{\pi}{2} \right]$$. Ceci revient à dire que :
$$\left\lbrace \begin{array}{rcl} x & \in & [0 \,;\, 1] \\ \\ 2x & \in & \left[ 0 \,;\, 1 \right] \end{array} \right.$$
Pour que cela soit effectivement possible, on va donc choisir $$x \in \left[0 \,;\, \dfrac{1}{2} \right]$$.
Donc l'équation $$E$$ va pouvoir s'écrire comme :
$$\forall x \in \left[0 \,;\, \dfrac{1}{2} \right], \,\, \sin \left( \arccos(x) \right) = \sin \left( \arcsin(2x) \right)$$
Soit :
$$\forall x \in \left[0 \,;\, \dfrac{1}{2} \right], \,\, \sqrt{\left( \sin \left( \arccos(x) \right) \right)^2 } = 2x$$
Soit encore :
$$\forall x \in \left[0 \,;\, \dfrac{1}{2} \right], \,\, \sqrt{1 - \left( \cos \left( \arccos(x) \right) \right)^2 } = 2x$$
Ce qui nous donne :
$$\forall x \in \left[0 \,;\, \dfrac{1}{2} \right], \,\, \sqrt{1 - \left( x\right)^2 } = 2x$$
Ceci implique que :
$$\forall x \in \left[0 \,;\, \dfrac{1}{2} \right], \,\, 1 - x^2 = 4x^2$$
On a alors :
$$\forall x \in \left[0 \,;\, \dfrac{1}{2} \right], \,\, 1 = 5x^2$$
De fait :
$$\forall x \in \left[0 \,;\, \dfrac{1}{2} \right], \,\, \dfrac{1}{5} = x^2$$
La seule et unique valeur de $$x$$ à retenir est donc $$x = \sqrt{\dfrac{1}{5}} = \dfrac{1}{\sqrt{5}} \in \left[0 \,;\, \dfrac{1}{2} \right]$$.
En conclusion, l'équation $$E$$ admet une unique solution, à savoir :
$$\mathscr{S}_E = \left\lbrace \, \dfrac{1}{\sqrt{5}} \, \right\rbrace$$
Cette solution vaut approximativement $$\dfrac{1}{\sqrt{5}} \simeq 0,45$$. Ce résultat se vérifie graphiquement à l'aide d'un logiciel graphique. On a alors :
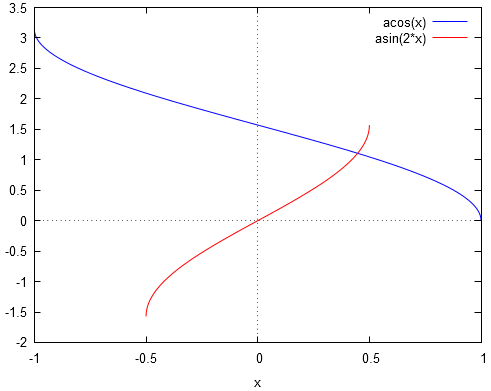Ceci confirme bien notre résultat trouvé.