Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 9 - Exercice 1
30 min
45
Une méthodologie bien pratique.
Question 1
-
On sait que si l'on cherche à exprimer la série de Fourier la fonction numérique, -périodique, dont l'image est, sur l'intervalle , donnée par l'expression , on trouve que :
Soit la fonction numérique , -périodique, dont l'image est, sur l'intervalle , donnée par l'expression . Déterminer l'expression de sa série de Fourier.
Soit la fonction numérique , -périodique, dont l'image est, sur l'intervalle , donnée par l'expression . Déterminer l'expression de sa série de Fourier.
Correction
L'énoncé suggère d'exploiter la relation proposée, à savoir :
Nous allons donc intégrer cette dernière relation entre les abscisses et . On a alors :
Ce qui nous donne :
Mais, on sait que et que :
Soit :
Ce qui nous conduit naturellement à :
Il nous faut maintenant expliciter la série de Fourier qui est associée au terme . Pour ce faire, nous effectuer, cette fois, une dérivation.
On a alors :
Soit :
Soit encore :
La dérivation s'effectuant par rapport à la variable , nous pouvons écrire que :
Avec et
Ce qui nous donne :
Nous allons donc écrire ceci comme :
En simplifiant par , non nul, on obtient :
Enfin, on sait que . Ce qui finalement nous donne :
On en déduit alors que :
Nous allons donc écrire que :
Soit :
Soit encore :
Donc :
En regroupant les deux sommations, on obtient :
En factorisant, on arrive à :
Finalement, on trouve que :
A titre informatif, on donne ci-dessous le graphe de la somme partielle :
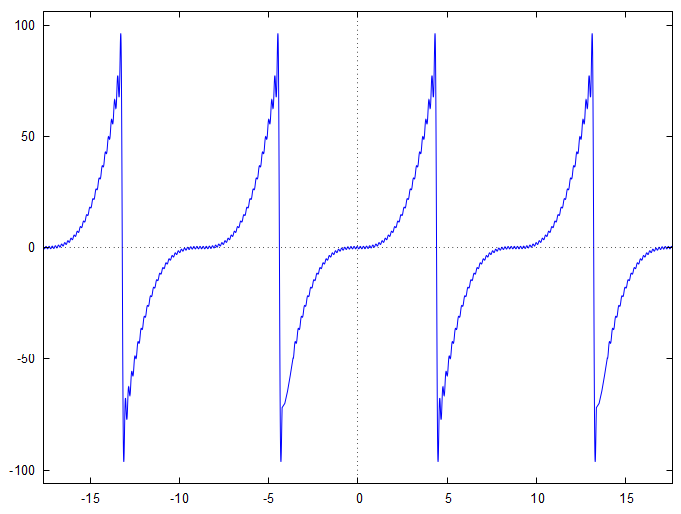
En allant jusqu'à le résultat est particulièrement convaincant.
Nous allons donc intégrer cette dernière relation entre les abscisses et . On a alors :
Ce qui nous donne :
Mais, on sait que et que :
Soit :
Ce qui nous conduit naturellement à :
Il nous faut maintenant expliciter la série de Fourier qui est associée au terme . Pour ce faire, nous effectuer, cette fois, une dérivation.
On a alors :
Soit :
Soit encore :
La dérivation s'effectuant par rapport à la variable , nous pouvons écrire que :
Avec et
Ce qui nous donne :
Nous allons donc écrire ceci comme :
En simplifiant par , non nul, on obtient :
Enfin, on sait que . Ce qui finalement nous donne :
On en déduit alors que :
Nous allons donc écrire que :
Soit :
Soit encore :
Donc :
En regroupant les deux sommations, on obtient :
En factorisant, on arrive à :
Finalement, on trouve que :
A titre informatif, on donne ci-dessous le graphe de la somme partielle :

En allant jusqu'à le résultat est particulièrement convaincant.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.