On note par
i le nombre complexe tel que
i2=−1.
Nous savons que pour une fonction numérique qui est
2L-périodique, on a l'expression suivante :
cn=2L1∫02Lf(x)e−iLnπxdxPour nous
2L=1 et
L=21. On a alors :
cn=11∫01e−xe−i2nπxdx=11∫01e−x+i2nπxdx=∫01e−(1+i2nπ)xdxOn a alors :
cn=[−1+i2nπe−(1+i2nπ)x]01=[1+i2nπe−(1+i2nπ)x]10=1+i2nπe−(1+i2nπ)0−e−(1+i2nπ)1=1+i2nπe0−e−(1+i2nπ)=1+i2nπ1−e−(1+i2nπ)En faisant usage de l'expression conjuguée, on obtient :
cn=1+i2nπ1−e−(1+i2nπ)×1−i2nπ1−i2nπ=1−4n2π2(1−e−(1+i2nπ))×(1−i2nπ)=1−4n2π2(1−e−1e−i2nπ)×(1−i2nπ)Soit :
cn=1−4n2π2(1−e−1(e−inπ)2)×(1−i2nπ)=1−4n2π2(1−e−1(−1)2)×(1−i2nπ)=1−4n2π2(1−e−1)×(1−i2nπ)Soit encore :
cn=1−4n2π21−e−1(1−i2nπ)De plus, on a :
1−4n2π21−e−1=1−4n2π21−e1=1−4n2π2ee−e1=1−4n2π2ee−1=e(1−4n2π2)e−1=−e(4n2π2−1)e−1 D'où :
cn=−e(4n2π2−1)e−1(1−i2nπ)En développant :
cn=−e(4n2π2−1)e−1+ie(4n2π2−1)2nπ(e−1)La série de Fourier prend donc la forme suivante :
SFf(x)=n=−∞∑+∞[−e(4n2π2−1)e−1+ie(4n2π2−1)2nπ(e−1)]e21inxEn factorisant :
SFf(x)=ee−1n=−∞∑+∞[−4n2π2−11+i4n2π2−12nπ]e2inxOu de manière équivalente :
SFf(x)=ee−1n=−∞∑+∞[4n2π2−1i2nπ−1]e2inxLa fonction
f étudiée ici satisfait aux condition de Dirichlet, cette série de Fourier converge bien et elle converge vers la régularisée
f⋆. D'où :
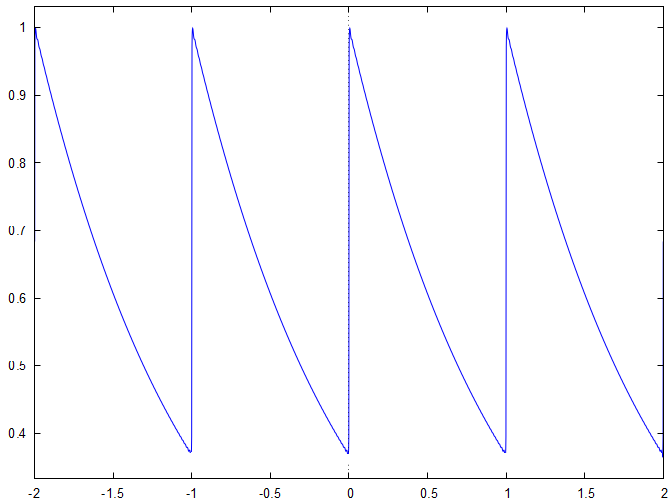
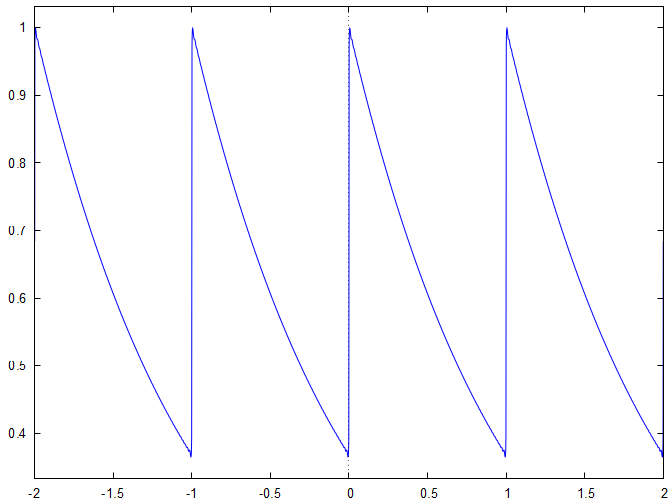
f⋆(x)=ee−1n=−∞∑+∞[4n2π2−1i2nπ−1]e2inx=ee−1n=−∞∑+∞[−4n2π2−11+i4n2π2−12nπ]e2inxLe graphe de la fonction étudié est :
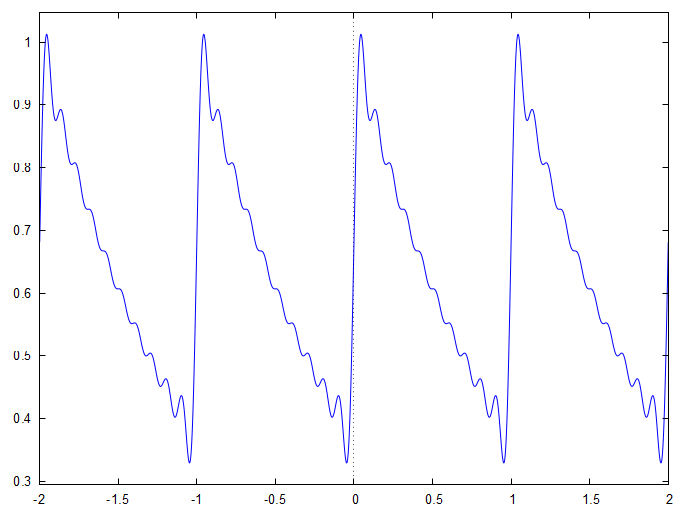
Lorsque nous traçons la somme partielle
ee−1n=−10∑10[4n2π2−1i2nπ−1]e2inx nous obtenons :
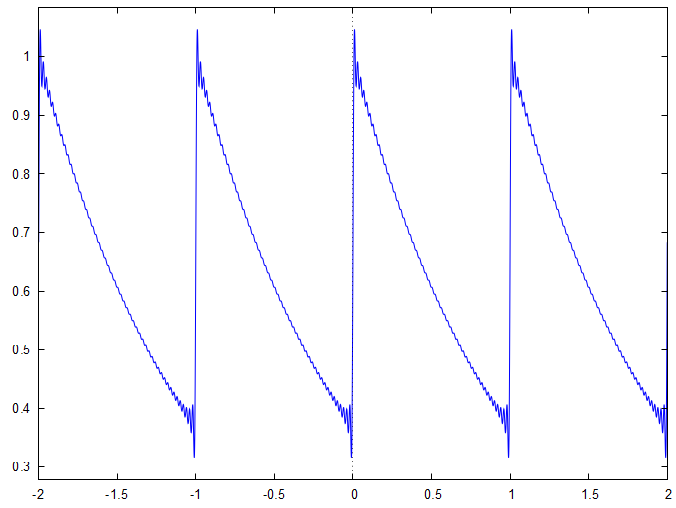
Puis, lorsque nous traçons la somme partielle
ee−1n=−50∑50[4n2π2−1i2nπ−1]e2inx nous obtenons :
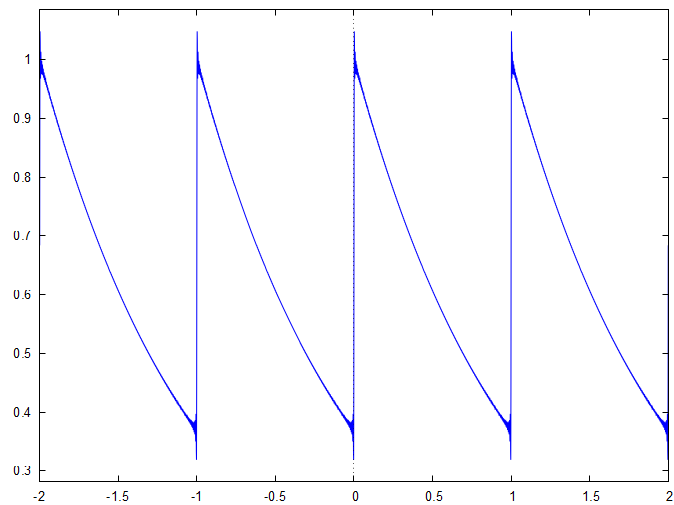
Ensuite lorsque nous traçons la somme partielle
ee−1n=−200∑200[4n2π2−1i2nπ−1]e2inx nous obtenons :
Enfin, en passant jusqu'à la somme partielle
ee−1n=−200∑200[4n2π2−1i2nπ−1]e2inx nous obtenons :
On constate bien la convergence de la série de Fourier ainsi que la puissance de ce formalisme.