Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 6 - Exercice 1
40 min
60
De l'entrainement, toujours de l'entrainement et du sens Physique (électronique) !
Question 1
-
Soit une constante réelle strictement positive. On pose alors :
Déterminer la série de Fourier associée à .
REMARQUE :
, si une telle fonction décrit un courant électrique, alors on parle de . Ces courants redressés ont de nombreuses applications industrielles.
Déterminer la série de Fourier associée à .
REMARQUE :
, si une telle fonction décrit un courant électrique, alors on parle de . Ces courants redressés ont de nombreuses applications industrielles.
Correction
Soit une constante réelle strictement positive. On pose alors :
On constate que la présence de la valeur absolue modifie la périodicité . En effet, présente un redressement positif de toutes les parties négatives du graphe associé à .
A titre d'exemple, pour illustrer pleinement nos propos, choisissons , et ceci se traduit graphiquement par :
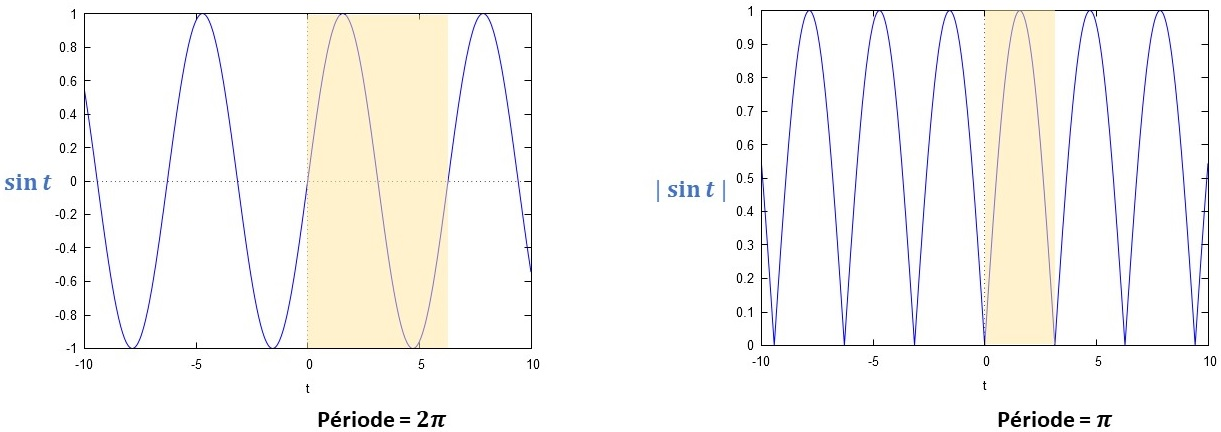
Donc, la période de l'expression est et on en déduit que la période du terme est donnée par .
La série de Fourier associée à nécessite la connaissance des trois coefficients réels , et .
L'expression est paire, donc les coefficients réels sont tous nuls, quelque soit la valeur de .
Le coefficient est quant à lui donné par :
Soit :
D'où :
Enfin, les coefficients réels se déterminent par l'intégrale suivante :
Or, on sait que :
Ainsi, on en déduit que :
Soit :
Soit encore :
La fonction sinus étant impaire, on en déduit alors que :
Ainsi, on peut écrire que :
Soit en intégrant :
Ce qui nous donne encore :
D'où :
Soit encore :
On obtient alors :
Ce qui nous donne au final :
La série de Fourier vas donc s'écrire comme :
Finalement :
On constate que la présence de la valeur absolue modifie la périodicité . En effet, présente un redressement positif de toutes les parties négatives du graphe associé à .
A titre d'exemple, pour illustrer pleinement nos propos, choisissons , et ceci se traduit graphiquement par :

Donc, la période de l'expression est et on en déduit que la période du terme est donnée par .
La série de Fourier associée à nécessite la connaissance des trois coefficients réels , et .
L'expression est paire, donc les coefficients réels sont tous nuls, quelque soit la valeur de .
Le coefficient est quant à lui donné par :
Soit :
D'où :
Enfin, les coefficients réels se déterminent par l'intégrale suivante :
Or, on sait que :
Ainsi, on en déduit que :
Soit :
Soit encore :
La fonction sinus étant impaire, on en déduit alors que :
Ainsi, on peut écrire que :
Soit en intégrant :
Ce qui nous donne encore :
D'où :
Soit encore :
On obtient alors :
Ce qui nous donne au final :
La série de Fourier vas donc s'écrire comme :
Finalement :
Question 2
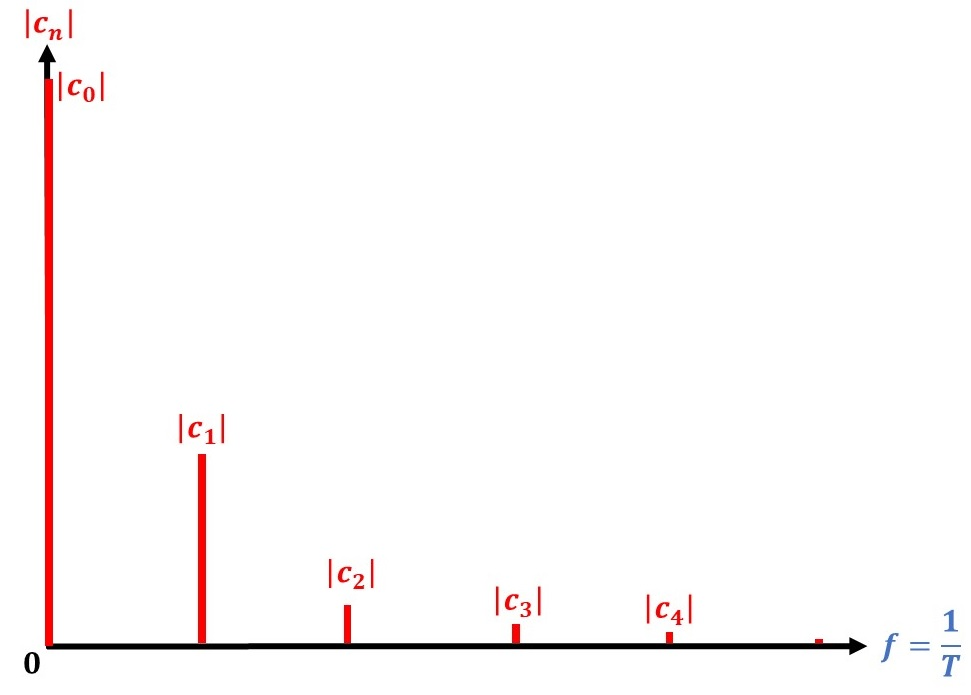
Le graphe des coefficients () s'appelle le spectre en amplitude (le graphe des coefficients s'appelle lui, le spectre énergétique). Comme cela signifie que .
Construire le spectre de .
Construire le spectre de .
Correction
On a, pour :
D'où le suivant :
;
;
;
;
...
D'où le graphique :
D'où le suivant :
;
;
;
;
...
D'où le graphique :

Question 3
On appelle taux d'harmonique, noté , d'un courant périodique, le rapport suivant :
Calculer ce coefficient pour notre signal. En proposer une interprétation.
Calculer ce coefficient pour notre signal. En proposer une interprétation.
Correction
Le , noté , d'un courant périodique, représente un rapport des puissances moyennes : celles de toutes les harmoniques à celle du fondamental. Il donne une mesure de l'importance relative des composantes harmoniques par rapport à celle du fondamental. Il permet donc, au sens de l'énergie, de comparer un courant périodique à un courant purement sinusoïdale (ou monochromatique). Et on a :
Le théorème de Parseval nous dit que :
Soit :
D'où :
Soit encore :
Avec :
D'où :
On obtient alors :
On peut donc écrire que :
Or, on sait que , d'où :
Finalement, on trouve que :
Le signal étudié, modélisé par est énergétiquement pur à .
Le théorème de Parseval nous dit que :
Soit :
D'où :
Soit encore :
Avec :
D'où :
On obtient alors :
On peut donc écrire que :
Or, on sait que , d'où :
Finalement, on trouve que :
Le signal étudié, modélisé par est énergétiquement pur à .
Question 4
On appelle , noté , d'un courant périodique, le rapport suivant :
Calculer ce coefficient pour notre signal. En proposer une interprétation.
Calculer ce coefficient pour notre signal. En proposer une interprétation.
Correction
Le , noté , d'un courant périodique est le rapport suivant :
Il représente le rapport de la puissance moyenne de la composante variable de (appelé courant d'ondulation) à celle de la valeur moyenne de . le taux d'ondulation permet de comparer le courant périodique au courant continu moyen.
On a :
Or, on sait que , ce qui implique que . On peut alors écrire que :
Ce qui nous permet d'écrire que :
Finalement, on trouve que :
La partie ondulante du signal étudié, modélisé par , représente de ce dernier.
Il représente le rapport de la puissance moyenne de la composante variable de (appelé courant d'ondulation) à celle de la valeur moyenne de . le taux d'ondulation permet de comparer le courant périodique au courant continu moyen.
On a :
Or, on sait que , ce qui implique que . On peut alors écrire que :
Ce qui nous permet d'écrire que :
Finalement, on trouve que :
La partie ondulante du signal étudié, modélisé par , représente de ce dernier.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.