Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 5 - Exercice 1
1 h 30 min
125
Une première application des séries de Fourier à la Physique.
Question 1
En Physique, tout signal temporel périodique ( en seconde), de période , est développable en série de Fourier :
ou est la pulsion propre du signal et . Les coefficients réels et portent le nom de coefficients de Fourier associés à . C'est deux coefficients réels sont donnés par les expressions suivantes :
Le terme s'appelle l' de rang .
En physique, un harmonique (c'est un nom masculin !) est l'élément de décomposition primaire d'une fonction périodique exprimé dans la base de Hilbert.
Démontrer que le coefficient réel représente la valeur moyenne temporelle, notée , du signal sur une période.
ou est la pulsion propre du signal et . Les coefficients réels et portent le nom de coefficients de Fourier associés à . C'est deux coefficients réels sont donnés par les expressions suivantes :
Le terme s'appelle l' de rang .
En physique, un harmonique (c'est un nom masculin !) est l'élément de décomposition primaire d'une fonction périodique exprimé dans la base de Hilbert.
Démontrer que le coefficient réel représente la valeur moyenne temporelle, notée , du signal sur une période.
Correction
La la valeur moyenne temporelle s'exprime comme :
Soit :
Comme la moyenne est un opérateur linéaire, on a :
Les coefficients , et étant des nombres réels, ils sont donc égaux à leur valeur moyenne. Ainsi, on a :
Avec :
Comme , on a :
Puis, on a également :
Comme , on a :
Donc, on a :
Ce qui nous permet d'obtenir :
Soit :
Comme la moyenne est un opérateur linéaire, on a :
Les coefficients , et étant des nombres réels, ils sont donc égaux à leur valeur moyenne. Ainsi, on a :
Avec :
Comme , on a :
Puis, on a également :
Comme , on a :
Donc, on a :
Ce qui nous permet d'obtenir :
Question 2
Dans tout ce qui suit, on choisit comme fonction l'intensité électrique du courant électrique circulant dans un circuit, dont la forme est représentée par :
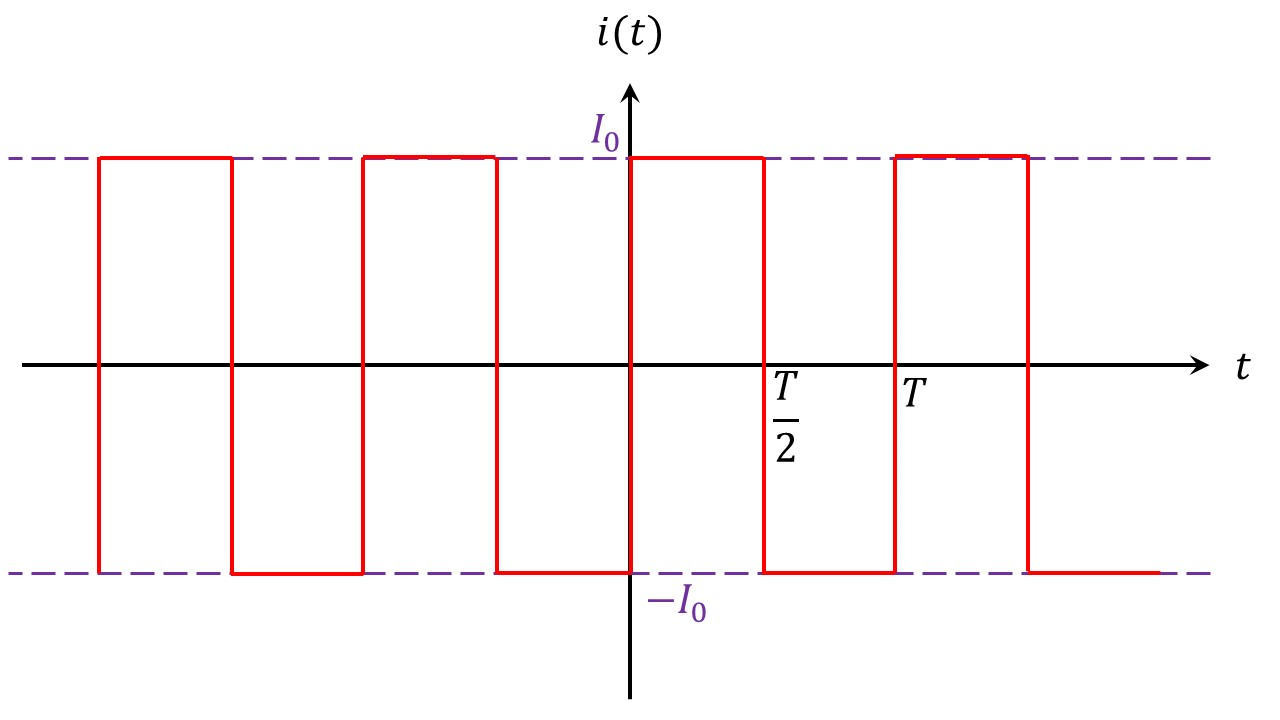
Déterminer par le calcul la valeur de de ce signal.

Déterminer par le calcul la valeur de de ce signal.
Correction
La valeur de de ce signal est donnée par :
Soit :
Ce qui nous donne :
Ainsi :
Soit :
Ce qui nous donne :
Ainsi :
Question 3
Calculer, , la valeur de .
Correction
On a, , la valeur suivante de :
Ce qui nous donne :
Soit :
Soit encore :
D'où :
Or, , d'où :
On a alors :
Finalement, , on a :
Ceci est normal, car la fonction est impaire.
Ce qui nous donne :
Soit :
Soit encore :
D'où :
Or, , d'où :
On a alors :
Finalement, , on a :
Ceci est normal, car la fonction est impaire.
Question 4
Calculer, , la valeur de uniquement en fonction de et .
Correction
On a, , l'expression de suivante :
Ce qui nous donne :
Soit :
Soit encore :
Ce qui nous donne :
Or, , d'où :
Ce qui nous donne :
Ainsi :
Finalement, , on obtient :
Ce qui nous donne :
Soit :
Soit encore :
Ce qui nous donne :
Or, , d'où :
Ce qui nous donne :
Ainsi :
Finalement, , on obtient :
Question 5
Démontrer que seuls les coefficients associés à des valeurs de impaires, donc de la forme (), sont non nuls.
Correction
Distinguons la parité de .
- si est pair alors dans ce cas, on pose avec .
Ainsi, on a :
- si est impair dans ce cas, on pose avec .
Ainsi, on a :
Soit :
- si est pair alors dans ce cas, on pose avec .
Ainsi, on a :
- si est impair dans ce cas, on pose avec .
Ainsi, on a :
Soit :
Question 6
Donner l'expression de en fonction de , , et .
Correction
L'expression de est alors :
En factorisant, on obtient :
En factorisant, on obtient :
Question 7
Exprimer l'expression des trois premières harmoniques non nulles, préciser leur rang, c'est-à-dire la valeur de l'entier associé.
Correction
On a :
Si c'est l'harmonique de rang :
Si c'est l'harmonique de rang :
Si c'est l'harmonique de rang :
Si c'est l'harmonique de rang :
Si c'est l'harmonique de rang :
Si c'est l'harmonique de rang :
Question 8
Déterminer l'expression du rapport . Penser à distinguer la parité de .
Correction
On a :
D'où, pour impair uniquement (soit avec ), on a :
Soit :
Dans le cas pair, on a immédiatement :
D'où, pour impair uniquement (soit avec ), on a :
Soit :
Dans le cas pair, on a immédiatement :
Question 9
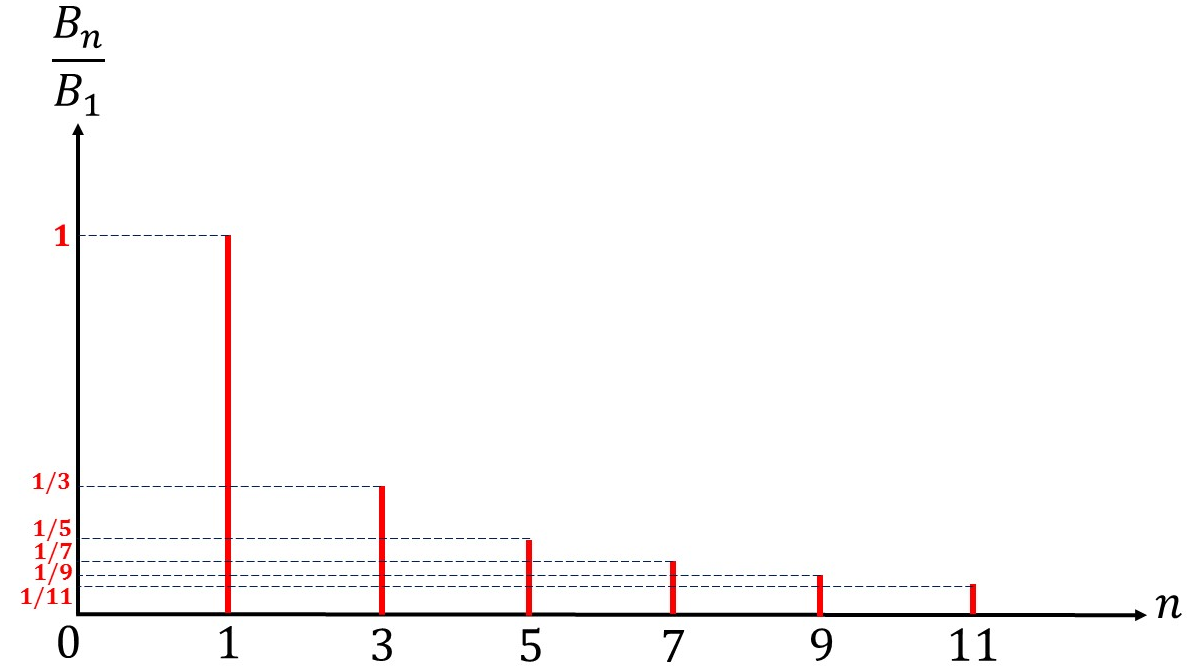
On appelle spectre en amplitudes relatives la représentation graphique du rapport en fonction de l'entier . Représenter graphiquement le spectre en amplitudes relatives. Vous représenterez les six premiers termes.
Correction
Le spectre renseigne sur la structure fréquentielle \og intime d'un signal \fg. C'est une technique très utilisé dans tous les domaines (Mathématiques, Physiques ou Ingénierie vibratoire) ou une description harmonique est utilisée.
L'analyse harmonique est la branche des Mathématiques qui étudie la représentation des fonctions ou des signaux comme superposition d'ondes de base. Elle approfondit et généralise les notions de série de Fourier et de transformée de Fourier.
Les ondes de base s'appellent les harmoniques, d'où le nom de la discipline. Durant ces deux derniers siècles, elle a eu de nombreuses applications en physiques sous le nom d'analyse spectrale, et connaît des applications récentes notamment en traitement des signaux, mécanique quantique, neurosciences, stratigraphie ... etc
Dans le cas de notre signal électrique , on a le spectre en amplitudes relatives suivant :
L'analyse harmonique est la branche des Mathématiques qui étudie la représentation des fonctions ou des signaux comme superposition d'ondes de base. Elle approfondit et généralise les notions de série de Fourier et de transformée de Fourier.
Les ondes de base s'appellent les harmoniques, d'où le nom de la discipline. Durant ces deux derniers siècles, elle a eu de nombreuses applications en physiques sous le nom d'analyse spectrale, et connaît des applications récentes notamment en traitement des signaux, mécanique quantique, neurosciences, stratigraphie ... etc
Dans le cas de notre signal électrique , on a le spectre en amplitudes relatives suivant :

Question 10
On appelle valeur efficace d'une fonction -périodique, notée , la valeur suivante :
Calculer la valeur efficace, notée , du signal en fonction des coefficients de Fourier.
Calculer la valeur efficace, notée , du signal en fonction des coefficients de Fourier.
Correction
La valeur efficace , du signal est donnée par :
Or, on a :
Ce qui nous donne :
On pose alors :
D'où :
Soit :
Avec :
Soit :
Et on a :
Soit :
Puis, on a :
Soit :
Comme et , on en déduit immédiatement que :
Ce qui implique que :
En factorisant, on obtient :
Finalement, on en déduit que :
Remarque :
Nous aurions pu obtenir directement cette relation en faisant usage de l'égalité de Parseval. En effet, l' égalité de Parseval nous apprend que :
Soit :
Or, on a :
Ce qui nous donne :
On pose alors :
D'où :
Soit :
Avec :
Soit :
Et on a :
Soit :
Puis, on a :
Soit :
Comme et , on en déduit immédiatement que :
Ce qui implique que :
En factorisant, on obtient :
Finalement, on en déduit que :
Remarque :
Nous aurions pu obtenir directement cette relation en faisant usage de l'égalité de Parseval. En effet, l' égalité de Parseval nous apprend que :
Soit :
Question 11
Calculer la valeur efficace de l'harmonique numéro .
Correction
La valeur efficace de l'harmonique numéro est donnée par l'expression suivante :
Comme , on obtient :
De plus, avec l'équation numérotée (53), on a :
Donc :
Finalement, on obtient :
Comme , on obtient :
De plus, avec l'équation numérotée (53), on a :
Donc :
Finalement, on obtient :
Question 12
Démontrer que .
Correction
On a :
Finalement, on en déduit que :
Finalement, on en déduit que :
Question 13
Démontrer, à partir de la forme du signal, que .
Correction
On a :
Ainsi, on obtient :
Soit :
Ce qui nous donne :
Finalement, comme , on a bien :
Ainsi, on obtient :
Soit :
Ce qui nous donne :
Finalement, comme , on a bien :
Question 14
En déduire la valeur exacte de la série suivante :
Correction
On a :
Soit :
Ce qui nous donne :
Ainsi, on obtient :
On en déduit immédiatement la valeur exacte de la série numérique suivante :
Soit :
Ce qui nous donne :
Ainsi, on obtient :
On en déduit immédiatement la valeur exacte de la série numérique suivante :
Question 15
On note par la valeur efficace de la série de Fourier associée à en limitant uniquement aux six premiers termes non nul. Déterminer la valeur du rapport suivant :
Quelle conclusion pouvez-vous faire ?
Quelle conclusion pouvez-vous faire ?
Correction
On a :
Soit :
Soit encore :
Mais comme , on en déduit donc que :
Donc, on trouve que :
Ce qui nous donne donc :
On peut ainsi conclure que la superposition des six premiers harmoniques suffit à reproduire à la valeur de . Ce qui est totalement suffisant (et satisfaisant) dans le cadre d'une expérience physique.
Soit :
Soit encore :
Mais comme , on en déduit donc que :
Donc, on trouve que :
Ce qui nous donne donc :
On peut ainsi conclure que la superposition des six premiers harmoniques suffit à reproduire à la valeur de . Ce qui est totalement suffisant (et satisfaisant) dans le cadre d'une expérience physique.
Question 16
Dans le cadre de notre signal étudié, déterminer la limite suivante :
Quelle interprétation physique pouvez-vous faire de ce résultat mathématique connu sous le nom de lemme de Riemann-Lebesgue.
Quelle interprétation physique pouvez-vous faire de ce résultat mathématique connu sous le nom de lemme de Riemann-Lebesgue.
Correction
Dans le cadre de notre signal étudié, on a la limite suivante :
Finalement, on trouve que :
Physiquement, ce résultat signifie que les harmoniques de faible rang participent davantage à la " reconstruction " du signal. Ceci se retrouve, de manière très visuelle, sur le spectre en amplitude relative. En effet, les hauteurs associées sont strictement décroissantes. Ceci justifie que le tout premier harmonique soit, par les physiciens, souvent appelé "le Fondamental".
Ainsi, les harmoniques de faibles rang sont les plus participatives à la physique associée à un signal. En Mathématiques, ce résultat est très général, et est historiquement connu sous le nom de lemme de Riemann-Lebesgue.
Dans le cadre des séries de Fourier c'est le mathématicien allemand Bernhard Riemann qui démontra ce résultat pour le première fois en 1854.
Finalement, on trouve que :
Physiquement, ce résultat signifie que les harmoniques de faible rang participent davantage à la " reconstruction " du signal. Ceci se retrouve, de manière très visuelle, sur le spectre en amplitude relative. En effet, les hauteurs associées sont strictement décroissantes. Ceci justifie que le tout premier harmonique soit, par les physiciens, souvent appelé "le Fondamental".
Ainsi, les harmoniques de faibles rang sont les plus participatives à la physique associée à un signal. En Mathématiques, ce résultat est très général, et est historiquement connu sous le nom de lemme de Riemann-Lebesgue.
Dans le cadre des séries de Fourier c'est le mathématicien allemand Bernhard Riemann qui démontra ce résultat pour le première fois en 1854.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.