Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Tchat avec un prof

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Exercice 15 - Exercice 1

3 h
240
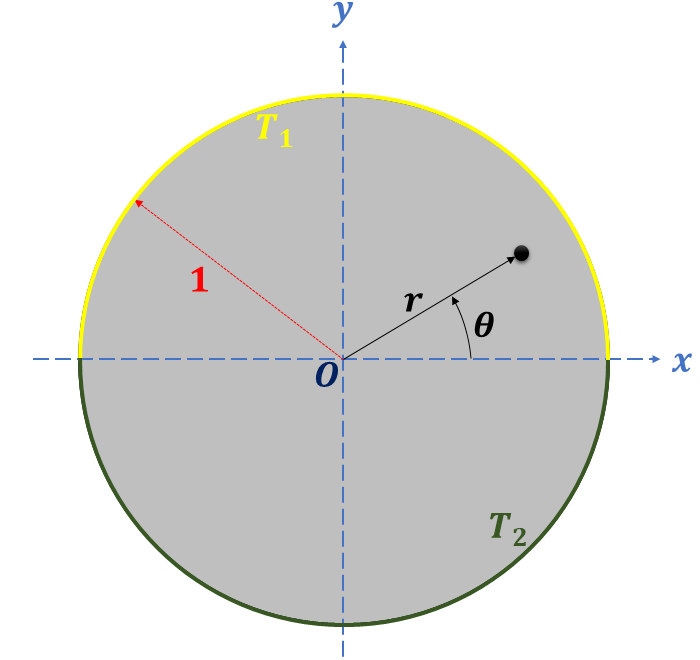
On considère une plaque circulaire métallique, homogène, linéaire et isotrope de rayon unité.
Expérimentalement, les faces de cette plaque sont isolées et on s'arrange pour que le contour supérieur soit à la température T1>0T_1 > 0 et le contour inférieur à la température T2>0T_2 > 0.
On note par rr et θ\theta, avec r∈[0 ; 1]r \in \left[ 0 \,;\,1 \right] et θ∈[0 ; 2π[\theta \in \left[ 0 \,;\,2\pi \right[, les coordonnées des points matériels (physiques) de cette plaque. Ceci se représente par la figure suivante par :

On note par TT la fonction température de cette plaque et on a :
T:{[0 ; 1]×[0 ; 2π[⟶R(r ; θ)⟼T(r ; θ)T : \left\lbrace \begin{array}{rcl} \left[ 0 \,;\,1 \right] \times \left[ 0 \,;\,2\pi \right[ & \longrightarrow & \mathbb{R} \\ & & \\ (r \,;\, \theta) & \longmapsto & T(r \,;\, \theta) \\ \end{array} \right.
Les conditions initiales de bord se traduisent par :
T(r=1 ; θ):{T1si0<θ<πT2siπ<θ<2πT(r=1 \,;\, \theta) : \left\lbrace \begin{array}{rcl} T_1 & \mathrm{si} & 0 < \theta < \pi \\ & & \\ T_2 & \mathrm{si} & \pi < \theta < 2\pi \\ \end{array} \right.
On laisse le temps à la plaque de voir sa température s'établir et devenir stationnaire. En ce sens la dépendance temporelle de la température n'est pas à prendre en compte. L'équation de la chaleur à résoudre est donc la suivante :
r2∂2T∂r2(r ; θ)+r∂T∂r(r ; θ)+∂2T∂θ2(r ; θ)=0r^2 \dfrac{\partial^2 T}{\partial r^2} \left( r \,;\, \theta \right) + r \dfrac{\partial T}{\partial r} \left( r \,;\, \theta \right) + \dfrac{\partial^2 T}{\partial \theta^2} \left( r \,;\, \theta \right) = 0
Bien évidemment, l'évolution de la température au sein de la plaque impose que la température est bornée (afin de s'assurer que la plaque ne soit pas détruite) de telle façon à pouvoir écrire que :
∀r∈[0 ; 1],  ∀θ∈[0 ; 2π[,   ∣ T(r ; θ) ∣<K  (K∈R+)\forall r \in \left[ 0 \,;\,1 \right], \,\, \forall \theta \in \left[ 0 \,;\,2\pi \right[, \,\,\, \left\vert \, T \left( r \,;\, \theta \right) \, \right\vert < K \,\, (K \in \mathbb{R}^+)
Les conditions et hypothèses, fixant le cadre de ce travail, permettent d'envisager l'écriture d'une solution, mathématiquement et physiquement acceptable, de la forme (dénommée aˋ variables seˊpareˊes{\color{blue}{\textit{à variables séparées}}} ) suivante :
T(r ; θ)=R(r)×Θ(θ)T\left( r \,;\, \theta \right) = R(r) \times \Theta(\theta)
Les termes RR et Θ\Theta désignent deux fonctions réelles, au moins deux de classe C2C^2 sur les intervalles considérés.
▶  \blacktriangleright \,\, Information Utile\textbf{Information Utile}
On donne la série suivante :
∑n=0+∞r2n+1sin⁡((2n+1)θ)2n+1=12arctan⁡(2rsin⁡(θ)1−r2)\sum_{n=0}^{+\infty} \dfrac{r^{2n+1} \sin\big( (2n+1) \theta \big)}{2n+1} = \dfrac{1}{2} \arctan\left( \dfrac{2r\sin(\theta)}{1-r^2} \right)
rsin⁡(θ)+r3sin⁡(3θ)3+r5sin⁡(5θ)5+r7sin⁡(7θ)7+⋯=12arctan⁡(2rsin⁡(θ)1−r2)r \sin\big( \theta \big) + \dfrac{r^3 \sin\big( 3 \theta \big)}{3} + \dfrac{r^5 \sin\big( 5 \theta \big)}{5} + \dfrac{r^7 \sin\big( 7 \theta \big)}{7} +\cdots = \dfrac{1}{2}\arctan\left( \dfrac{2r\sin(\theta)}{1-r^2} \right)
Question 1
Partie 1 - Eˊquation diffeˊrentielle d’Euler, cas de Cauchy{\color{RoyalBlue}{\textbf{Partie 1 - Équation différentielle d'Euler, cas de Cauchy}}}
Soit λ\lambda un nombre réel positif.
On considère l'équation différentielle lineˊaire{\color{red}{\textbf{linéaire}}}, notée (E)(\mathcal{E}) de type Euler et qui est référencée sous le nom de Cauchy, suivante
(E):   r2R′′(r)+rR′(r)−λ2R(r)=0(\mathcal{E}) : \,\,\, r^2 R''(r) + rR'(r) - \lambda^2 R(r) = 0
dans laquelle RR est la fonction que nous recherchons et de dépendance radiale symbolisée par la variable rr.

Soit kk un nombre réel. On recherche une solution simple{\color{blue}{\textbf{simple}}} à l'équation différentielle (E)(\mathcal{E}) de la forme R(r)=rkR(r) = r^k. Déterminer les valeurs de kk qui sont possibles.

Correction
Si R(r)=rkR(r) = r^k alors R′(r)=krk−1R'(r) = kr^{k-1} et R′′(r)=k(k−1)rk−2R''(r) = k(k-1)r^{k-2}. Donc on a :
(E):   r2k(k−1)rk−2+rkrk−1−λ2R(r)=0(\mathcal{E}) : \,\,\, r^2 k(k-1)r^{k-2} + r kr^{k-1} - \lambda^2 R(r) = 0
Ainsi :
(E):   k(k−1)rk+krk−λ2rk=0(\mathcal{E}) : \,\,\, k(k-1)r^{k} + kr^{k} - \lambda^2 r^k = 0
Soit :
(k(k−1)+k−λ2)rk=0\big( k(k-1)+ k - \lambda^2 \big) r^{k} = 0
Comme rkr^{k} ne peut-être toujours nul, on en déduit alors que :
k(k−1)+k−λ2=0   ⟺   k2−k+k−λ2=0   ⟺   k2−λ2=0   ⟺   k2=λ2k(k-1)+ k - \lambda^2 = 0 \,\,\, \Longleftrightarrow \,\,\, k^2 - k + k - \lambda^2 = 0 \,\,\, \Longleftrightarrow \,\,\, k^2 - \lambda^2 = 0 \,\,\, \Longleftrightarrow \,\,\, k^2 = \lambda^2
Donc les deux valeurs de kk qui sont possibles sont :
k=±λk = \pm \lambda
Question 2

Sachant que l'équation différentielle (E)(\mathcal{E}) est lineˊaire{\color{red}{\textbf{linéaire}}}, donner la solution générale R(r)R(r) recherchée.

Correction
Sachant que l'équation différentielle (E)(\mathcal{E}) est lineˊaire{\color{red}{\textbf{linéaire}}}, la solution générale R(r)R(r) recherchée est :
R(r)=A rλ+B r−λ     (A ; B)∈R2R(r) = A \, r^\lambda + B \, r^{-\lambda} \,\,\,\,\, (A\,;\,B)\in\mathbb{R}^2
Question 3

Dans le cas physique{\color{Magenta}{\textbf{physique}}} d'une fonction RR recherchée qui doit admettre en r=0r=0 une solution finie (c'est-à-dire non infinie), donc qui ne diverge pas aˋ l’origine{\color{Magenta}{\textbf{ne diverge pas à l'origine}}}, donner la solution de (E)(\mathcal{E}) qui soit physiquement acceptable.

Correction
Dans le cas physique{\color{Magenta}{\textbf{physique}}} d'une fonction RR recherchée qui doit admettre en r=0r=0 une solution finie (c'est-à-dire non infinie) on doit absolument avec B=0B=0 car le terme r−λr^{-\lambda} diverge à l'origine. De fait, on a :
R(r)=A rλ     A∈RR(r) = A \, r^\lambda \,\,\,\,\, A \in\mathbb{R}
Question 4
Partie 2 - Eˊquation diffeˊrentielle ordinaire{\color{RoyalBlue}{\textbf{Partie 2 - Équation différentielle ordinaire}}}
Soit λ\lambda un nombre réel positif.
On considère l'équation différentielle lineˊaire{\color{red}{\textbf{linéaire}}}, notée (H)(\mathcal{H}), suivante
(H):   Θ′′(θ)+λ2Θ(θ)=0(\mathcal{H}) : \,\,\, \Theta''(\theta) + \lambda^2 \Theta(\theta) = 0
dans laquelle Θ\Theta est la fonction que nous recherchons et de dépendance angulaire symbolisée par la variable θ\theta.

Sachant que l'équation différentielle (H)(\mathcal{H}) est lineˊaire{\color{red}{\textbf{linéaire}}}, donner la solution générale Θ(θ)\Theta(\theta) recherchée.

Correction
Sachant que l'équation différentielle (H)(\mathcal{H}) est lineˊaire{\color{red}{\textbf{linéaire}}} la solution générale Θ(θ)\Theta(\theta) recherchée est :
Θ(θ)=Ccos⁡(λθ)+Dsin⁡(λθ)     (C ; D)∈R2\Theta(\theta) = C \cos(\lambda \theta) + D \sin(\lambda \theta) \,\,\,\,\, (C\,;\,D)\in\mathbb{R}^2
Question 5

En outre, pour être physiquement acceptable{\color{Magenta}{\textbf{physiquement acceptable}}}, la fonction Θ\Theta doit être 2π2\pi-périodique et de classe C∞C^\infty sur R\mathbb{R}. Déterminer les valeurs possibles de λ\lambda.

Correction
En outre, pour être physiquement acceptable{\color{Magenta}{\textbf{physiquement acceptable}}}, la fonction Θ\Theta doit être 2π2\pi-périodique et de classe C∞C^\infty sur R\mathbb{R}. Donc λ\lambda doit être un nombre entier naturel. Ainsi :
λ=m∈N\lambda = m \in \mathbb{N}
Et de fait :
Θ(θ)=Ccos⁡(mθ)+Dsin⁡(mθ)     (m∈N ; (C ; D)∈R2)\Theta(\theta) = C \cos(m \theta) + D \sin(m \theta) \,\,\,\,\, \big( m \in \mathbb{N} \,;\, (C\,;\,D)\in\mathbb{R}^2 \big)
Question 6

Dans la littérature scientifique, comment est appelée l'équation différentielle lineˊaire{\color{red}{\textbf{linéaire}}} (H)(\mathcal{H}) ?

Correction
Dans la littérature scientifique, l'équation différentielle lineˊaire{\color{red}{\textbf{linéaire}}} (H)(\mathcal{H}) est connue sous le nom d'eˊquation diffeˊrentielle d’un oscillateur harmonique\textbf{équation différentielle d'un oscillateur harmonique}.
Question 7
Partie 3 - Solution aˋ notre probleˋme thermique de plaque{\color{RoyalBlue}{\textbf{Partie 3 - Solution à notre problème thermique de plaque}}}
On considère maintenant l'équation de la chaleur à résoudre :
r2∂2T∂r2(r ; θ)+r∂T∂r(r ; θ)+∂2T∂θ2(r ; θ)=0r^2 \dfrac{\partial^2 T}{\partial r^2} \left( r \,;\, \theta \right) + r \dfrac{\partial T}{\partial r} \left( r \,;\, \theta \right) + \dfrac{\partial^2 T}{\partial \theta^2} \left( r \,;\, \theta \right) = 0
On envisage l'écriture d'une solution de la forme aˋ variables seˊpareˊes{\color{blue}{\textit{à variables séparées}}} suivante :
T(r ; θ)=R(r)×Θ(θ)T\left( r \,;\, \theta \right) = R(r) \times \Theta(\theta)

Déterminer l'équation différentielle satisfaite par la fonction radiale RR.

Correction
On a T(r ; θ)=R(r)×Θ(θ)T\left( r \,;\, \theta \right) = R(r) \times \Theta(\theta). Donc on a :
r2Θ(θ)∂2R∂r2(r)+rΘ(θ)∂R∂r(r)+R(r)∂2Θ∂θ2(θ)=0r^2 \Theta(\theta) \dfrac{\partial^2 R}{\partial r^2}( r ) + r \Theta(\theta) \dfrac{\partial R}{\partial r} (r) + R(r) \dfrac{\partial^2 \Theta}{\partial \theta^2} ( \theta ) = 0
Divisons cette équation par R(r)×Θ(θ)R(r) \times \Theta(\theta). On obtient donc :
r2Θ(θ)R(r)×Θ(θ)∂2R∂r2(r)+rΘ(θ)R(r)×Θ(θ)∂R∂r(r)+R(r)R(r)×Θ(θ)∂2Θ∂θ2(θ)=0R(r)×Θ(θ)r^2 \dfrac{\Theta(\theta)}{R(r) \times \Theta(\theta)} \dfrac{\partial^2 R}{\partial r^2}( r ) + r \dfrac{\Theta(\theta)}{R(r) \times \Theta(\theta)} \dfrac{\partial R}{\partial r} (r) + \dfrac{R(r)}{R(r) \times \Theta(\theta)} \dfrac{\partial^2 \Theta}{\partial \theta^2} ( \theta ) = \dfrac{0}{R(r) \times \Theta(\theta)}
En simplifiant :
r21R(r)∂2R∂r2(r)+r1R(r)∂R∂r(r)+1Θ(θ)∂2Θ∂θ2(θ)=0r^2 \dfrac{1}{R(r)} \dfrac{\partial^2 R}{\partial r^2}( r ) + r \dfrac{1}{R(r)} \dfrac{\partial R}{\partial r} (r) + \dfrac{1}{\Theta(\theta)} \dfrac{\partial^2 \Theta}{\partial \theta^2} ( \theta ) = 0
Soit encore :
r21R(r)∂2R∂r2(r)+r1R(r)∂R∂r(r)=−1Θ(θ)∂2Θ∂θ2(θ)r^2 \dfrac{1}{R(r)} \dfrac{\partial^2 R}{\partial r^2}( r ) + r \dfrac{1}{R(r)} \dfrac{\partial R}{\partial r} (r) = - \dfrac{1}{\Theta(\theta)} \dfrac{\partial^2 \Theta}{\partial \theta^2} ( \theta )
Les deux membres de cette dernière égalités dépendent de variabilités différentes. La seule possibilité est que chaque membre soit égale à une même constante scalaire k∈Rk \in \mathbb{R}.
Afin de retrouver l'équation de Cauchy, on va poser k=−λ2⩽0k = -\lambda^2 \leqslant 0. De sorte que :
r21R(r)∂2R∂r2(r)+r1R(r)∂R∂r(r)=−λ2r^2 \dfrac{1}{R(r)} \dfrac{\partial^2 R}{\partial r^2}( r ) + r \dfrac{1}{R(r)} \dfrac{\partial R}{\partial r} (r) = - \lambda^2
Ainsi en multipliant par R(r)R(r) on obtient :
r2∂2R∂r2(r)+r∂R∂r(r)=−λ2R(r)r^2 \dfrac{\partial^2 R}{\partial r^2}( r ) + r \dfrac{\partial R}{\partial r} (r) = - \lambda^2 R(r)
Finalement, en remarquant que toute la dépendance de cette équation est purement radiale;, on obtient l'équation recherchée :
r2d2Rdr2(r)+rdRdr(r)+λ2R(r)=0r^2 \dfrac{d^2 R}{d r^2}( r ) + r \dfrac{d R}{d r} (r) + \lambda^2 R(r) = 0
Question 8

Donner la forme de la solution R(r)R(r) qui soit en accord avec nos hypothèses de travail.

Correction
D'après la première partie de cette épreuve, la forme de la solution R(r)R(r) qui soit en accord avec nos hypothèses de travail, qui impliquent λ=m∈N\lambda = m \in \mathbb{N}, est :
R(r)=A rm     (m∈N ; A∈R)R(r) = A \, r^m \,\,\,\,\, \big( m \in \mathbb{N} \,;\, A \in\mathbb{R} \big)
Question 9

Déterminer l'équation différentielle satisfaite par la fonction angulaire Θ\Theta.

Correction
On a donc :
λ2=−1Θ(θ)∂2Θ∂θ2(θ)\lambda^2 = - \dfrac{1}{\Theta(\theta)} \dfrac{\partial^2 \Theta}{\partial \theta^2} ( \theta )
Ce qui nous donne :
λ2Θ(θ)=−∂2Θ∂θ2(θ)\lambda^2 \Theta(\theta) = - \dfrac{\partial^2 \Theta}{\partial \theta^2} ( \theta )
L'équation différentielle satisfaite par la fonction angulaire Θ\Theta est :
∂2Θ∂θ2(θ)+λ2Θ(θ)=0\dfrac{\partial^2 \Theta}{\partial \theta^2} ( \theta ) + \lambda^2 \Theta(\theta) = 0
En observant que l'unique variabilité de cette équation est angulaire, on en déduit finalement que :
d2Θdθ2(θ)+λ2Θ(θ)=0\dfrac{d^2 \Theta}{d \theta^2} ( \theta ) + \lambda^2 \Theta(\theta) = 0
Question 10

Donner la forme de la solution Θ(θ)\Theta(\theta) qui soit en accord avec nos hypothèses de travail.

Correction
D'après ce qui précèdent la forme de la solution Θ(θ)\Theta(\theta) qui soit en accord avec nos hypothèses de travail est :
Θ(θ)=Ccos⁡(mθ)+Dsin⁡(mθ)     (m∈N ; (C ; D)∈R2)\Theta(\theta) = C \cos(m \theta) + D \sin(m \theta) \,\,\,\,\, \big( m \in \mathbb{N} \,;\, (C\,;\,D) \in\mathbb{R}^2 \big)
Question 11

Donner la forme de la solution T(r ; θ)T\left( r \,;\, \theta \right).

Correction
La forme de la solution T(r ; θ)T\left( r \,;\, \theta \right) est donc la suivante :
T(r ; θ)=R(r)×Θ(θ)T\left( r \,;\, \theta \right) = R(r) \times \Theta(\theta)
Soit :
T(r ; θ)=A rm×(Ccos⁡(mθ)+Dsin⁡(mθ))T\left( r \,;\, \theta \right) = A \, r^m \times \big( C \cos(m \theta) + D \sin(m \theta) \big)
Comme AA, CC et DD sont des constantes réelles, on a donc :
T(r ; θ)=rm×(Acos⁡(mθ)+Bsin⁡(mθ))T\left( r \,;\, \theta \right) = r^m \times \big( \mathcal{A} \cos(m \theta) + \mathcal{B} \sin(m \theta) \big)
Dans cette relation on a posé A=AC∈R\mathcal{A} = AC \in \mathbb{R} et B=AD∈R\mathcal{B} = AD \in \mathbb{R}.
Question 12

Par linéarité, nous envisagerons d'écrire la solution TT de notre problème de thermique de la plaque comme étant une superposition (ou combinaison) linéaire, sur toutes les valeurs possibles{\color{red}{\textbf{toutes les valeurs possibles}}} du nombre λ\lambda, de la forme solution de la question précédente. Écrire explicitement la forme solution mathématique ainsi obtenue.

Correction
Par linéarité, nous pouvons écrire que la forme solution mathématique ainsi obtenue est donnée par :
T(r ; θ)=∑m=0+∞(rm×(Amcos⁡(mθ)+Bmsin⁡(mθ)))T\left( r \,;\, \theta \right) = \sum_{m=0}^{+\infty} \left( r^m \times \big( \mathcal{A}_m \cos(m \theta) + \mathcal{B_m} \sin(m \theta) \big) \right)
Dans le but de faire apparaître dans la suite des développements une Série de Fourier, distinguons le cas m=0m=0 du cas m≠0m \neq 0.
T(r ; θ)=r0×(A0cos⁡(0θ)+B0sin⁡(0θ))+∑m=1+∞(rm×(Amcos⁡(mθ)+Bmsin⁡(mθ)))T\left( r \,;\, \theta \right) = r^0 \times \big( \mathcal{A}_0 \cos(0 \theta) + \mathcal{B_0} \sin(0 \theta) \big) + \sum_{m=1}^{+\infty} \left( r^m \times \big( \mathcal{A}_m \cos(m \theta) + \mathcal{B}_m \sin(m \theta) \big) \right)
Ce qui nous donne :
T(r ; θ)=1×(A0×1+B0×0)+∑m=1+∞(rm×(Amcos⁡(mθ)+Bmsin⁡(mθ)))T\left( r \,;\, \theta \right) = 1 \times \big( \mathcal{A}_0 \times 1 + \mathcal{B_0} \times 0 \big) + \sum_{m=1}^{+\infty} \left( r^m \times \big( \mathcal{A}_m \cos(m \theta) + \mathcal{B}_m \sin(m \theta) \big) \right)
Soit :
T(r ; θ)=A0+∑m=1+∞(rm×(Amcos⁡(mθ)+Bmsin⁡(mθ)))T\left( r \,;\, \theta \right) = \mathcal{A}_0 + \sum_{m=1}^{+\infty} \left( r^m \times \big( \mathcal{A}_m \cos(m \theta) + \mathcal{B}_m \sin(m \theta) \big) \right)
Que nous allons préféré écrire comme :
T(r ; θ)=2A02+∑m=1+∞(rm×(Amcos⁡(mθ)+Bmsin⁡(mθ)))T\left( r \,;\, \theta \right) = \dfrac{2\mathcal{A}_0}{2} + \sum_{m=1}^{+\infty} \left( r^m \times \big( \mathcal{A}_m \cos(m \theta) + \mathcal{B}_m \sin(m \theta) \big) \right)
Et finalement :
T(r ; θ)=a02+∑m=1+∞(rm×(Amcos⁡(mθ)+Bmsin⁡(mθ)))T\left( r \,;\, \theta \right) = \dfrac{a_0}{2} + \sum_{m=1}^{+\infty} \left( r^m \times \big( \mathcal{A}_m \cos(m \theta) + \mathcal{B}_m \sin(m \theta) \big) \right)
Dans cette relation le terme a0a_0 est une constante réelle et pour tout m∈N⋆m \in \mathbb{N}^\star les quantités Am\mathcal{A}_m et Bm\mathcal{B}_m sont des nombres réels qu'ils nous faudra déterminer.
Question 13

En écrivant la solution de la question précédente pour r=1r = 1, c'est-à-dire en écrivant formellement T(r=1 ; θ){\color{Indigo}{T(r=1 \,;\, \theta)}}, faites clairement apparaître une seˊrie de Fourier{\color{Indigo}{\textbf{une série de Fourier}}}, à savoir une forme du type :
T(r=1 ; θ)=a02+∑m=1+∞(am cos⁡(mθ)+bm sin⁡(mθ))T(r=1 \,;\, \theta) = \dfrac{a_0}{2} + \sum_{m=1}^{+\infty} \big( a_m \, \cos(m \theta) + b_m \, \sin(m \theta) \big)
Dans cette relation a0a_0 est un réel et, pour tout nombre entier naturel mm non nul, les termes ama_m et bmb_m désignent des quantités réelles.

Correction
En écrivant la solution de la question précédente pour r=1r = 1on obtient une forme du type :
T(r=1 ; θ)=a02+∑m=1+∞(am cos⁡(mθ)+bm sin⁡(mθ))T(r=1 \,;\, \theta) = \dfrac{a_0}{2} + \sum_{m=1}^{+\infty} \big( a_m \, \cos(m \theta) + b_m \, \sin(m \theta) \big)
Avec, pour tout m∈N⋆m \in \mathbb{N}^\star, am=Ama_m = \mathcal{A}_m et bm=Bmb_m = \mathcal{B}_m.
Question 14

Déterminer l'expression (simple) de a0a_0 en fonction de T1T_1 et T2T_2.

Correction
L'expression de a0a_0 est donnée par :
a0=1π∫02πT(r=1 ; θ)dθa_0 = \dfrac{1}{\pi} \int_{0}^{2\pi} T(r=1 \,;\, \theta) d\theta
Soit :
a0=1π(∫0πT1dθ+∫π2πT2dθ)a_0 = \dfrac{1}{\pi} \left( \int_{0}^{\pi} T_1 d\theta + \int_{\pi}^{2\pi} T_2 d\theta \right)
Soit encore :
a0=1π(T1∫0π1dθ+T2∫π2π1dθ)a_0 = \dfrac{1}{\pi} \left( T_1 \int_{0}^{\pi} 1 d\theta + T_2 \int_{\pi}^{2\pi} 1 d\theta \right)
Ce qui nous donne :
a0=1π(T1π+T2π)a_0 = \dfrac{1}{\pi} \left( T_1 \pi + T_2 \pi \right)
Ainsi :
a0=ππ(T1+T2)a_0 = \dfrac{\pi}{\pi} \left( T_1 + T_2 \right)
En simplifiant, on, obtient finalement :
a0=T1+T2a_0 = T_1 + T_2
Question 15

Soit m∈N⋆m \in \mathbb{N}^\star. Déterminer l'expression (simple) de ama_m.

Correction
Soit m∈N⋆m \in \mathbb{N}^\star. L'expression de ama_m est :
am=1π∫02πT(r=1 ; θ)cos⁡(mθ)dθa_m = \dfrac{1}{\pi} \int_{0}^{2\pi} T(r=1 \,;\, \theta) \cos(m \theta) d\theta
Soit :
am=1π(∫0πT1cos⁡(mθ)dθ+∫π2πT2cos⁡(mθ)dθ)a_m = \dfrac{1}{\pi} \left( \int_{0}^{\pi} T_1 \cos(m \theta) d\theta + \int_{\pi}^{2\pi} T_2 \cos(m \theta) d\theta \right)
Soit encore :
am=1π(T1∫0πcos⁡(mθ)dθ+T2∫π2πcos⁡(mθ)dθ)a_m = \dfrac{1}{\pi} \left( T_1 \int_{0}^{\pi} \cos(m \theta) d\theta + T_2 \int_{\pi}^{2\pi} \cos(m \theta) d\theta \right)
Ce qui nous donne :
am=1mπ(T1[sin⁡(mθ)]0π+T2[sin⁡(mθ)]π2π)a_m = \dfrac{1}{m\pi} \left( T_1 \left[ \sin(m \theta) \right]_{0}^{\pi} + T_2 \left[ \sin(m \theta) \right]_{\pi}^{2\pi} \right)
Finalement, on trouve que
am=0a_m = 0
Question 16

Soit m∈N⋆m \in \mathbb{N}^\star. Déterminer l'expression générale de bmb_m en fonction de mm, π\pi, T1T_1 et T2T_2.

Correction
Soit m∈N⋆m \in \mathbb{N}^\star. L'expression générale de bmb_m est donnée par :
bm=1π∫02πT(r=1 ; θ)sin⁡(mθ)dθb_m = \dfrac{1}{\pi} \int_{0}^{2\pi} T(r=1 \,;\, \theta) \sin(m \theta) d\theta
Soit :
bm=1π(∫0πT1sin⁡(mθ)dθ+∫π2πT2sin⁡(mθ)dθ)b_m = \dfrac{1}{\pi} \left( \int_{0}^{\pi} T_1 \sin(m \theta) d\theta + \int_{\pi}^{2\pi} T_2 \sin(m \theta) d\theta \right)
Soit encore :
bm=1π(T1∫0πsin⁡(mθ)dθ+T2∫π2πsin⁡(mθ)dθ)b_m = \dfrac{1}{\pi} \left( T_1 \int_{0}^{\pi} \sin(m \theta) d\theta + T_2 \int_{\pi}^{2\pi} \sin(m \theta) d\theta \right)
Ce qui nous donne :
bm=−1mπ(T1[cos⁡(mθ)]0π+T2[cos⁡(mθ)]π2π)b_m = -\dfrac{1}{m\pi} \left( T_1 \left[ \cos(m \theta) \right]_{0}^{\pi} + T_2 \left[ \cos(m \theta) \right]_{\pi}^{2\pi} \right)
Ainsi :
bm=−1mπ(T1(cos⁡(mπ)−1)+T2(1−cos⁡(mπ)))b_m = -\dfrac{1}{m\pi} \left( T_1 \left( \cos(m \pi) -1 \right) + T_2 \left( 1 - \cos(m \pi) \right) \right)
De fait :
bm=−1mπ(−T1(1−cos⁡(mπ))+T2(1−cos⁡(mπ)))b_m = -\dfrac{1}{m\pi} \left( -T_1 \left( 1- \cos(m \pi) \right) + T_2 \left( 1 - \cos(m \pi) \right) \right)
Ce qui nous permet d'écrire que :
bm=1mπ(T1(1−cos⁡(mπ))−T2(1−cos⁡(mπ)))b_m = \dfrac{1}{m\pi} \left( T_1 \left( 1- \cos(m \pi) \right) - T_2 \left( 1 - \cos(m \pi) \right) \right)
En factorisant :
bm=T1−T2mπ(1−cos⁡(mπ))b_m = \dfrac{T_1-T_2}{m\pi} \left( 1 - \cos(m \pi) \right)
Donc :
bm=T1−T2mπ(1−(−1)m)b_m = \dfrac{T_1-T_2}{m\pi} \left( 1 - (-1)^m \right)
Question 17

On se place maintenant dans la situation des nombres{\color{blue}{\textbf{des nombres}}} m{\color{blue}{m}} pairs{\color{blue}{\textbf{pairs}}}. Dans ce cas précis, donner l'expression du terme bmb_m.

Correction
Si mm est pair donc de la forme m=2pm=2p, avec p∈N⋆p \in \mathbb{N}\star, alors on a :
(−1)m=(−1)2p=((−1)2)p=(1)p=1(-1)^m = (-1)^{2p} = \big( (-1)^2 \big)^p = (1)^p = 1
Et on en déduit que :
b2p=0b_{2p} = 0
Question 18

On se place maintenant dans la situation des nombres{\color{blue}{\textbf{des nombres}}} m{\color{blue}{m}} impairs{\color{blue}{\textbf{impairs}}}. Dans ce cas précis, donner l'expression du terme bmb_m.

Correction
Si mm est impair donc de la forme m=2p+1m=2p+1, avec p∈Np \in \mathbb{N}, alors on a :
(−1)m=(−1)2p+1=(−1)×(−1)2p=−1×1=−1(-1)^m = (-1)^{2p+1} = (-1) \times (-1)^{2p} = -1 \times 1 = -1
Et on en déduit que :
b2p+1=T1−T2(2p+1)π(1−(−1))b_{2p+1} = \dfrac{T_1-T_2}{(2p+1)\pi} \left( 1 - (-1) \right)
Donc :
b2p+1=2(T1−T2)(2p+1)πb_{2p+1} = \dfrac{2(T_1-T_2)}{(2p+1)\pi}
Question 19

Démontrer alors que :
T(r ; θ)=T1+T22+T1−T2πarctan⁡(2rsin⁡(θ)1−r2)T(r \,;\, \theta) = \dfrac{T_1 + T_2}{2} + \dfrac{T_1 - T_2}{\pi} \arctan\left( \dfrac{2r\sin(\theta)}{1-r^2} \right)

Correction
On a alors :
T(r ; θ)=T1+T22+∑m=1+∞(rm×(0cos⁡(mθ)+T1−T2mπ(1−(−1)m)sin⁡(mθ)))T\left( r \,;\, \theta \right) = \dfrac{T_1+T_2}{2} + \sum_{m=1}^{+\infty} \left( r^m \times \big( 0 \cos(m \theta) + \dfrac{T_1-T_2}{m\pi} \left( 1 - (-1)^m \right) \sin(m \theta) \big) \right)
Ce qui nous donne, en tenant compte uniquement des contributions impaires, la relation suivante :
T(r ; θ)=T1+T22+∑p=0+∞(r2p+12(T1−T2)(2p+1)πsin⁡((2p+1)θ))T\left( r \,;\, \theta \right) = \dfrac{T_1+T_2}{2} + \sum_{p=0}^{+\infty} \left( r^{2p+1} \dfrac{2(T_1-T_2)}{(2p+1)\pi} \sin((2p+1) \theta) \right)
Soit encore :
T(r ; θ)=T1+T22+2(T1−T2)π∑p=0+∞(r2p+112p+1sin⁡((2p+1)θ))T\left( r \,;\, \theta \right) = \dfrac{T_1+T_2}{2} + \dfrac{2(T_1-T_2)}{\pi}\sum_{p=0}^{+\infty} \left( r^{2p+1} \dfrac{1}{2p+1} \sin\big((2p+1) \theta\big) \right)
D'où :
T(r ; θ)=T1+T22+2T1−T2π∑p=0+∞(r2p+12p+1sin⁡((2p+1)θ))T\left( r \,;\, \theta \right) = \dfrac{T_1+T_2}{2} + 2\dfrac{T_1-T_2}{\pi}\sum_{p=0}^{+\infty} \left( \dfrac{r^{2p+1}}{2p+1} \sin\big((2p+1) \theta\big) \right)
Or, le sujet nous apprend que :
∑p=0+∞(r2p+12p+1sin⁡((2p+1)θ))=12arctan⁡(2rsin⁡(θ)1−r2)\sum_{p=0}^{+\infty} \left( \dfrac{r^{2p+1}}{2p+1} \sin \big( (2p+1) \theta \big) \right) = \dfrac{1}{2} \arctan\left( \dfrac{2r\sin(\theta)}{1-r^2} \right)
Ce qui nous permet d'écrire que :
T(r ; θ)=T1+T22+2T1−T2π12arctan⁡(2rsin⁡(θ)1−r2)T\left( r \,;\, \theta \right) = \dfrac{T_1+T_2}{2} + 2\dfrac{T_1-T_2}{\pi} \dfrac{1}{2} \arctan\left( \dfrac{2r\sin(\theta)}{1-r^2} \right)
Finalement, on a bien démontré que :
T(r ; θ)=T1+T22+T1−T2πarctan⁡(2rsin⁡(θ)1−r2)T(r \,;\, \theta) = \dfrac{T_1 + T_2}{2} + \dfrac{T_1 - T_2}{\pi} \arctan\left( \dfrac{2r\sin(\theta)}{1-r^2} \right)
Question 20

On se place dans le cas particulier pour lequel T1=2T_1 = 2 et T2=1T_2=1. Voici deux propositions de surface de température pour la plaque étudiée :

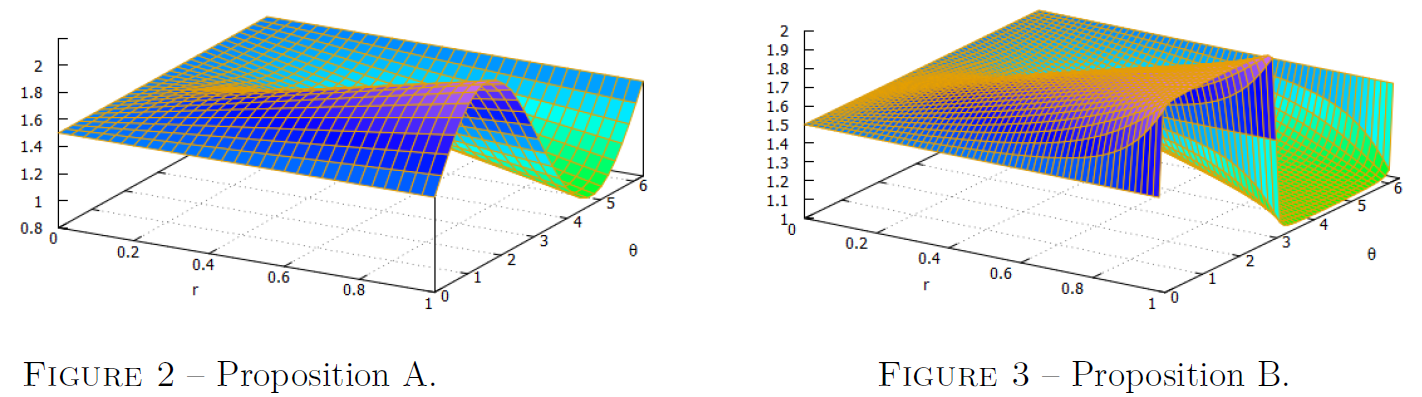
En vous justifiant, laquelle de ces deux figures est celle qui correspond à notre étude ?

Correction
Dans le cas particulier pour lequel T1=2T_1 = 2 et T2=1T_2=1 la propositions de surface de température pour la plaque étudiée qui correspond à notre étude est la Proposition B\textbf{Proposition B} (celle de droite). En effet, c'est la seule qui indique, pour r=1r=1, une discontinuité brutale de température en θ=π\theta = \pi.
Question 21

Démontrer que l'on a :
∑n=0+∞r2n+1sin⁡((2n+1)θ)2n+1=12arctan⁡(2rsin⁡(θ)1−r2)\sum_{n=0}^{+\infty} \dfrac{r^{2n+1} \sin\big( (2n+1) \theta \big)}{2n+1} = \dfrac{1}{2} \arctan\left( \dfrac{2r\sin(\theta)}{1-r^2} \right)

Correction
Notons par :
S=∑p=0+∞(r2p+12p+1sin⁡((2p+1)θ))S = \sum_{p=0}^{+\infty} \left( \dfrac{r^{2p+1}}{2p+1} \sin \big( (2p+1) \theta \big) \right)
On a alors, avec i2=−1i^2 = -1, la relation suivante :
S=∑p=0+∞(r2p+12p+1ei(2p+1)θ−e−i(2p+1)θ2i)S = \sum_{p=0}^{+\infty} \left( \dfrac{r^{2p+1}}{2p+1} \dfrac{ e^{i(2p+1) \theta } - e^{-i(2p+1) \theta } }{2i} \right)
Soit :
S=12i∑p=0+∞(r2p+12p+1(ei(2p+1)θ−e−i(2p+1)θ))S = \dfrac{ 1 }{2i} \sum_{p=0}^{+\infty} \left( \dfrac{r^{2p+1}}{2p+1} \left( e^{i(2p+1) \theta } - e^{-i(2p+1) \theta} \right) \right)
Soit encore :
S=12i∑p=0+∞(r2p+12p+1((eiθ)2p+1−(e−iθ)2p+1))S = \dfrac{ 1 }{2i} \sum_{p=0}^{+\infty} \left( \dfrac{r^{2p+1}}{2p+1} \left( \left( e^{i \theta } \right)^{2p+1} - \left(e^{-i\theta}\right)^{2p+1} \right) \right)
Ce qui s'écrit aussi sous la forme :
S=12i∑p=0+∞(12p+1((reiθ)2p+1−(re−iθ)2p+1))S = \dfrac{ 1 }{2i} \sum_{p=0}^{+\infty} \left( \dfrac{1}{2p+1} \left( \left( re^{i \theta } \right)^{2p+1} - \left( re^{-i\theta}\right)^{2p+1} \right) \right)
En faisant apparaitre les deux sommations, on obtient :
S=12i(∑p=0+∞12p+1(reiθ)2p+1−∑p=0+∞12p+1(re−iθ)2p+1)S = \dfrac{ 1 }{2i} \left( \sum_{p=0}^{+\infty} \dfrac{1}{2p+1} \left( re^{i \theta } \right)^{2p+1} - \sum_{p=0}^{+\infty} \dfrac{1}{2p+1} \left( re^{-i \theta } \right)^{2p+1} \right)
On désigne par zz un nombre complexe de module vérifiant ∣z∣⩽1|z| \leqslant 1. Dans ce cas, on a la série suivante :
argtanh(z)=∑p=0+∞z2p+12p+1\mathrm{argtanh}(z) = \sum_{p=0}^{+\infty} \dfrac{z^{2p+1}}{2p+1}
De fait, on en déduit que :
S=12i(argtanh(reiθ)−argtanh(re−iθ))S = \dfrac{ 1 }{2i} \left( \mathrm{argtanh} \left( re^{i \theta } \right) - \mathrm{argtanh} \left( re^{-i \theta } \right) \right)
De plus, si XX et YY sont deux nombres complexes alors on a :
tanh⁡(X−Y)=tanh⁡(X)−tanh⁡(Y)1−tanh⁡(X)tanh⁡(Y)\tanh(X-Y) = \dfrac{\tanh(X) - \tanh(Y)}{1 - \tanh(X) \tanh(Y)}
Ce qui implique que :
argtanh(tanh⁡(X−Y))=argtanh(tanh⁡(X)−tanh⁡(Y)1−tanh⁡(X)tanh⁡(Y))\mathrm{argtanh} \left( \tanh(X-Y) \right) = \mathrm{argtanh} \left( \dfrac{\tanh(X) - \tanh(Y)}{1 - \tanh(X) \tanh(Y)} \right)
Ce qui nous donne donc :
X−Y=argtanh(tanh⁡(X)−tanh⁡(Y)1−tanh⁡(X)tanh⁡(Y))X-Y = \mathrm{argtanh} \left( \dfrac{\tanh(X) - \tanh(Y)}{1 - \tanh(X) \tanh(Y)} \right)
On pose alors :
{X=argtanh(reiθ)Y=argtanh(re−iθ)\left\lbrace \begin{array}{rcl} X & = & \mathrm{argtanh} \left( re^{i \theta } \right) \\ Y & = & \mathrm{argtanh} \left( re^{-i \theta } \right) \\ \end{array} \right.
Ce qui nous permet d'écrire que :
X−Y=argtanh(tanh⁡(argtanh(reiθ))−tanh⁡(argtanh(re−iθ))1−tanh⁡((argtanh(reiθ))tanh⁡(argtanh(re−iθ)))X-Y = \mathrm{argtanh} \left( \dfrac{\tanh\left( \mathrm{argtanh} \left( re^{i \theta } \right) \right) - \tanh\left( \mathrm{argtanh} \left( re^{-i \theta } \right) \right)}{1 - \tanh(\left( \mathrm{argtanh} \left( re^{i \theta } \right) \right) \tanh\left( \mathrm{argtanh} \left( re^{-i \theta } \right) \right)} \right)
Soit :
X−Y=argtanh(reiθ−re−iθ1−reiθre−iθ)X-Y = \mathrm{argtanh} \left( \dfrac{ re^{i \theta } - re^{-i \theta }}{1 - re^{i \theta } re^{-i \theta } } \right)
Soit encore :
X−Y=argtanh(reiθ−re−iθ1−r2e0)X-Y = \mathrm{argtanh} \left( \dfrac{ re^{i \theta } - re^{-i \theta }}{1 - r^2e^{0}} \right)
En factorisant par rr on obtient :
X−Y=argtanh(r(eiθ−e−iθ)1−r2)X-Y = \mathrm{argtanh} \left( \dfrac{ r \left( e^{i \theta } - e^{-i \theta } \right) }{1 - r^2} \right)
En introduisant la formule d'Euler relative au sinus, on trouve que :
X−Y=argtanh(2ir(eiθ−e−iθ2i)1−r2)=argtanh(2irsin⁡(θ)1−r2)X-Y = \mathrm{argtanh} \left( \dfrac{ 2ir \left( \dfrac{e^{i \theta } - e^{-i \theta }}{2i} \right) }{1 - r^2} \right) = \mathrm{argtanh} \left( \dfrac{ 2ir \sin(\theta) }{1 - r^2} \right)
Ainsi on trouve que :
argtanh(reiθ)−argtanh(re−iθ)=argtanh(i2rsin⁡(θ)1−r2)\mathrm{argtanh} \left( re^{i \theta } \right) - \mathrm{argtanh} \left( re^{-i \theta } \right) = \mathrm{argtanh} \left( i \dfrac{ 2r \sin(\theta) }{1 - r^2} \right)
On désigne par z=ixz=ix un nombre complexe imaginaire pur avec xx un nombre réel tel que ∣x∣⩽1|x| \leqslant 1. Dans ce cas, on a la série suivante :
argtanh(ix)=∑p=0+∞(ix)2p+12p+1=∑p=0+∞i2p+1x2p+12p+1=∑p=0+∞ii2px2p+12p+1=∑p=0+∞i(i2)px2p+12p+1\mathrm{argtanh}(ix) = \sum_{p=0}^{+\infty} \dfrac{(ix)^{2p+1}}{2p+1} = \sum_{p=0}^{+\infty} \dfrac{i^{2p+1}x^{2p+1}}{2p+1} = \sum_{p=0}^{+\infty} \dfrac{ii^{2p}x^{2p+1}}{2p+1} = \sum_{p=0}^{+\infty} \dfrac{i(i^2)^{p}x^{2p+1}}{2p+1}
Donc :
argtanh(ix)=∑p=0+∞i(−1)px2p+12p+1\mathrm{argtanh}(ix) = \sum_{p=0}^{+\infty} \dfrac{i(-1)^{p}x^{2p+1}}{2p+1}
Ou encore :
argtanh(ix)=i∑p=0+∞(−1)px2p+12p+1\mathrm{argtanh}(ix) = i \sum_{p=0}^{+\infty} \dfrac{(-1)^{p}x^{2p+1}}{2p+1}
Or, pour xx réel appartenant à l'intervalle [−1 ; 1][-1 \,;\, 1] on a la somme suivante :
∑p=0+∞(−1)px2p+12p+1=arctan⁡(x)\sum_{p=0}^{+\infty} \dfrac{(-1)^{p}x^{2p+1}}{2p+1} = \arctan(x)
Ainsi, on en déduit que :
argtanh(ix)=iarctan⁡(x)\mathrm{argtanh}(ix) = i \arctan(x)
Ce qui nous permet d'écrire que :
argtanh(reiθ)−argtanh(re−iθ)=iarctan⁡(2rsin⁡(θ)1−r2)\mathrm{argtanh} \left( re^{i \theta } \right) - \mathrm{argtanh} \left( re^{-i \theta } \right) = i \arctan\left( \dfrac{ 2r \sin(\theta) }{1 - r^2} \right)
Donc :
argtanh(reiθ)−argtanh(re−iθ)i=arctan⁡(2rsin⁡(θ)1−r2)\dfrac{\mathrm{argtanh} \left( re^{i \theta } \right) - \mathrm{argtanh} \left( re^{-i \theta } \right)}{i} = \arctan\left( \dfrac{ 2r \sin(\theta) }{1 - r^2} \right)
Soit encore :
12i(argtanh(reiθ)−argtanh(re−iθ))=12arctan⁡(2rsin⁡(θ)1−r2)\dfrac{ 1 }{2i} \left( \mathrm{argtanh} \left( re^{i \theta } \right) - \mathrm{argtanh} \left( re^{-i \theta } \right) \right) = \dfrac{1}{2}\arctan\left( \dfrac{ 2r \sin(\theta) }{1 - r^2} \right)
On écrit alors que :
S=12arctan⁡(2rsin⁡(θ)1−r2)S = \dfrac{1}{2}\arctan\left( \dfrac{ 2r \sin(\theta) }{1 - r^2} \right)
Finalement, on peut donc en conclure que :
∑p=0+∞(r2p+12p+1sin⁡((2p+1)θ))=12arctan⁡(2rsin⁡(θ)1−r2){\color{red}{\boxed{ \sum_{p=0}^{+\infty} \left( \dfrac{r^{2p+1}}{2p+1} \sin \big( (2p+1) \theta \big) \right) = \dfrac{1}{2}\arctan\left( \dfrac{ 2r \sin(\theta) }{1 - r^2} \right) }}}
Ceci explique la formule donnée en complément du sujet proposée.

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.