Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 14 - Exercice 1
2 h
165
Un exercice ou une démarche scientifique transversale est indispensable. Vous meilleurs atouts seront les initiatives, la rigueur, la patiences, accepter de se tromper et de recommencer.
Question 1
Soit .
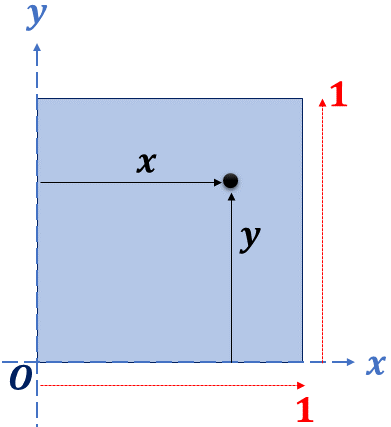
Un tambour est constitué d'une membrane horizontale tendue et carrée de côté unité. Son bord est représenté par un carré .
On supposera que cette membrane est à chaque instant élastique, homogène et isotrope. Nous supposerons également que les déplacement verticaux engendrés font que cette membrane reste dans des états physiques qui conservent sont élasticité linéaire, son homogénéité et son isotropie. Cela induit, à chaque instant, des de cette membrane.
On suppose qu'à l'instant initial on déplace verticalement la membrane. On note par et , avec , les coordonnées des points matériels (physiques) de cette membrane.
On adopte la géométrie naturelle suivante :
L'amplitude de la déformation verticale initiale de cette membrane se modélise par l'expression .
La fonction est dérivable au moins deux fois sur le domaine que défini la membrane. En outre, et sa dérivée première, selon et , sont bornées sur ce même domaine.
Puis, on instantanément l'action mécanique à l'origine de cette déformation verticale. Typiquement, il peut s'agir d'une frappe de la paume d'une main humaine.
On notera par la déformation verticale, par rapport au plan horizontal d'équilibre, se produisant au point de coordonnées à l'instant .
Bien évidemment la déformation verticale est bornée (afin de s'assurer que la membrane ne soit pas détruite) de telle façon à pouvoir écrire que :
Le fait de relâcher la membrane juste après la déformation initiale, d'amplitude , implique que la vitesse verticale de la membrane est nulle à l'instant initial. Ceci implique la condition :
Et on a également la condition initiale suivante :
Le fait d'avoir une membrane qui soit homogène et isotrope, caractéristiques auxquelles on adjoint la condition d'existence physique de la membrane, nous permet d'envisager une vitesse de propagation longitudinale que nous noterons .
Le fait que le bord de la membrane soit fixe (donc mécaniquement solidaire du socle rigide du tambour) implique les conditions mathématiques, dites de bord, suivante :
L'équation, aux dérivées partielles (EDP), qui gouverne les évolutions spatiales et temporelles des déformations verticales est :
Soit encore :
Les conditions et hypothèses, fixant le cadre de ce travail, permettent d'envisager l'écriture d'une solution, mathématiquement et physiquement acceptable, de la forme (dénommée " ") suivante :
Les termes , et désignent trois fonctions réelles continues sur les intervalles considérés.
Un tambour est constitué d'une membrane horizontale tendue et carrée de côté unité. Son bord est représenté par un carré .
On supposera que cette membrane est à chaque instant élastique, homogène et isotrope. Nous supposerons également que les déplacement verticaux engendrés font que cette membrane reste dans des états physiques qui conservent sont élasticité linéaire, son homogénéité et son isotropie. Cela induit, à chaque instant, des de cette membrane.
On suppose qu'à l'instant initial on déplace verticalement la membrane. On note par et , avec , les coordonnées des points matériels (physiques) de cette membrane.
On adopte la géométrie naturelle suivante :

L'amplitude de la déformation verticale initiale de cette membrane se modélise par l'expression .
La fonction est dérivable au moins deux fois sur le domaine que défini la membrane. En outre, et sa dérivée première, selon et , sont bornées sur ce même domaine.
Puis, on instantanément l'action mécanique à l'origine de cette déformation verticale. Typiquement, il peut s'agir d'une frappe de la paume d'une main humaine.
On notera par la déformation verticale, par rapport au plan horizontal d'équilibre, se produisant au point de coordonnées à l'instant .
Bien évidemment la déformation verticale est bornée (afin de s'assurer que la membrane ne soit pas détruite) de telle façon à pouvoir écrire que :
Le fait de relâcher la membrane juste après la déformation initiale, d'amplitude , implique que la vitesse verticale de la membrane est nulle à l'instant initial. Ceci implique la condition :
Et on a également la condition initiale suivante :
Le fait d'avoir une membrane qui soit homogène et isotrope, caractéristiques auxquelles on adjoint la condition d'existence physique de la membrane, nous permet d'envisager une vitesse de propagation longitudinale que nous noterons .
Le fait que le bord de la membrane soit fixe (donc mécaniquement solidaire du socle rigide du tambour) implique les conditions mathématiques, dites de bord, suivante :
L'équation, aux dérivées partielles (EDP), qui gouverne les évolutions spatiales et temporelles des déformations verticales est :
Soit encore :
Les conditions et hypothèses, fixant le cadre de ce travail, permettent d'envisager l'écriture d'une solution, mathématiquement et physiquement acceptable, de la forme (dénommée " ") suivante :
Les termes , et désignent trois fonctions réelles continues sur les intervalles considérés.
Déterminer l'expression générale des déformations verticales .
Correction
Posons :
Ainsi :
Soit :
Donc :
Ainsi :
On a aussi :
Donc :
Ainsi :
On a également :
Donc :
Ainsi :
L'équation gouvernant les vibrations de la membrane devient :
Comme ne peut être nulle partout et tout le temps, on peut simplifier par cette quantité, globalement non nulle. Donc :
Enfin, on obtient :
Le terme de gauche à une variabilité temporelle alors que celui de droite une variabilité positionnelle. C'est pourquoi l'égalité que traduit cette équation ne peut être satisfaite que si chacun de ses membres de gauche et droit soit égal à une même constante réelle . On a alors :
Soit encore :
Le terme est une quantité réelle et la présence du carré de nous suggère d'écrire sous la forme avec qui est un nombre réel positif, et de fait . Donc :
Si alors et on a :
Donc, pour , on a :
Cependant, lorsque les deux termes et se comportent (asymptotiquement) comme et fait divergent car et . La divergence implique que la condition :
n'est pas satisfaite. Donc cette première situation n'est physiquement pas possible.
Si alors et on a :
Donc, pour , on a :
Lorsque le terme diverge. Cette divergence implique que la condition , à savoir
n'est pas satisfaite. Donc on en déduit que et nous obtenons . Ainsi, on trouve que :
Dès lors les déplacements sont stationnaires. Ce qui signifie que la membrane du tambour ne bouge plus et qu'il n'y a plus de déplacement vertical dans le temps. Donc cette deuxième situation n'est physiquement pas possible.
Si alors et on a :} }
Donc, pour , on a :
Exploitons maintenant la condition . On a :
Donc :
Ainsi :
On a alors :
Comme n'est pas nulle (sinon cela signifie qu'il n'y a pas de déformation initialement) cela implique que et . Donc :
Ainsi :
Comme alors la condition impose . Et de fait :
Et on a ce qui implique que .
On a donc :
Soit :
Le terme de gauche à une variabilité horizontale alors que celui de droite une variabilité verticale. C'est pourquoi l'égalité que traduit cette équation ne peut être satisfaite que si chacun de ses membres de gauche et droit soit égal à une même constante réelle . On a alors :
Soit :
Ce qui précède nous suggère d'écrire sous la forme avec qui est un nombre réel positif, et de fait . Donc :
Si alors et on a :
Donc, pour , on a :
Par hypothèse, la dépendance horizontale doit être bornée. Ceci n'est pas possible avec les fonctions hyperboliques. Donc cette première situation n'est physiquement pas possible.
Si alors et on a :
Donc, pour , on a :
Par hypothèse, la dépendance horizontale doit être bornée. Ceci n'est pas possible avec une fonction affine. Donc cette deuxième situation n'est physiquement pas possible.
Si alors et on a :
Donc, pour , on a :
Par hypothèse, la dépendance horizontale doit être bornée. Ceci est possible avec les fonctions trigonométriques classiques. Ainsi on conserve la situation correspondante à .
Ceci nous donne donc :
Donc :
Soit encore :
D'où :
Les solutions verticales recherchées sont bien connues. Les formes qui seront physiquement acceptables imposent, d'après ce qui précède, que . On a donc la forme analytique suivante :
On en déduit donc que :
Mais, par hypothèse, on sait que . Donc :
Soit :
Donc on en déduit que . Ainsi :
Mais, par hypothèse, on sait que . Donc :
Soit :
Soit encore :
Ceci impose d'avoir . Ce qui nous permet d'écrire que :
En regroupant les constantes réelles, on obtient :
Puis, on a la condition . Donc :
Ce qui implique que :
Puis, on a la condition . Donc :
Ce qui implique également que :
Ainsi, on en déduit que :
Soit (comme cosinus est pair, le signe n'est pas important) :
Ainsi, on obtient l'expression physique et mathématique des déformations transversales de la membrane suivante :
Le fait d'avoir une élasticité linéaire implique que que toutes combinaisons linéaires de termes de la forme précédente, solution de l'équation étudiée sous les hypothèses qui cadrent cette étude, est également une solution mathématique qui est physiquement acceptable. Donc, en sommant sur toutes les valeurs possibles des entiers et , on trouve que :
Avec .
Puis, la condition
nous donne, donc avec et , la relation suivante :
Soit :
Posons alors :
D'où :
Il apparaît alors clairement un développement en série de Fourier sur une période de . De fait, on a immédiatement l'expression du coefficient
Cette dernière relation montre que est une fonction -périodique de la variable . Donc, la relation est un développement en série de Fourier dont les coefficients sont donnés par l'expression suivante :
De fait, on en déduit que :
Soit :
Finalement, la solution théorique globale est donnée par la formule suivante :
Les fréquences de vibrations de la membrane du tambour vont être déterminées par le terme en dépendance temporelle, à savoir .
Si on note par les pulsations associées à ces vibrations, on a alors :
Donc :
Ce qui nous donne :
Ainsi, les fréquences de vibrations de la membrane du tambour sont données par l'expression :
Si on désigne par la tension linéique de la membrane et par la masse surfacique de cette même membrane, alors Avec la vitesse longitudinale est donnée par la formule :
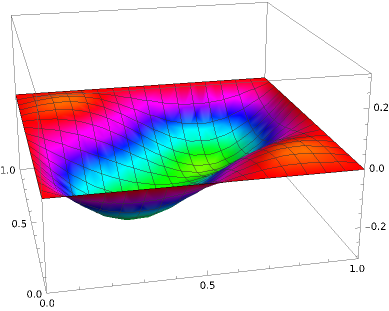
D'un point de vue graphique, voici la représentation tridimensionnelle de la vibration et à un instant fixé de la membrane carrée de ce tambour :
Ainsi :
Soit :
Donc :
Ainsi :
On a aussi :
Donc :
Ainsi :
On a également :
Donc :
Ainsi :
L'équation gouvernant les vibrations de la membrane devient :
Comme ne peut être nulle partout et tout le temps, on peut simplifier par cette quantité, globalement non nulle. Donc :
Enfin, on obtient :
Le terme de gauche à une variabilité temporelle alors que celui de droite une variabilité positionnelle. C'est pourquoi l'égalité que traduit cette équation ne peut être satisfaite que si chacun de ses membres de gauche et droit soit égal à une même constante réelle . On a alors :
Soit encore :
Le terme est une quantité réelle et la présence du carré de nous suggère d'écrire sous la forme avec qui est un nombre réel positif, et de fait . Donc :
Si alors et on a :
Donc, pour , on a :
Cependant, lorsque les deux termes et se comportent (asymptotiquement) comme et fait divergent car et . La divergence implique que la condition :
n'est pas satisfaite. Donc cette première situation n'est physiquement pas possible.
Si alors et on a :
Donc, pour , on a :
Lorsque le terme diverge. Cette divergence implique que la condition , à savoir
n'est pas satisfaite. Donc on en déduit que et nous obtenons . Ainsi, on trouve que :
Dès lors les déplacements sont stationnaires. Ce qui signifie que la membrane du tambour ne bouge plus et qu'il n'y a plus de déplacement vertical dans le temps. Donc cette deuxième situation n'est physiquement pas possible.
Si alors et on a :} }
Donc, pour , on a :
Exploitons maintenant la condition . On a :
Donc :
Ainsi :
On a alors :
Comme n'est pas nulle (sinon cela signifie qu'il n'y a pas de déformation initialement) cela implique que et . Donc :
Ainsi :
Comme alors la condition impose . Et de fait :
Et on a ce qui implique que .
On a donc :
Soit :
Le terme de gauche à une variabilité horizontale alors que celui de droite une variabilité verticale. C'est pourquoi l'égalité que traduit cette équation ne peut être satisfaite que si chacun de ses membres de gauche et droit soit égal à une même constante réelle . On a alors :
Soit :
Ce qui précède nous suggère d'écrire sous la forme avec qui est un nombre réel positif, et de fait . Donc :
Si alors et on a :
Donc, pour , on a :
Par hypothèse, la dépendance horizontale doit être bornée. Ceci n'est pas possible avec les fonctions hyperboliques. Donc cette première situation n'est physiquement pas possible.
Si alors et on a :
Donc, pour , on a :
Par hypothèse, la dépendance horizontale doit être bornée. Ceci n'est pas possible avec une fonction affine. Donc cette deuxième situation n'est physiquement pas possible.
Si alors et on a :
Donc, pour , on a :
Par hypothèse, la dépendance horizontale doit être bornée. Ceci est possible avec les fonctions trigonométriques classiques. Ainsi on conserve la situation correspondante à .
Ceci nous donne donc :
Donc :
Soit encore :
D'où :
Les solutions verticales recherchées sont bien connues. Les formes qui seront physiquement acceptables imposent, d'après ce qui précède, que . On a donc la forme analytique suivante :
On en déduit donc que :
Mais, par hypothèse, on sait que . Donc :
Soit :
Donc on en déduit que . Ainsi :
Mais, par hypothèse, on sait que . Donc :
Soit :
Soit encore :
Ceci impose d'avoir . Ce qui nous permet d'écrire que :
En regroupant les constantes réelles, on obtient :
Puis, on a la condition . Donc :
Ce qui implique que :
Puis, on a la condition . Donc :
Ce qui implique également que :
Ainsi, on en déduit que :
Soit (comme cosinus est pair, le signe n'est pas important) :
Ainsi, on obtient l'expression physique et mathématique des déformations transversales de la membrane suivante :
Le fait d'avoir une élasticité linéaire implique que que toutes combinaisons linéaires de termes de la forme précédente, solution de l'équation étudiée sous les hypothèses qui cadrent cette étude, est également une solution mathématique qui est physiquement acceptable. Donc, en sommant sur toutes les valeurs possibles des entiers et , on trouve que :
Avec .
Puis, la condition
nous donne, donc avec et , la relation suivante :
Soit :
Posons alors :
D'où :
Il apparaît alors clairement un développement en série de Fourier sur une période de . De fait, on a immédiatement l'expression du coefficient
Cette dernière relation montre que est une fonction -périodique de la variable . Donc, la relation est un développement en série de Fourier dont les coefficients sont donnés par l'expression suivante :
De fait, on en déduit que :
Soit :
Finalement, la solution théorique globale est donnée par la formule suivante :
Les fréquences de vibrations de la membrane du tambour vont être déterminées par le terme en dépendance temporelle, à savoir .
Si on note par les pulsations associées à ces vibrations, on a alors :
Donc :
Ce qui nous donne :
Ainsi, les fréquences de vibrations de la membrane du tambour sont données par l'expression :
Si on désigne par la tension linéique de la membrane et par la masse surfacique de cette même membrane, alors Avec la vitesse longitudinale est donnée par la formule :
D'un point de vue graphique, voici la représentation tridimensionnelle de la vibration et à un instant fixé de la membrane carrée de ce tambour :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.