Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Tchat avec un prof

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Exercice 13 - Exercice 1

1 h
85
On considère une fonction numérique réelle ff, telle que f:t∈R⟶f(t)∈Rf : t \in \mathbb{R} \longrightarrow f(t) \in \mathbb{R}, au moins de classe C1\mathcal{C}^1 sur R\mathbb{R}.
De plus, on suppose que cette fonction réelle ff est TT-périodique, avec TT qui est un nombre réel strictement positif.
Soit α\alpha un nombre réel strictement positif. On considère alors l'équation différentielle (E)(\mathcal{E}) suivante :
(E):    x′(t)+α x(t)=f(t)(\mathcal{E}) :\,\,\,\, x'(t) + \alpha \, x(t) = f(t)
La fonction numérique réelle xx qui est solution de (E)(\mathcal{E}) est également supposée de classe C1\mathcal{C}^1 sur R\mathbb{R}, et également TT-périodique.
Cette TT-périodicité de ff et xx nous invite à les exprimer selon un développement en série de Fourier\textit{Fourier}, selon :
{f(t)=a02+∑n=1+∞(ancos⁡(nωt)+bnsin⁡(nωt))x(t)=A02+∑n=1+∞(Ancos⁡(nωt)+Bnsin⁡(nωt))      avec :  ω=2πT  et  n∈N⋆\left\lbrace \begin{array}{rcl} f(t) & = & \dfrac{a_0}{2} + \displaystyle{\sum_{n = 1}^{+ \infty}} \left( a_n \cos(n \omega t) + b_n \sin(n \omega t)\right) \\ & & \\ x(t) & = & \dfrac{A_0}{2} + \displaystyle{\sum_{n = 1}^{+ \infty}} \left( A_n \cos(n \omega t) + B_n \sin(n \omega t)\right) \\ \end{array} \right. \,\,\,\,\,\, \mathrm{avec} \, : \,\, \omega = \dfrac{2\pi}{T} \,\, \mathrm{et} \,\, n \in \mathbb{N}^\star
Tous les coefficients ana_n, bnb_n, AnA_n et BnB_n, qui apparaissent dans les développements en série de Fourier\textit{Fourier} de ff et xx, sont des grandeurs réelles.
Le but de cette meˊthode de reˊsolution {\color{red}{\textbf{Le but de cette méthode de résolution }}} est de trouver l'expression des coefficients de Fourier\textit{Fourier} A0A_0, AnA_n et BnB_n de x(t)x(t) en fonction de a0a_0, ana_n et ana_n, ceux de f(t)f(t).
Question 1
Partie 1 : Geˊneˊraliteˊs\textbf{{\color{MidnightBlue}{\textsf{Partie 1 : Généralités}}}}

Déterminer l'expression de x′(t)x'(t) uniquement en fonction des coefficients de Fourier\textit{Fourier} A0A_0, AnA_n et BnB_n.

Correction
L'expression de x′(t)x'(t) est donnée par :
x′(t)=∑n=1+∞(nωBncos⁡(nωt)−nωAnsin⁡(nωt))x'(t) = \sum_{n = 1}^{+ \infty} \left( n \omega B_n \cos(n \omega t) - n \omega A_n \sin(n \omega t)\right)
Question 2

Déterminer l'expression de x′(t)+α x(t)x'(t) + \alpha \, x(t) uniquement en fonction des coefficients de Fourier\textit{Fourier} A0A_0, AnA_n et BnB_n.

Correction
L'expression de x′(t)+α x(t)x'(t) + \alpha \, x(t) est :
x′(t)+α x(t)=αA02+∑n=1+∞((nωBn+αAn)cos⁡(nωt)+(αBn−nωAn)sin⁡(nωt))x'(t) + \alpha \, x(t) = \dfrac{\alpha A_0}{2} + \sum_{n = 1}^{+ \infty} \left( \left(n \omega B_n + \alpha A_n \right) \cos(n \omega t) + \left( \alpha B_n - n \omega A_n \right) \sin(n \omega t)\right)
Question 3

En déduire l'expression de A0A_0, AnA_n et BnB_n en fonction de a0a_0, ana_n, bnb_n, α\alpha, nn et TT.

Correction
On a l'égalité suivante :
x′(t)+α x(t)=f(t)x'(t) + \alpha \, x(t) = f(t)
Ce qui nous donne donc :
αA02+∑n=1+∞((nωBn+αAn)cos⁡(nωt)+(αBn−nωAn)sin⁡(nωt))=a02+∑n=1+∞(ancos⁡(nωt)+bnsin⁡(nωt))\dfrac{\alpha A_0}{2} + \displaystyle{\sum_{n = 1}^{+ \infty}} \left( \left(n \omega B_n + \alpha A_n \right) \cos(n \omega t) + \left( \alpha B_n - n \omega A_n \right) \sin(n \omega t)\right) = \dfrac{a_0}{2} + \displaystyle{\sum_{n = 1}^{+ \infty}} \left( a_n \cos(n \omega t) + b_n \sin(n \omega t)\right)
Ce qui nous permet les identifications suivantes :
{αA0=a0nωBn+αAn=anαBn−nωAn=bn\left\lbrace \begin{array}{rcl} \alpha A_0 & = & a_0 \\ & & \\ n \omega B_n + \alpha A_n & = & a_n \\ & & \\ \alpha B_n - n \omega A_n & = & b_n \\ \end{array} \right.
Ce qui nous donne :
{A0=a0αAn=αan−nωbn(nω)2+α2Bn=αbn+nωan(nω)2+α2\left\lbrace \begin{array}{rcl} A_0 & = & \dfrac{a_0}{\alpha} \\ & & \\ A_n & = & \dfrac{\alpha a_n - n \omega b_n}{(n\omega)^2 + \alpha^2} \\ & & \\ B_n & = & \dfrac{\alpha b_n + n \omega a_n}{(n\omega)^2 + \alpha^2} \\ \end{array} \right.
Question 4
Partie 2 : Application\textbf{{\color{MidnightBlue}{\textsf{Partie 2 : Application}}}}
On choisit les valeurs numériques suivantes :
∙  \bullet \,\ α=1\alpha = 1 ;
∙  \bullet \,\ T=2πT = 2 \pi.
La fonction ff, qui est 2π2\pi-périodique, est maintenant définit par :
f(t)={(t−π2)2si0⩽t⩽π−(t−3π2)2+π22siπ⩽t⩽2πf(t) = \left\lbrace \begin{array}{rcccccc} \left( t - \dfrac{\pi}{2} \right)^2 & \mathrm{si} & 0 & \leqslant & t & \leqslant \pi \\ & & & & & \\ - \left( t - \dfrac{3\pi}{2} \right)^2 + \dfrac{\pi^2}{2}& \mathrm{si} & \pi & \leqslant & t & \leqslant 2\pi \\ \end{array} \right.
La représentation graphique de ff est :

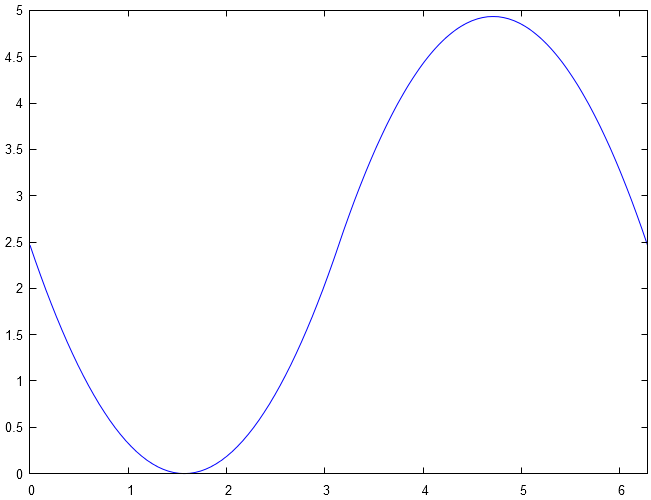
Déterminer le coefficient de Fourier\textit{Fourier} a0a_0 associé à ff.

Correction
On choisit les valeurs numériques suivantes :
∙  \bullet \,\, α=1\alpha = 1 ;
∙  \bullet \,\, T=2πT = 2 \pi.
On a alors ω=1\omega = 1, et donc les expressions suivantes :
{A0=a0An=an−nbnn2+1Bn=bn+nann2+1\left\lbrace \begin{array}{rcl} A_0 & = & a_0 \\ & & \\ A_n & = & \dfrac{a_n - n b_n}{n^2 + 1} \\ & & \\ B_n & = & \dfrac{b_n + n a_n}{n^2 + 1} \\ \end{array} \right.
Le coefficient de Fourier\textit{Fourier} a0a_0 associé à ff est donné par :
a0=1π[∫0π(t−π2)2 dt+∫π2π(−(t−3π2)2+π22) dt]=π22a_0 = \dfrac{1}{\pi} \left[ \int_0^\pi \left( t - \dfrac{\pi}{2} \right)^2 \, dt + \int_\pi^{2\pi} \left( - \left( t - \dfrac{3\pi}{2} \right)^2 + \dfrac{\pi^2}{2} \right) \, dt \right] = \dfrac{\pi^2}{2}
Ce qui fait une valeur moyenne à π24≃2,5\dfrac{\pi^2}{4} \simeq 2,5 ce qui est bien la valeur observée sur la graphique proposé dans le sujet.
Question 5

Déterminer le coefficient de Fourier\textit{Fourier} ana_n (an∈N⋆a_n \in \mathbb{N}^\star) associé à ff.

Correction
Le coefficient de Fourier\textit{Fourier} ana_n est :
an=1π[∫0π(t−π2)2cos⁡(nt) dt+∫π2π(−(t−3π2)2+π22)cos⁡(nt)  dt]=0a_n = \dfrac{1}{\pi} \left[ \int_0^\pi \left( t - \dfrac{\pi}{2} \right)^2 \cos(nt) \, dt + \int_\pi^{2\pi} \left( - \left( t - \dfrac{3\pi}{2} \right)^2 + \dfrac{\pi^2}{2} \right) \cos(nt) \, \, dt \right] = 0
Question 6

Déterminer le coefficient de Fourier\textit{Fourier} bnb_n (bn∈N⋆b_n \in \mathbb{N}^\star) associé à ff.

Correction
Le coefficient de \textit{Fourier} bnb_n est :
bn=1π[∫0π(t−π2)2sin⁡(nt) dt+∫π2π(−(t−3π2)2+π22)sin⁡(nt)  dt]=4((−1)n−1)πn3b_n = \dfrac{1}{\pi} \left[ \int_0^\pi \left( t - \dfrac{\pi}{2} \right)^2 \sin(nt) \, dt + \int_\pi^{2\pi} \left( - \left( t - \dfrac{3\pi}{2} \right)^2 + \dfrac{\pi^2}{2} \right) \sin(nt) \, \, dt \right] = \dfrac{4 \left( (-1)^n - 1 \right)}{\pi n^3}
La présence du terme (−1)n(-1)^n nous invite à distinguer la parité de nn. On a alors :
  ∙  \,\, \bullet \,\, si nn est pair alors n=2kn=2k (k∈N)(k \in \mathbb{N}) :
dans ce cas (−1)n=(−1)2k=((−1)2)k=1k=1(-1)^{n} = (-1)^{2k} = \left((-1)^2\right)^k = 1^k = 1.
Et on en déduit que :
b2k=0b_{2k} = 0
  ∙  \,\, \bullet \,\, si nn est impair alors n=2k+1n=2k+1 (k∈N)(k \in \mathbb{N}) :
dans ce cas (−1)n=(−1)2k+1=((−1)2)k×(−1)=−1(-1)^{n} = (-1)^{2k+1} = \left((-1)^2\right)^k \times (-1) = -1.
Et on en déduit que :
b2k+1=4(−1−1)π(2k+1)3=−8π(2k+1)3b_{2k+1} = \dfrac{4 \left( -1 - 1 \right)}{\pi (2k+1)^3} = -\dfrac{8}{\pi (2k+1)^3}
Question 7

En déduire l'expression des coefficients de Fourier\textit{Fourier} de x(t)x(t).

Correction
On en déduit que :
{A0=π22A2k=0−n0n2+1=0B2k=0+n0n2+1=0A2k+1=0−(2k+1)×−(8π(2k+1)3)(2k+1)2+1=8π(2k+1)2((2k+1)2+1)B2k+1=−8π(2k+1)3+n0(2k+1)2+1=−8π(2k+1)3((2k+1)2+1)\left\lbrace \begin{array}{rcl} A_0 & = & \dfrac{\pi^2}{2} \\ & & \\ A_{2k} & = & \dfrac{0 - n 0}{n^2 + 1} = 0 \\ & & \\ B_{2k} & = & \dfrac{0 + n 0}{n^2 + 1} = 0 \\ & & \\ A_{2k+1} & = & \dfrac{0 - (2k+1) \times - \left(\dfrac{8}{\pi (2k+1)^3} \right) }{(2k+1)^2 + 1} = \dfrac{8}{\pi (2k+1)^2 \left( (2k+1)^2 + 1 \right) } \\ & & \\ B_{2k+1} & = & \dfrac{-\dfrac{8}{\pi (2k+1)^3} + n 0}{(2k+1)^2 + 1} = - \dfrac{8}{\pi (2k+1)^3 \left( (2k+1)^2 + 1 \right) } \\ \end{array} \right.
Question 8

Déterminer l'expression du développement en série de Fourier\textit{Fourier} de x(t)x(t).

Correction
L'expression du développement en série de Fourier\textit{Fourier} de x(t)x(t) est :
x(t)=π24+8π∑k=0+∞(cos⁡((2k+1)t)(2k+1)2((2k+1)2+1)−sin⁡((2k+1)t)(2k+1)3((2k+1)2+1))x(t) = \dfrac{\pi^2}{4} + \dfrac{8}{\pi}\displaystyle{\sum_{k = 0}^{+ \infty}} \left( \dfrac{\cos((2k+1) t)}{(2k+1)^2 \left( (2k+1)^2 + 1 \right)} - \dfrac{\sin((2k+1)t)}{(2k+1)^3 \left( (2k+1)^2 + 1 \right)} \right)

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.