Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 12 - Exercice 1
1 h 30 min
120
Un exercice pour traiter les signaux les plus usuels en traitement du signal.
Question 1
Soit un nombre réel strictement positif. Soit un nombre réel strictement positif. Soit une fonction numérique -périodique, telle que :
Représenter graphiquement la fonction .
Correction
On a la représentation graphique suivante :
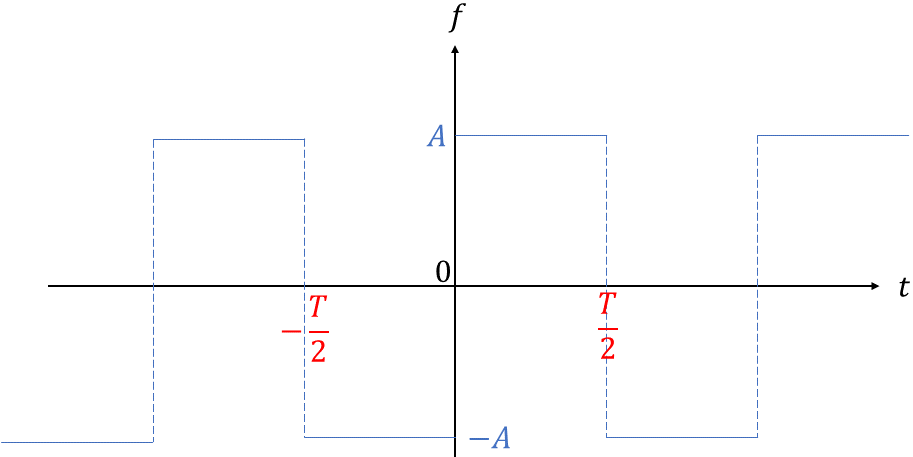

Question 2
Déterminer la série de associée.
Correction
La fonction étant impaire, on en déduit que :
Puis :
Soit :
D'où :
Ainsi :
En intégrant :
D'où :
On obtient alors :
La fonction cosinus étant paire, on en déduit que :
Ce qui nous permet d'écrire que :
Donc :
Or, on sait que . D'où :
De plus, on a :
Ainsi :
On constate que pour tout les pairs, on a . Donc, seul les termes de impairs sont non-nuls. Soit , et on pose . Ce qui nous permet d'écrire que :
On obtient alors :
Finalement :
Et on trouve alors que :
Puis :
Soit :
D'où :
Ainsi :
En intégrant :
D'où :
On obtient alors :
La fonction cosinus étant paire, on en déduit que :
Ce qui nous permet d'écrire que :
Donc :
Or, on sait que . D'où :
De plus, on a :
Ainsi :
On constate que pour tout les pairs, on a . Donc, seul les termes de impairs sont non-nuls. Soit , et on pose . Ce qui nous permet d'écrire que :
On obtient alors :
Finalement :
Et on trouve alors que :
Question 3
Justifier que la série la série de converge bien vers .$
Correction
La fonction . Donc la série converge vers .
Question 4
Déterminer la valeur de la série numérique suivante :
Correction
Plaçons nous à l'instant particulier . On a alors :
Ce qui nous donne :
Soit :
Soit encore :
Or, on a . Donc, on en déduit que :
Finalement, la valeur de la série numérique est la suivante :
Ce qui nous donne :
Soit :
Soit encore :
Or, on a . Donc, on en déduit que :
Finalement, la valeur de la série numérique est la suivante :
Question 5
Soit un nombre réel strictement positif. Soit un nombre réel strictement positif. Soit une fonction numérique -périodique, telle que :
Représenter graphiquement la fonction .
Correction
On a la représentation graphique suivante :
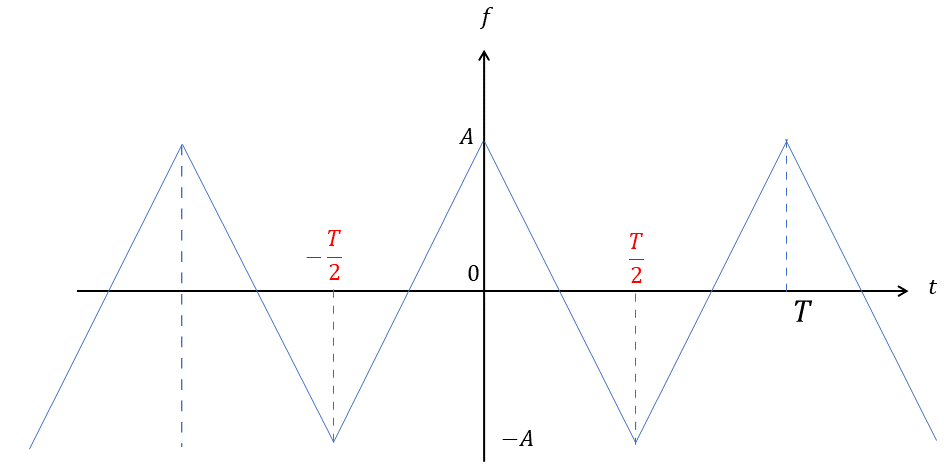

Question 6
Déterminer la série de associée.
Correction
La fonction étant paire, on en déduit que :
Puis, on a :
Comme est paire, on en déduit que :
Soit :
Donc :
On a alors :
Ainsi, on trouve que :
Puis, pour , on a :
Puis, comme est paire, ainsi que la fonction cosinus, on en déduit que :
Donc :
Ainsi :
Avec :
Et :
Puis :
Donc :
On peut donc alors écrire que :
Or, . Donc :
On constate que si est pair alors . Ainsi, posons , avec . On en déduit alors que :
Ce qui nous donne :
Et on trouve alors que :
Puis, on a :
Comme est paire, on en déduit que :
Soit :
Donc :
On a alors :
Ainsi, on trouve que :
Puis, pour , on a :
Puis, comme est paire, ainsi que la fonction cosinus, on en déduit que :
Donc :
Ainsi :
Avec :
Et :
Puis :
Donc :
On peut donc alors écrire que :
Or, . Donc :
On constate que si est pair alors . Ainsi, posons , avec . On en déduit alors que :
Ce qui nous donne :
Et on trouve alors que :
Question 7
Justifier que la série la série de converge bien vers .
Correction
La fonction . Donc la série converge vers .
Question 8
Déterminer la valeur de la série numérique suivante :
Correction
Plaçons nous dans le cas ou . Dans ce cas, la Série de Fourier est égale à :
Donc :
Soit :
Comme , on en déduit que :
En simplifiant par , on obtient :
Finalement, on en déduit que :
Donc :
Soit :
Comme , on en déduit que :
En simplifiant par , on obtient :
Finalement, on en déduit que :
Question 9
Soit un nombre réel strictement positif, appelée largeur impulsionnelle.
Soit un nombre réel strictement positif. Soit un nombre réel strictement positif. On suppose que . Soit une fonction numérique -périodique, telle que :
Représenter graphiquement la fonction .
Correction
On a la représentation graphique suivante :
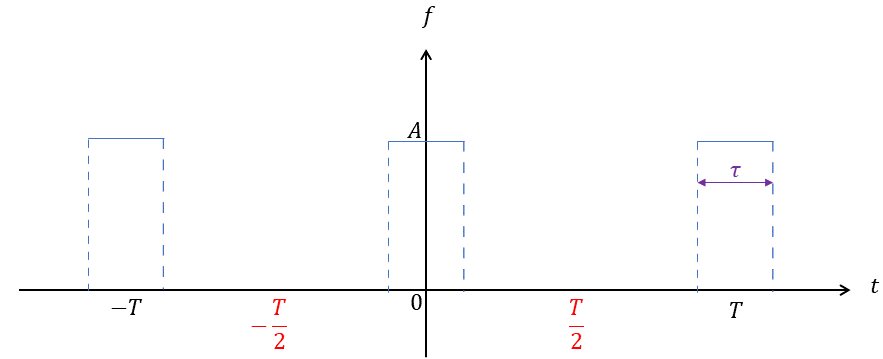

Question 10
Déterminer la série de associée.
Correction
La fonction étant paire, on en déduit que :
Puis, on a :
Comme est paire, on en déduit que :
Soit :
Donc :
Puis, pour , on a :
Puis, comme est paire, ainsi que la fonction cosinus, on en déduit que :
Donc :
Ainsi :
Cependant, on a , ce qui nous permet d'avoir . Donc, on obtient :
Soit encore :
Ce qui nous permet d'écrire que :
Soit :
Finalement :
Puis, on a :
Comme est paire, on en déduit que :
Soit :
Donc :
Puis, pour , on a :
Puis, comme est paire, ainsi que la fonction cosinus, on en déduit que :
Donc :
Ainsi :
Cependant, on a , ce qui nous permet d'avoir . Donc, on obtient :
Soit encore :
Ce qui nous permet d'écrire que :
Soit :
Finalement :
Question 11
Justifier que la série la série de converge bien vers .
Correction
La fonction . Donc la série converge vers .
Question 12
Étudier la situation lors que la largeur impulsionnelle tend vers .
Correction
On a :
Soit encore :
Or, on sait que :
Donc, si on pose , on constate que lorsque alors . De fait :
Soit :
Soit encore :
Donc :
La subtilité est dans la somme . En effet, lorsque , cette somme diverge. Afin d'expliquer cela, posons , et on a :
Donc à , on a :
Le terme peut donner un nombre fini non nul lorsque . Lorsque , la fonction est oscillante mais de très faible amplitude. A titre d'exemple, avec , , et , on obtient graphiquement :
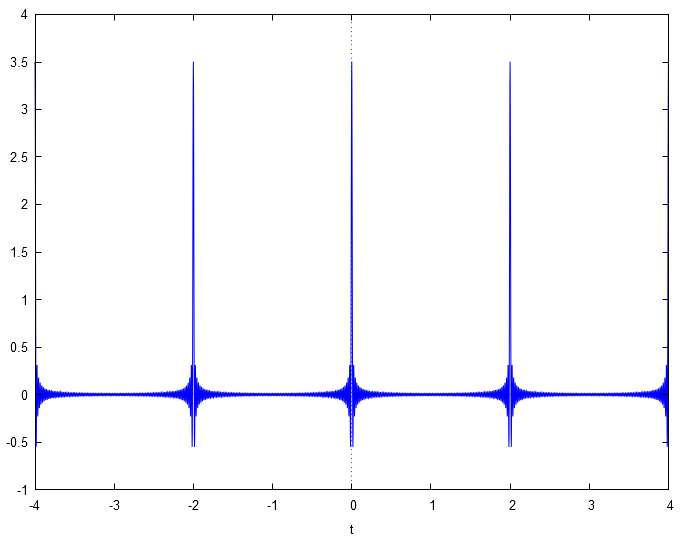
Afin d'obtenir des calculs précis et une démarche rigoureuse, il faut se placer dans le cadre plus général des distibutions (ou fonctions généralisées), introduites par Laurent Schwarz un peu avant 1950. En effet, lorsque , la fonction tend vers un peigne de Dirac. Celui-ci se traite rigoureusement dans le cadre des distributions.
Finalement, on peut simplement dire, à ce stade, que :
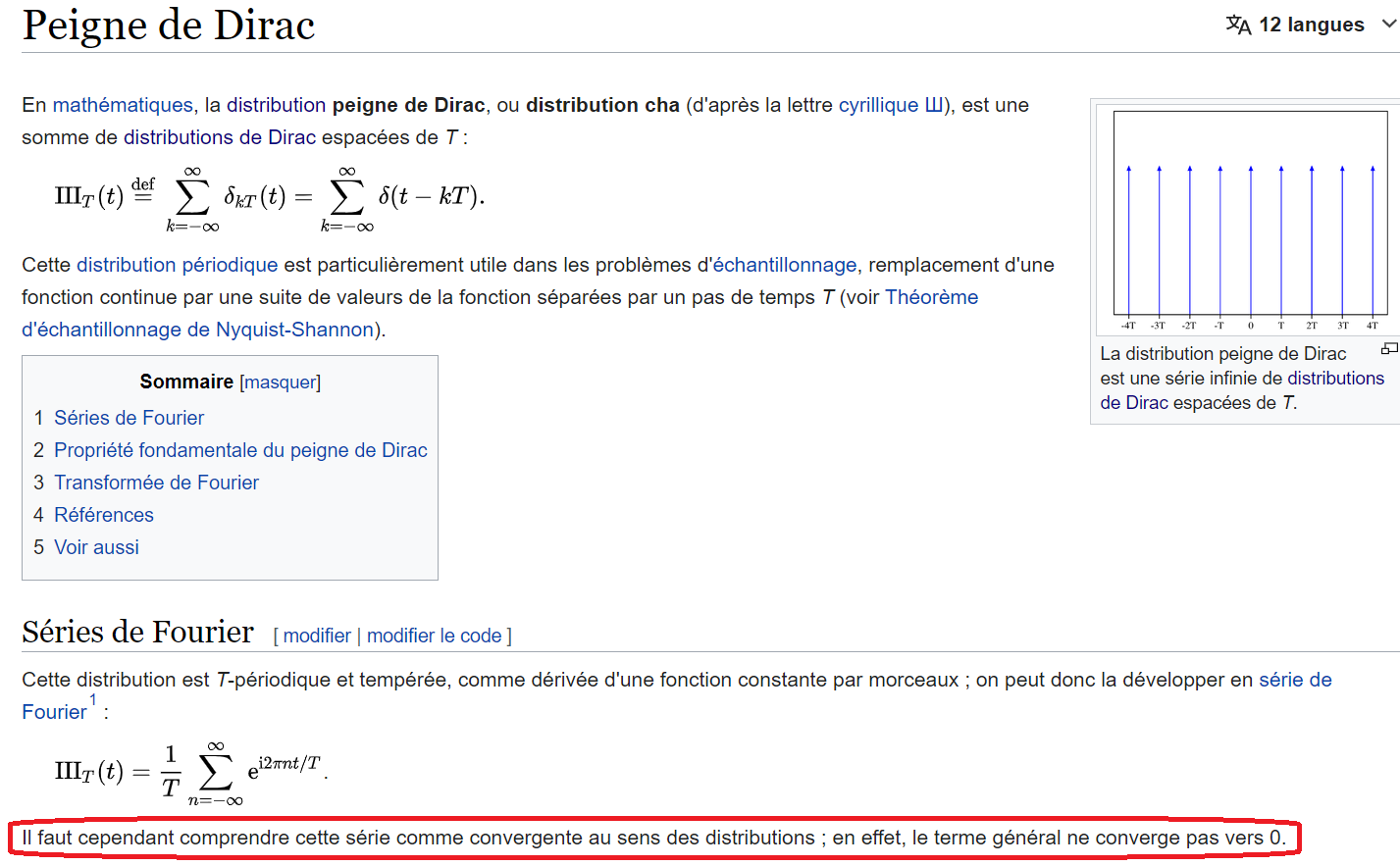
Sur le site d'une encyclopédie en ligne célèbre, on peut y lire :
Soit encore :
Or, on sait que :
Donc, si on pose , on constate que lorsque alors . De fait :
Soit :
Soit encore :
Donc :
La subtilité est dans la somme . En effet, lorsque , cette somme diverge. Afin d'expliquer cela, posons , et on a :
Donc à , on a :
Le terme peut donner un nombre fini non nul lorsque . Lorsque , la fonction est oscillante mais de très faible amplitude. A titre d'exemple, avec , , et , on obtient graphiquement :

Afin d'obtenir des calculs précis et une démarche rigoureuse, il faut se placer dans le cadre plus général des distibutions (ou fonctions généralisées), introduites par Laurent Schwarz un peu avant 1950. En effet, lorsque , la fonction tend vers un peigne de Dirac. Celui-ci se traite rigoureusement dans le cadre des distributions.
Finalement, on peut simplement dire, à ce stade, que :
Sur le site d'une encyclopédie en ligne célèbre, on peut y lire :

Question 13
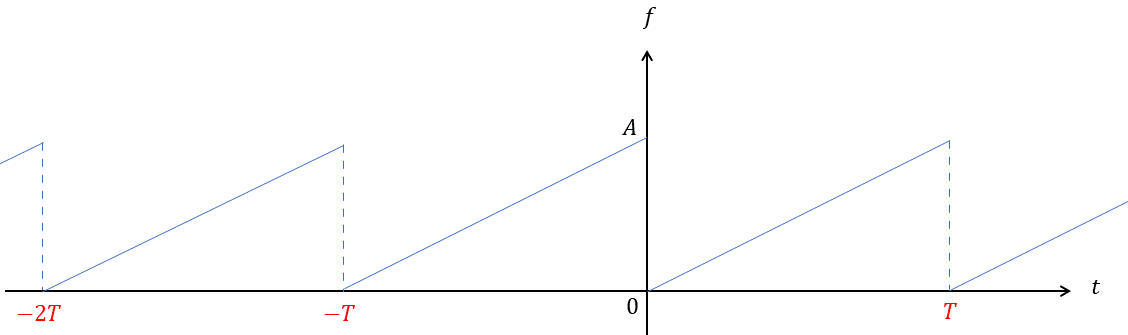
Soit un nombre réel strictement positif. Soit un nombre réel strictement positif. Soit une fonction numérique -périodique, telle que sur l'intervalle :
Représenter graphiquement la fonction .
Correction
On a la représentation graphique suivante :

Question 14
Quelle est la parité de ?
Correction
La fonction est .
Question 15
Déterminer la série de associée.
Correction
On a :
Soit :
D'où :
Puis, avec , on a :
Ce qui nous donne :
A l'aide d'une intégration par parties, on trouve que :
Soit :
Soit encore :
Avec :
Et :
Ainsi, pour , on a :
Ensuite, , on a :
Soit :
A l'aide d'une intégration par parties, on trouve que :
Ce qui nous permet d'écrire que :
Soit encore :
Avec :
Et :
Ce qui nous permet d'écrire que :
Donc :
Ainsi, on a :
Finalement, on aboutit à :
Soit :
D'où :
Puis, avec , on a :
Ce qui nous donne :
A l'aide d'une intégration par parties, on trouve que :
Soit :
Soit encore :
Avec :
Et :
Ainsi, pour , on a :
Ensuite, , on a :
Soit :
A l'aide d'une intégration par parties, on trouve que :
Ce qui nous permet d'écrire que :
Soit encore :
Avec :
Et :
Ce qui nous permet d'écrire que :
Donc :
Ainsi, on a :
Finalement, on aboutit à :
Question 16
Justifier que la série la série de converge bien vers , et préciser la valeur de .
Correction
La fonction . Donc la série converge vers . La valeur de est donnée par la régularisée en ce point. La régularisée vaut :
Finalement :
Finalement :
Question 17
Soit un nombre réel strictement positif. Soit une constante réelle strictement positive. Soit un nombre réel strictement positif. Soit une fonction numérique -périodique, telle que sur l'intervalle :
Représenter graphiquement la fonction dans le cas particulier ou et .
Correction
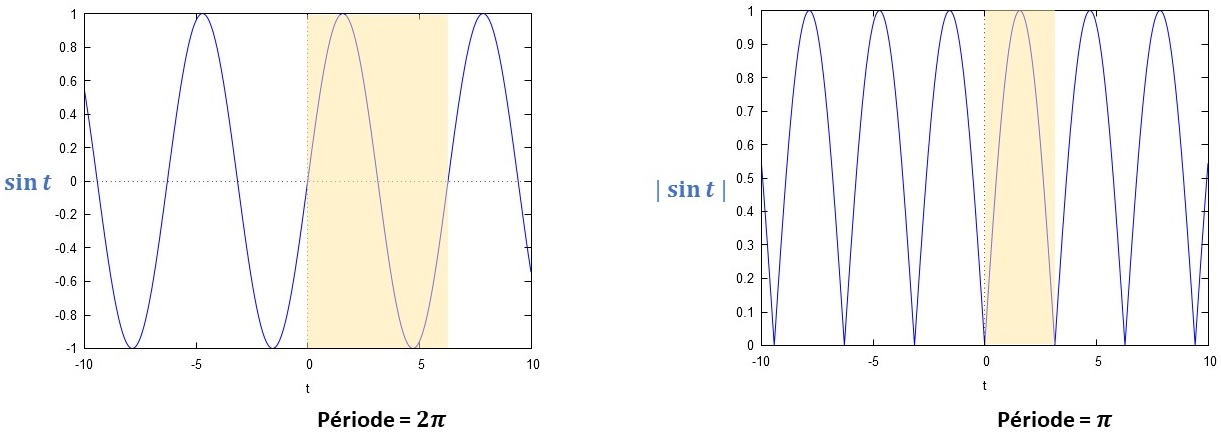
On se place dans le cas particulier ou , et , la fonction a pour image .
On constate que la présence de la valeur absolue modifie la parité. En effet, la fonction sinus est impaire. Cependant la fonction est paire.
De plus, on constate que la présence de la valeur absolue modifie la périodicité {\color{blue}{de moitié}}. En effet, présente un redressement positif de toutes les parties négatives du graphe associé à .
Donc, la période de l'expression est et on en déduit que la période du terme est donnée par :
Graphiquement, cela nous donne :
On constate que la présence de la valeur absolue modifie la parité. En effet, la fonction sinus est impaire. Cependant la fonction est paire.
De plus, on constate que la présence de la valeur absolue modifie la périodicité {\color{blue}{de moitié}}. En effet, présente un redressement positif de toutes les parties négatives du graphe associé à .
Donc, la période de l'expression est et on en déduit que la période du terme est donnée par :
Graphiquement, cela nous donne :

Question 18
Quelle est la parité de ?
Correction
La fonction est .
Question 19
Quelle est la période de ?
Correction
La fonction est de période :
Question 20
Déterminer la série de associée.
Correction
L'expression est paire, donc les coefficients réels sont tous nuls, quelque soit la valeur de .
Le coefficient est quant à lui donné par :
Soit :
D'où :
Enfin, les coefficients réels se déterminent par l'intégrale suivante :
Or, on sait que :
Ainsi, on en déduit que :
Soit :
Soit encore :
La fonction sinus étant impaire, on en déduit alors que :
Ainsi, on peut écrire que :
Soit en intégrant :
Ce qui nous donne encore :
D'où :
Soit encore :
On obtient alors :
Ce qui nous donne au final :
La série de vas donc s'écrire comme :
Finalement :
Le coefficient est quant à lui donné par :
Soit :
D'où :
Enfin, les coefficients réels se déterminent par l'intégrale suivante :
Or, on sait que :
Ainsi, on en déduit que :
Soit :
Soit encore :
La fonction sinus étant impaire, on en déduit alors que :
Ainsi, on peut écrire que :
Soit en intégrant :
Ce qui nous donne encore :
D'où :
Soit encore :
On obtient alors :
Ce qui nous donne au final :
La série de vas donc s'écrire comme :
Finalement :
Question 21
En déduire la valeur numérique de la série suivante :
Correction
La fonction satisfait aux conditions de , et de fait .
Plaçons nous à l'instant . Dans ce cas, on a :
Donc :
Soit :
Soit encore :
Ce qui nous donne :
Ou encore :
Les conditions de permettent d'écrire :
Donc :
En simplifiant par , on obtient :
D'où :
On a alors :
Soit encore :
Finalement, la valeur numérique de la série numérique recherchée est la suivante :
Plaçons nous à l'instant . Dans ce cas, on a :
Donc :
Soit :
Soit encore :
Ce qui nous donne :
Ou encore :
Les conditions de permettent d'écrire :
Donc :
En simplifiant par , on obtient :
D'où :
On a alors :
Soit encore :
Finalement, la valeur numérique de la série numérique recherchée est la suivante :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.