Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 11 - Exercice 1
1 h 30 min
125
L'objectif de cet exercice est la réalisation d'une étude pour comprendre l'apport de la modélisation mathématique pour la description et donc la compréhension d'un phénomène physique.
La thermodynamique apporte en cadre conceptuel macroscopique qui permet de décrire la dynamique engendrée par les échanges thermiques. De part son cadre, elle offre des situations ou en lien avec l'application des Mathématiques.
En mathématiques et en physique théorique, l'équation de la chaleur est une équation aux dérivées partielles parabolique. Elle permet de décrire le phénomène physique de conduction thermique, introduite initialement en 1811 par le mathématicien français Jean Baptiste Joseph Fourier (1768 -1830).

La modélisation de l'évolution de la température a permis d'introduire les séries de Fourier, qui ont apportées une grande amélioration à la modélisation mathématique des phénomènes, en particulier pour les fondements de la thermodynamique, et qui ont entrainé aussi des travaux mathématiques très importants pour les rendre rigoureuses. Ce fut donc une véritable révolution à la fois physique et mathématique, sur plus d'un siècle.
La célèbrissime équation, dite de la chaleur, est la suivante :
où s'appelle le appelle coefficient de diffusivité thermique, et s'exprime en .
:
On envisage un système physique dont l'évolution thermique est unidirectionnelle et donc ne dépend géométriquement que de la variable x.
En outre, lors de l'évolution du champ de température, cette dernière est
et .
La trempe est une opération métallurgique qui fait partie des traitements thermiques. Elle consiste à chauffer un matériau à une température dite de changement de phase ou bien de mise en solution de composés chimiques, selon l'objet de la trempe, pendant le temps nécessaire à la transformation de toute la masse chauffée. Puis à refroidir toute cette masse à une vitesse suffisante pour emprisonner des éléments chimiques qui ont pu se diffuser dans le solide cristallin à haute température lors de la transformation inverse.
Cette technique contribue à l'augmentation de certaines caractéristiques mécaniques de la pièce trempée.
Les avantages sont :
emploi d'acier ordinaire à la place d'acier pour cémentation ;
chauffage très localisé, rapide et économique ;
pas de déformation de la pièce ;
trempe en série sur machine d'induction ;
procédé non polluant.
On considère une plaque métallique rectangulaire de largeur de longueur et d'épaisseur . Cette plaque est et amenée à la température . La direction de la longueur sera celle des abscisses . L'origine géométrique est indiquée sur le schéma ci-dessous :

Afin de lui faire subir une trempe, elle va être plongée (par roulement et basculement), dans de l'eau (par sa petite surface ) à la température inférieure à . L'instant de la trempe sera considéré comme origine des temps .
On introduit les deux grandeurs sans dimension, et , suivantes :
Ainsi on définit la fonction de la manière suivante :
La thermodynamique apporte en cadre conceptuel macroscopique qui permet de décrire la dynamique engendrée par les échanges thermiques. De part son cadre, elle offre des situations ou en lien avec l'application des Mathématiques.
En mathématiques et en physique théorique, l'équation de la chaleur est une équation aux dérivées partielles parabolique. Elle permet de décrire le phénomène physique de conduction thermique, introduite initialement en 1811 par le mathématicien français Jean Baptiste Joseph Fourier (1768 -1830).

La modélisation de l'évolution de la température a permis d'introduire les séries de Fourier, qui ont apportées une grande amélioration à la modélisation mathématique des phénomènes, en particulier pour les fondements de la thermodynamique, et qui ont entrainé aussi des travaux mathématiques très importants pour les rendre rigoureuses. Ce fut donc une véritable révolution à la fois physique et mathématique, sur plus d'un siècle.
La célèbrissime équation, dite de la chaleur, est la suivante :
où s'appelle le appelle coefficient de diffusivité thermique, et s'exprime en .
:
On envisage un système physique dont l'évolution thermique est unidirectionnelle et donc ne dépend géométriquement que de la variable x.
En outre, lors de l'évolution du champ de température, cette dernière est
et .
La trempe est une opération métallurgique qui fait partie des traitements thermiques. Elle consiste à chauffer un matériau à une température dite de changement de phase ou bien de mise en solution de composés chimiques, selon l'objet de la trempe, pendant le temps nécessaire à la transformation de toute la masse chauffée. Puis à refroidir toute cette masse à une vitesse suffisante pour emprisonner des éléments chimiques qui ont pu se diffuser dans le solide cristallin à haute température lors de la transformation inverse.
Cette technique contribue à l'augmentation de certaines caractéristiques mécaniques de la pièce trempée.
Les avantages sont :
emploi d'acier ordinaire à la place d'acier pour cémentation ;
chauffage très localisé, rapide et économique ;
pas de déformation de la pièce ;
trempe en série sur machine d'induction ;
procédé non polluant.
On considère une plaque métallique rectangulaire de largeur de longueur et d'épaisseur . Cette plaque est et amenée à la température . La direction de la longueur sera celle des abscisses . L'origine géométrique est indiquée sur le schéma ci-dessous :

Afin de lui faire subir une trempe, elle va être plongée (par roulement et basculement), dans de l'eau (par sa petite surface ) à la température inférieure à . L'instant de la trempe sera considéré comme origine des temps .
On introduit les deux grandeurs sans dimension, et , suivantes :
Ainsi on définit la fonction de la manière suivante :
Question 1
" la Théorie de la Chaleur de Fourier est un des premiers exemples d'application de l'analyse à la physique [...]. Les résultats qu'il a obtenus sont certes intéressants par eux-mêmes, mais ce qui l'est plus encore est la méthode qu'il a employée pour y parvenir et qui servira toujours de modèle à tous ceux qui voudront cultiver une branche quelconque de la physique mathématique."

Écrire l'équation de la chaleur vérifiée par la fonction température .
Correction
L'équation de la chaleur vérifiée par la fonction température est :
Elle est associée à la figure suivante :
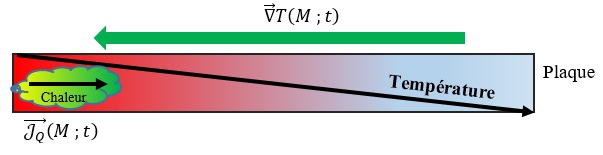
Elle est associée à la figure suivante :

Question 2
Interrogez-vous sur les éléments de vocabulaire présents dans les hypothèses.
Correction
Les éléments de vocabulaire qui sont présents dans les sont :
: Les conditions de bord (dit en bain thermique) ainsi que la symétrie de la plaque, implique une propagation uniquement dans la direction . La direction de l'augmentation de la température (est celle du gradient de température) et est opposée à celle du flux thermique. C'est ceci qui explique le signe dans la loi phénoménologique de \textit{Fourier}.
: La décroissance de la température, au fur et à mesure que le temps s'écoule, est prise en compte dans la modélisation.
: La température, en chaque instant et en chaque endroit géométrique de la plaque, à une valeur réelle différente de l'infinie. Physiquement, la température est minorée par et majorée par . Ainsi la température est bien « encadrée », on dit qu'elle est bornée. En ce qui concerne la température adimensionnée, on a ; donc elle est bornée également.
: Les conditions de bord (dit en bain thermique) ainsi que la symétrie de la plaque, implique une propagation uniquement dans la direction . La direction de l'augmentation de la température (est celle du gradient de température) et est opposée à celle du flux thermique. C'est ceci qui explique le signe dans la loi phénoménologique de \textit{Fourier}.
: La décroissance de la température, au fur et à mesure que le temps s'écoule, est prise en compte dans la modélisation.
: La température, en chaque instant et en chaque endroit géométrique de la plaque, à une valeur réelle différente de l'infinie. Physiquement, la température est minorée par et majorée par . Ainsi la température est bien « encadrée », on dit qu'elle est bornée. En ce qui concerne la température adimensionnée, on a ; donc elle est bornée également.
Question 3
Interrogez-vous sur l'intérêt d'introduire des variables sans dimension.
Correction
L'intérêt d'introduire des variables sans dimensions est de pouvoir trouver des solutions qui ne dépendent pas des caractéristiques physiques de la plaque. Ainsi, pour cette géométrie, les variables sans dimensions permettent d'écrire des solutions universelles, et qui sont graphiquement représentables et valables, indépendamment des distances et des valeurs de températures.
Question 4
En considérant un plan transversal rectangulaire , avec , justifier que la fonction adimensionnée y soit uniforme.
Correction
La barre chauffée chute brutalement dans de l'eau plus froide. Elle est donc totalement immergée dans l'eau froide. Ainsi, par symétrie, ce refroidissement s'effectue de façon identique sur la frontière d'un plan transversal rectangulaire , avec , De ceci, on en déduit que la température y sera uniforme à l'intérieur de ce plan. Et de ce fait, la fonction adimensionnée y soit également uniforme.
Question 5
Écrire l'équation de la chaleur vérifiée par la fonction adimensionnée .
Correction
On a :
D'où :
Et :
Ainsi, l'équation de la chaleur devient :
Finalement l'équation de la chaleur, vérifiée par la fonction adimensionnée , est :
D'où :
Et :
Ainsi, l'équation de la chaleur devient :
Finalement l'équation de la chaleur, vérifiée par la fonction adimensionnée , est :
Question 6
Justifier de la périodicité spatiale de la fonction dans la direction des abscisses.
Correction
Les conditions de bords aux abscisses et , qui sont , ou encore , impliquent la périodicité spatiale de la fonction dans la direction des abscisses.
Question 7
Justifier de l'emploi de la méthode dite dans cette situation.
Correction
La périodicité spatiale est indépendante du temps (comme le montre la question précédente), donc la \textit{méthode des variables séparées} est dans cette situation une démarche intellectuelle pertinente. Dans ce cas, on posera : .
Question 8
Démontrer que la température dans la plaque se modélise par l'expression :
Correction
L'équation vérifiée par prend la forme suivante :
En divisant par on trouve que :
Les deux membres dépendant de deux variables différentes, l'unique possibilité pour avoir une égalité est que chacun soit égale à une constante . On a alors :
Ce qui nous donne :
La périodicité spatiale implique nécessairement d'avoir des solutions qui soient périodiques. De ce fait, la seule possibilité est d'avoir . C'est pourquoi on pose avec . Donc, on obtient :
L'équation de est une équation différentielle du deuxième ordre, homogène et à coefficients constants. Les solutions sont évidentes et s'écrivent, avec :
Or, on a . Ainsi on en déduit que :
D'où :
Ce qui implique :
Ainsi :
Puis, la condition nous permet d'écrire :
Ainsi, on en déduit que :
D'où :
En un instant donné, la température de la plaque, en son plan médian, donc en est nécessairement différente de . Autrement dit la température adimensionnée ne sera pas nulle dans le plan médian (elle y sera d'ailleurs maximale). Ainsi, on en déduit que :
Comme doit être non nul, sinon, il n'y aura jamais de phénomène périodique, on en déduit que :
D'où :
D'où :
Dès lors, on peut écrire que :
L'équation de est une équation différentielle du premier ordre, homogène et à coefficients constants. Les solutions sont évidentes et s'écrivent, avec :
Ce qui implique que la température adimensionnée prenne la forme mathématique suivante :
Or, l'équation que vérifie est , donc une combinaison linéaire des formes mathématiques précédentes est toujours solution. Ce qui revient à « balayer » toutes les valeurs de possible. Pour une valeur de donnée, la solution s'appelle . De ce fait, la solution globale est de la forme :
Il ne reste plus qu'à déterminer l'expression des coefficients . Pour faire cela, on va se souvenir qu'à l'instant initial , la température est en chaque endroit de la plaque est , soit, , on obtient : . Ceci nous permet d'écrire (avec ) :
On reconnait une série de associée . Cette dernière ne fait apparaître que la contribution des sinus, donc .
Il nous reste à déterminer la période spatiale associée à cette propagation de chaleur. On a une situation du type :

Ceci implique que la périodicité spatiale est égale au double de la longueur de la plaque, à savoir , donc la demi-période est la longueur de la barre elle même . Ce qui nous permet d'écrire :
Soit encore :
D'où :
Ainsi, on obtient :
On peut donc écrire que :
Or, on sait que , donc :
On peut donc écrire que :
Finalement, on a bien démontrer que la température dans la plaque se modélise par l'expression :
En divisant par on trouve que :
Les deux membres dépendant de deux variables différentes, l'unique possibilité pour avoir une égalité est que chacun soit égale à une constante . On a alors :
Ce qui nous donne :
La périodicité spatiale implique nécessairement d'avoir des solutions qui soient périodiques. De ce fait, la seule possibilité est d'avoir . C'est pourquoi on pose avec . Donc, on obtient :
L'équation de est une équation différentielle du deuxième ordre, homogène et à coefficients constants. Les solutions sont évidentes et s'écrivent, avec :
Or, on a . Ainsi on en déduit que :
D'où :
Ce qui implique :
Ainsi :
Puis, la condition nous permet d'écrire :
Ainsi, on en déduit que :
D'où :
En un instant donné, la température de la plaque, en son plan médian, donc en est nécessairement différente de . Autrement dit la température adimensionnée ne sera pas nulle dans le plan médian (elle y sera d'ailleurs maximale). Ainsi, on en déduit que :
Comme doit être non nul, sinon, il n'y aura jamais de phénomène périodique, on en déduit que :
D'où :
D'où :
Dès lors, on peut écrire que :
L'équation de est une équation différentielle du premier ordre, homogène et à coefficients constants. Les solutions sont évidentes et s'écrivent, avec :
Ce qui implique que la température adimensionnée prenne la forme mathématique suivante :
Or, l'équation que vérifie est , donc une combinaison linéaire des formes mathématiques précédentes est toujours solution. Ce qui revient à « balayer » toutes les valeurs de possible. Pour une valeur de donnée, la solution s'appelle . De ce fait, la solution globale est de la forme :
Il ne reste plus qu'à déterminer l'expression des coefficients . Pour faire cela, on va se souvenir qu'à l'instant initial , la température est en chaque endroit de la plaque est , soit, , on obtient : . Ceci nous permet d'écrire (avec ) :
On reconnait une série de associée . Cette dernière ne fait apparaître que la contribution des sinus, donc .
Il nous reste à déterminer la période spatiale associée à cette propagation de chaleur. On a une situation du type :

Ceci implique que la périodicité spatiale est égale au double de la longueur de la plaque, à savoir , donc la demi-période est la longueur de la barre elle même . Ce qui nous permet d'écrire :
Soit encore :
D'où :
Ainsi, on obtient :
On peut donc écrire que :
Or, on sait que , donc :
On peut donc écrire que :
Finalement, on a bien démontrer que la température dans la plaque se modélise par l'expression :
Question 9
Interpréter et analyser votre résultat. L'usage d'un logiciel de représentation graphique (du type , , , , , , ou tout autre) de la grandeur peut s'avérer pertinent. Pour cela vous définirez un temps caractéristique (donc qui a les dimensions d'un temps), puis vous poserez la grandeur adimensionnée suivante :
Correction
Pour interpréter et analyser ce résultat, il faut utiliser les variable réduite, ainsi on s'affranchit de la géométrie particulière de la plaque étudiée.
C'est pourquoi il faut introduire une distance sans dimension, notée , ainsi qu'en temps également sans dimension, noté quant à lui .
En ce qui concerne la distance, on pose (car est une distance caractéristique de la géométrie de la propagation au sein de la plaque):
En ce qui concerne un temps caractéristique de la propagation au sein de la plaque, il suffit de se souvenir qu'une exponentielle est . On en déduit alors que :
Donc un temps sans dimension caractéristique de cette propagation de chaleur est :
Ce qui nous donne donc :
: (parfaitement symétrique par rapport au milieu de barre) :

: (parfaitement symétrique par rapport au milieu de barre) :
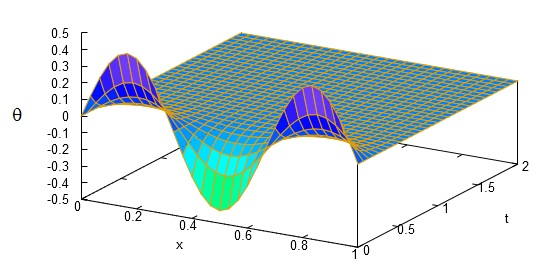
(parfaitement symétrique par rapport au milieu de barre et comprise entre 0 et 1) et mettant clairement en évidence un comportement plus « collectifs » des modes de propagations :
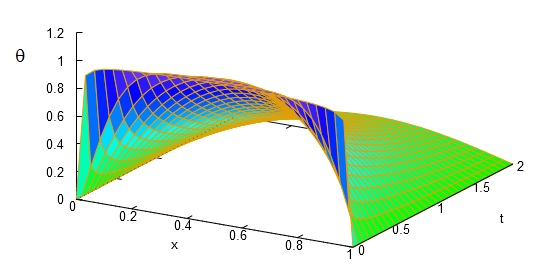
(parfaitement symétrique par rapport au milieu de barre et comprise entre 0 et 1) et mettant clairement en évidence un comportement plus « collectifs » des modes de propagations :
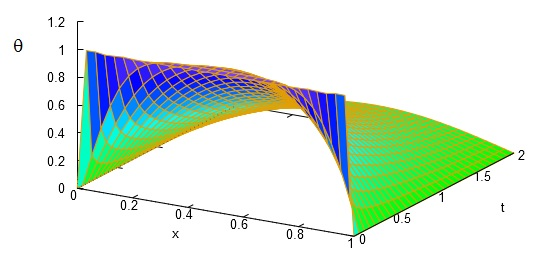
Le comportement limite en créneau (exponentiellement décroissant temporellement) est confirmé. Nous sommes aux limites thermoélastiques physiquement possibles pour une barre de métal surchauffée. Cela peut se confirmer visuellement sur la photo du sujet : couleur (quasi uniforme) dans le plan de face.
Les harmoniques des ordres élevés disparaissent quasiment immédiatement et seul le mode fondamental perdure en .
C'est pourquoi il faut introduire une distance sans dimension, notée , ainsi qu'en temps également sans dimension, noté quant à lui .
En ce qui concerne la distance, on pose (car est une distance caractéristique de la géométrie de la propagation au sein de la plaque):
En ce qui concerne un temps caractéristique de la propagation au sein de la plaque, il suffit de se souvenir qu'une exponentielle est . On en déduit alors que :
Donc un temps sans dimension caractéristique de cette propagation de chaleur est :
Ce qui nous donne donc :
: (parfaitement symétrique par rapport au milieu de barre) :

: (parfaitement symétrique par rapport au milieu de barre) :

(parfaitement symétrique par rapport au milieu de barre et comprise entre 0 et 1) et mettant clairement en évidence un comportement plus « collectifs » des modes de propagations :

(parfaitement symétrique par rapport au milieu de barre et comprise entre 0 et 1) et mettant clairement en évidence un comportement plus « collectifs » des modes de propagations :

Le comportement limite en créneau (exponentiellement décroissant temporellement) est confirmé. Nous sommes aux limites thermoélastiques physiquement possibles pour une barre de métal surchauffée. Cela peut se confirmer visuellement sur la photo du sujet : couleur (quasi uniforme) dans le plan de face.
Les harmoniques des ordres élevés disparaissent quasiment immédiatement et seul le mode fondamental perdure en .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.