Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 10 - Exercice 1
2 h
165
Une application importante des séries de Fourier aux phénomènes vibratoires en Physique?
Question 1
On appelle , l'quation aux érivées artielles (E.D.P.) suivante :
On parle, historiquement, , et elle fut établie en 1746 par le mathématicien français .
On se propose de chercher, sur le domaine , les solutions bornées qui satisfaisont aux conditions :
limites : ;
initiales : et .
Ce problème décrit, à chaque instant , les mouvements transversaux d'une corde homogène, tendue, de longueur . L'élongation de chaque point d'abscisse est notée, à l'instant , par .
La corde est fixée à ses extrémités et on néglige la force de pesanteur terrestre devant la force de tension de la corde, ainsi que toutes formes d'amortissement du mouvement.
A l'instant initial , la corde à une forme décrite par et chaque point de cette corde est libérée à une vitesse verticale initiale donnée, quant à elle, par .
On parle, historiquement, , et elle fut établie en 1746 par le mathématicien français .
On se propose de chercher, sur le domaine , les solutions bornées qui satisfaisont aux conditions :
limites : ;
initiales : et .
Ce problème décrit, à chaque instant , les mouvements transversaux d'une corde homogène, tendue, de longueur . L'élongation de chaque point d'abscisse est notée, à l'instant , par .
La corde est fixée à ses extrémités et on néglige la force de pesanteur terrestre devant la force de tension de la corde, ainsi que toutes formes d'amortissement du mouvement.
A l'instant initial , la corde à une forme décrite par et chaque point de cette corde est libérée à une vitesse verticale initiale donnée, quant à elle, par .
Résoudre l'équation des ondes par la méthode dite des variables séparées, à savoir, on pose .
Correction
On pose , dans ce cas l'équation des ondes devient :
Soit :
Soit encore :
D'où :
Cette égalité porte sur des expressions dont les variables sont différentes. C'est pourquoi, pour que cette dernière égalité soit possible, est que chacun des deux membres . Posons cette constante réelle. On a alors :
Ce qui nous donne :
A ce stade, deux réflexions s'imposent :
, pour décrire des phénomènes oscillants et vibratoires, il est nécessaire de faire appelle aux fonctions trigonométriques sinus et cosinus. , ces fonctions doivent donc être les solutions de ces deux équations différentielles. Ceci impose donc que la constante réelle soit strictement négative : .
Afin d'être homogène vis-à-vis du terme qui multiplie , il est plus pratique d'exprimer la constante réelle .
C'est pourquoi, on pose :
Ce qui nous donne :
Avec .
Les conditions limites s'expriment comme :
Ce qui implique que :
Or, on sait que , avec . Ce qui implique :
Comme dépend de l'entier naturel , on parle alors de . C'est pourquoi, on marque cette quantification par l'écriture . Ainsi, à ce stade, la solution recherchée prend la forme :
Soit encore, avec :
avec et pour indiquer la quantification qui régit ce phénomène vibratoire.
Soit :
Soit encore :
D'où :
Cette égalité porte sur des expressions dont les variables sont différentes. C'est pourquoi, pour que cette dernière égalité soit possible, est que chacun des deux membres . Posons cette constante réelle. On a alors :
Ce qui nous donne :
A ce stade, deux réflexions s'imposent :
, pour décrire des phénomènes oscillants et vibratoires, il est nécessaire de faire appelle aux fonctions trigonométriques sinus et cosinus. , ces fonctions doivent donc être les solutions de ces deux équations différentielles. Ceci impose donc que la constante réelle soit strictement négative : .
Afin d'être homogène vis-à-vis du terme qui multiplie , il est plus pratique d'exprimer la constante réelle .
C'est pourquoi, on pose :
Ce qui nous donne :
Avec .
Les conditions limites s'expriment comme :
Ce qui implique que :
Or, on sait que , avec . Ce qui implique :
Comme dépend de l'entier naturel , on parle alors de . C'est pourquoi, on marque cette quantification par l'écriture . Ainsi, à ce stade, la solution recherchée prend la forme :
Soit encore, avec :
avec et pour indiquer la quantification qui régit ce phénomène vibratoire.
Question 2
Montrer que la solution à ce problème (conditions limites et initiales incluses) est donnée par l'expression :
Expliciter clairement les expressions des deux coefficients réels et .
Expliciter clairement les expressions des deux coefficients réels et .
Correction
Pour chaque valeur de l'entier naturel non nul, il correspond une manière de vibrer pour la corde. On parle de de vibrations. Donc .
Mathématiquement, c'est la linéarité de l'E.D.P. des ondes qui permet cette sommation des solutions. Avec , ceci s'exprime comme :
où . En posant et , on peut finalement écrire que :
Les deux conditions initiales, et , nous permettent d'écrire respectivement :
Déterminons l'expression des coefficients réels avec . On a, avec et :
En intégrant sur toute la longueur de la corde, on obtient :
L'intégration portant sur et la sommation sur , et sous réserve de la convergence (uniforme) de la série, on va donc pouvoir permuter ces deux opérations. On a alors :
Deux situations sont à envisager : soit , soit .
.
On a :
Avec :
Ce qui nous donne :
Soit :
.
On a :
Avec :
Soit :
Pour conclure cette détermination d'intégrale, on introduit le symbole "delta" de ( :
Ainsi :
En conclusion, on a :
Ceci nous permet d'écrire que :
Ce qui nous donne :
La fonction {\color{blue}{ est -périodique et impaire}}, et ce coefficient peut encore être écrit sous la forme :
Puis, en exploitant la condition :
On trouve par un raisonnement totalement similaire que :
ou encore :
La fonction {\color{blue}{ est -périodique et impaire}}, et ce coefficient peut encore être écrit sous la forme :
Finalement la solution analytique générale de l'équation des ondes est donnée par la belle expression suivante :
Mathématiquement, c'est la linéarité de l'E.D.P. des ondes qui permet cette sommation des solutions. Avec , ceci s'exprime comme :
où . En posant et , on peut finalement écrire que :
Les deux conditions initiales, et , nous permettent d'écrire respectivement :
Déterminons l'expression des coefficients réels avec . On a, avec et :
En intégrant sur toute la longueur de la corde, on obtient :
L'intégration portant sur et la sommation sur , et sous réserve de la convergence (uniforme) de la série, on va donc pouvoir permuter ces deux opérations. On a alors :
Deux situations sont à envisager : soit , soit .
.
On a :
Avec :
Ce qui nous donne :
Soit :
.
On a :
Avec :
Soit :
Pour conclure cette détermination d'intégrale, on introduit le symbole "delta" de ( :
Ainsi :
En conclusion, on a :
Ceci nous permet d'écrire que :
Ce qui nous donne :
La fonction {\color{blue}{ est -périodique et impaire}}, et ce coefficient peut encore être écrit sous la forme :
Puis, en exploitant la condition :
On trouve par un raisonnement totalement similaire que :
ou encore :
La fonction {\color{blue}{ est -périodique et impaire}}, et ce coefficient peut encore être écrit sous la forme :
Finalement la solution analytique générale de l'équation des ondes est donnée par la belle expression suivante :
Question 3
Une corde de piano, initialement rectiligne, donc satisfaisant à : .
Elle est alors frappée avec un petit marteau de manière à communiquer aux points de la corde compris entre les abscisses et , avec , une vitesse initiale constante .
On a donc :
Déterminer la solution associée à cette corde de piano.
Elle est alors frappée avec un petit marteau de manière à communiquer aux points de la corde compris entre les abscisses et , avec , une vitesse initiale constante .

On a donc :
Déterminer la solution associée à cette corde de piano.
Correction
Par hypothèse, on sait que , donc tous les coefficients , avec sont nuls.
En ce qui concerne les coefficients réels , on a :
Soit :
Ainsi, on obtient :
D'où :
Soit :
La forme de la corde est donc donnée par la série suivante :
Mais on peut en trouver une expression simplifiée car on a l'hypothèse . Dans ce cas, on peut écrire que :
Ce qui nous donne :
Ce dernier résultat pouvait se retrouver directement à partir de la définition de . En effet :
Or, entre et , l'expression à intégrer est quasiment égale à car elle n'a pas le temps de beaucoup varier (le physicien parle de . Ainsi, on obtient :
Ce qui nous redonne bien :
Finalement, on trouve que la forme approchée de la corde est donnée par la série suivante :
En ce qui concerne les coefficients réels , on a :
Soit :
Ainsi, on obtient :
D'où :
Soit :
La forme de la corde est donc donnée par la série suivante :
Mais on peut en trouver une expression simplifiée car on a l'hypothèse . Dans ce cas, on peut écrire que :
Ce qui nous donne :
Ce dernier résultat pouvait se retrouver directement à partir de la définition de . En effet :
Or, entre et , l'expression à intégrer est quasiment égale à car elle n'a pas le temps de beaucoup varier (le physicien parle de . Ainsi, on obtient :
Ce qui nous redonne bien :
Finalement, on trouve que la forme approchée de la corde est donnée par la série suivante :
Question 4
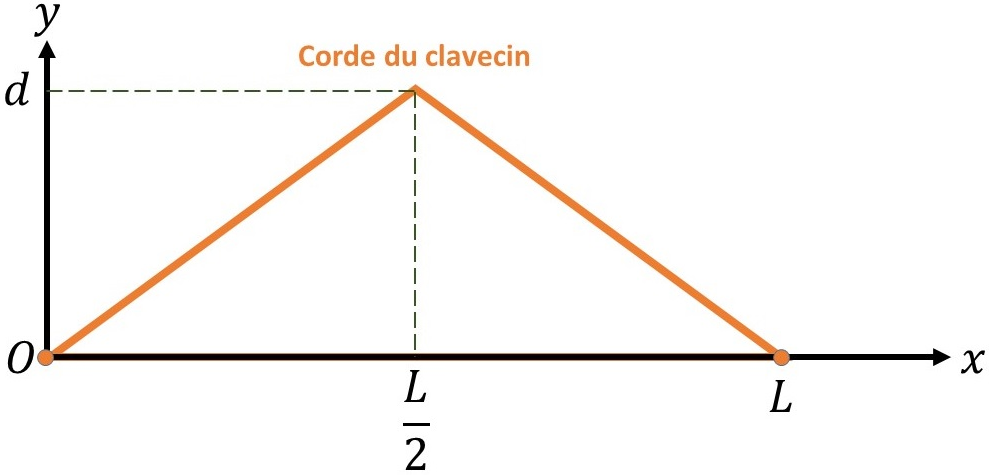
Même question dans le cas d'une corde de clavecin pincée en son milieu, à sans vitesse initiale, comme l'indique la figure suivante :

Correction
A , la corde est lâchée sans vitesse initiale, ce qui implique que et de fait ().
Puis, on a :
Ce qui nous donne :
Soit :
Chacune de ces deux intégrales se déterminent par une I.P.P., on trouve alors :
Avec :
Ce qui nous donne :
Puis, on a :
Ce qui nous donne :
Soit :
Chacune de ces deux intégrales se déterminent par une I.P.P., on trouve alors :
Avec :
Ce qui nous donne :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.