Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 1 - Exercice 1
30 min
45
On note par le nombre complexe tel que .
On appelle série trigonométrique, à valeurs dans ou , une série de fonctions d'une variable réelle de la forme :
Et et sont des suites de nombres réels ou complexes.
On a les propriétés suivantes :
- si une série trigonométrique est convergente, alors sa somme est une fonction -périodique ;
- si ou n'est pas nul alors la plus petite période de la fonction définie par la somme d'une série trigonométrique convergente est ;
- si tous les coefficients sont nuls, alors la somme d'une série trigonométrique convergente est une fonction paire ;
- si tous les coefficients sont nuls, alors la somme d'une série trigonométrique convergente est une fonction impaire ;
- Il existe une forme complexe équivalente :
avec et pour , on a d'une part , et d'autre part
On peut donc, facilement, passer d'une formulation réelle à une formulation complexe et inversement. En effet, on a mis également :
Soit une fonction d'une variable réelle à valeur réelles ou complexes, qui est - périodique et continues par morceaux.
On appelle de les nombres, réels ou complexes suivants :
On appelle de les nombres complexes suivants :
On appelle de la série de fonction suivante :
- Remarque 1 : les fonctions intégrées étant -périodique, il est possible de remplacer l'intervalle d'intégration par n'importe quel autre intervalle de longueur . Dans la cas d'une fonction paire ou impaire il peut être judicieux de faire usage de l'intervalle d'intégration .
- Remarque 2 : La série de Fourier peut également s'écrire avec les coefficient et son expression est .
- Remarque 3 : Les diverses hypothèses faites sur la fonction impliquent que la série de Fourier existe bien. Néanmoins sa convergence c'est pas assurée et de plus rien n'assure que la somme associée soit égale à .
Soit une fonction continue et définie sur et à valeurs dans ou , -périodique et de classe par morceaux. On désigne par la fonction dérivée première associée. On a alors :
Puis :
On déduit de ce théorème que si une fonction est de classe par morceaux, ces coefficients de Fourier tendent vers lorsque tend vers l'infini.
Remarque :
Si est -périodique et de classe alors ses coefficients de Fourier sont des .
En effet, si est -périodique et de classe alors on a l'intégration ci-dessous :
En faisant usage de la méthode de l'intégration par parties, on obtient :
Soit :
Comme est -périodique, on en déduit que . Ainsi :
Puis, par récurrence, avec , on obtient directement :
Ce qui implique que :
Or, lorsque on a . Ceci permet de conclure que .
Soit une fonction numérique -périodique d'une variable réelle et à valeurs réelles ou complexes. Si cette fonction est par morceaux alors la série de Fourier est simplement convergente sur et sa somme est égale, en , à la demi-somme des limites à gauche et à droite de . Cette demi-somme s'appelle la régularisée de en et se note parfois . On a donc :
Et :
Et bien évidemment, on a de manière équivalente :
Et :
ainsi que
On dit qu'une fonction définie sur et à valeur réelles ou complexes vérifie les conditions du mathématicien prusse Johann Peter Gustav Lejeune Dirichlet (1805 - 1859) si les trois conditions suivantes sont satisfaites simultanément :
- la fonction est -périodique ;
- la fonction est (c'est à dire continue) par morceaux ;
- la valeur de en tout point est égale à la régularisée .
L'ensemble des fonctions qui vérifient les conditions de Dirichlet est un sous-espace vectoriel de l'espace vectoriel des fonctions numériques univariées définies sur ou ; ou celui des fonctions numériques univariées -périodique. Cet ensemble se note par .
La série de Fourier de toute fonction appartenant à l'ensemble qui est de classe par morceaux est, sur , simplement convergente.
On définit sur l'ensemble une forme bilinéaire de la manière suivante :
L'ensemble munie de la forme bilinéaire est un espace pré-hilbertient (complexe)
On désigne par la famille des éléments de l'ensemble de Dirichlet qui sont définis par :
Et on a les deux propriétés suivantes :
- la famille est une famille orthonormale de l'espace ;
- pour tout nombre entier naturel , le coefficient de Fourier d'une fonction de est égal au produit hermitien .
Soit une fonction numérique univariée de dans ou , -périodique, continue sur et de classe par morceaux. Dans ce cas la série de Fourier de la fonction converge normalement, sur , vers .
Si la famille est une famille orthonormale d'un espace pré-hilbertien quelconque alors, pour on a l'inégalité, dite de Bessel, suivante :
En appliquant cette inégalité à l'espace aux cas des deux suites et des coefficient de Fourier de alors les deux séries numériques et sont convergentes.
Lorsque l'espace pré-hilbertien est il existe le théorème mathématicien français Marc-Antoine Parseval des Chênes (1755-1836) qui est plus puissant que l'inégalité de Bessel : ce n'est plus une inégalité mais une égalité.
Pour toute fonction on a l'égalité suivante :
Et :
Remarque :
Soit un nombre réel strictement positif. Dans le cas des fonctions -périodique on a les définitions suivantes des coefficient de Fourier :
On rappelle qu'une fonction numérique univariée définie sur un ensemble est déclarée de période , ou -périodique, si elle vérifie :
Lorsqu'une fonction est périodique, son graphe reproduit de façon répétitive n’importe quelle portion particulière de longueur égale à une période : c'est une propriété d'invariance par translation.
La série de Fourier associée à , c'est-à-dire le développement trigonométrique ou exponentielle est couramment désigné par .
On appelle série trigonométrique, à valeurs dans ou , une série de fonctions d'une variable réelle de la forme :
Et et sont des suites de nombres réels ou complexes.
On a les propriétés suivantes :
- si une série trigonométrique est convergente, alors sa somme est une fonction -périodique ;
- si ou n'est pas nul alors la plus petite période de la fonction définie par la somme d'une série trigonométrique convergente est ;
- si tous les coefficients sont nuls, alors la somme d'une série trigonométrique convergente est une fonction paire ;
- si tous les coefficients sont nuls, alors la somme d'une série trigonométrique convergente est une fonction impaire ;
- Il existe une forme complexe équivalente :
avec et pour , on a d'une part , et d'autre part
On peut donc, facilement, passer d'une formulation réelle à une formulation complexe et inversement. En effet, on a mis également :
Soit une fonction d'une variable réelle à valeur réelles ou complexes, qui est - périodique et continues par morceaux.
On appelle de les nombres, réels ou complexes suivants :
On appelle de les nombres complexes suivants :
On appelle de la série de fonction suivante :
- Remarque 1 : les fonctions intégrées étant -périodique, il est possible de remplacer l'intervalle d'intégration par n'importe quel autre intervalle de longueur . Dans la cas d'une fonction paire ou impaire il peut être judicieux de faire usage de l'intervalle d'intégration .
- Remarque 2 : La série de Fourier peut également s'écrire avec les coefficient et son expression est .
- Remarque 3 : Les diverses hypothèses faites sur la fonction impliquent que la série de Fourier existe bien. Néanmoins sa convergence c'est pas assurée et de plus rien n'assure que la somme associée soit égale à .
Soit une fonction continue et définie sur et à valeurs dans ou , -périodique et de classe par morceaux. On désigne par la fonction dérivée première associée. On a alors :
Puis :
On déduit de ce théorème que si une fonction est de classe par morceaux, ces coefficients de Fourier tendent vers lorsque tend vers l'infini.
Remarque :
Si est -périodique et de classe alors ses coefficients de Fourier sont des .
En effet, si est -périodique et de classe alors on a l'intégration ci-dessous :
En faisant usage de la méthode de l'intégration par parties, on obtient :
Soit :
Comme est -périodique, on en déduit que . Ainsi :
Puis, par récurrence, avec , on obtient directement :
Ce qui implique que :
Or, lorsque on a . Ceci permet de conclure que .
Soit une fonction numérique -périodique d'une variable réelle et à valeurs réelles ou complexes. Si cette fonction est par morceaux alors la série de Fourier est simplement convergente sur et sa somme est égale, en , à la demi-somme des limites à gauche et à droite de . Cette demi-somme s'appelle la régularisée de en et se note parfois . On a donc :
Et :
Et bien évidemment, on a de manière équivalente :
Et :
ainsi que
On dit qu'une fonction définie sur et à valeur réelles ou complexes vérifie les conditions du mathématicien prusse Johann Peter Gustav Lejeune Dirichlet (1805 - 1859) si les trois conditions suivantes sont satisfaites simultanément :
- la fonction est -périodique ;
- la fonction est (c'est à dire continue) par morceaux ;
- la valeur de en tout point est égale à la régularisée .
L'ensemble des fonctions qui vérifient les conditions de Dirichlet est un sous-espace vectoriel de l'espace vectoriel des fonctions numériques univariées définies sur ou ; ou celui des fonctions numériques univariées -périodique. Cet ensemble se note par .
La série de Fourier de toute fonction appartenant à l'ensemble qui est de classe par morceaux est, sur , simplement convergente.
On définit sur l'ensemble une forme bilinéaire de la manière suivante :
L'ensemble munie de la forme bilinéaire est un espace pré-hilbertient (complexe)
On désigne par la famille des éléments de l'ensemble de Dirichlet qui sont définis par :
Et on a les deux propriétés suivantes :
- la famille est une famille orthonormale de l'espace ;
- pour tout nombre entier naturel , le coefficient de Fourier d'une fonction de est égal au produit hermitien .
Soit une fonction numérique univariée de dans ou , -périodique, continue sur et de classe par morceaux. Dans ce cas la série de Fourier de la fonction converge normalement, sur , vers .
Si la famille est une famille orthonormale d'un espace pré-hilbertien quelconque alors, pour on a l'inégalité, dite de Bessel, suivante :
En appliquant cette inégalité à l'espace aux cas des deux suites et des coefficient de Fourier de alors les deux séries numériques et sont convergentes.
Lorsque l'espace pré-hilbertien est il existe le théorème mathématicien français Marc-Antoine Parseval des Chênes (1755-1836) qui est plus puissant que l'inégalité de Bessel : ce n'est plus une inégalité mais une égalité.
Pour toute fonction on a l'égalité suivante :
Et :
Remarque :
Soit un nombre réel strictement positif. Dans le cas des fonctions -périodique on a les définitions suivantes des coefficient de Fourier :
On rappelle qu'une fonction numérique univariée définie sur un ensemble est déclarée de période , ou -périodique, si elle vérifie :
Lorsqu'une fonction est périodique, son graphe reproduit de façon répétitive n’importe quelle portion particulière de longueur égale à une période : c'est une propriété d'invariance par translation.
La série de Fourier associée à , c'est-à-dire le développement trigonométrique ou exponentielle est couramment désigné par .
Question 1
Pour bien débuter.
Soit la fonction numérique , -périodique, dont l'image est, sur l'intervalle , donnée par l'expression . Déterminer l'expression de sa série de Fourier.
Correction
La fonction considérer satisfait aux condition de Dirichlet et de fait elle admet un développement en série de Fourier convergent vers la régularisée associée.
Cette fonction est paire. De fait les coefficients trigonométriques sont tous nuls.
On a :
Donc :
De plus, , on a avec une première intégration par parties :
Comme on obtient :
Nous allons maintenant effectuer une seconde intégration par parties :
Soit :
Soit encore :
Avec :
Or la fonction cosinus est paire, donc . D'où :
De plus :
Ainsi :
Puis :
Ceci nous permet d'écrire que :
Soit :
Donc :
Ceci nous permet d'écrire le développement suivant :
Finalement, comme la régularisée est égale à la fonction (de part sa continuité), on obtient :
Pour visualiser la puissance de ce résultats, voici le graphe de la fonction étudiée :
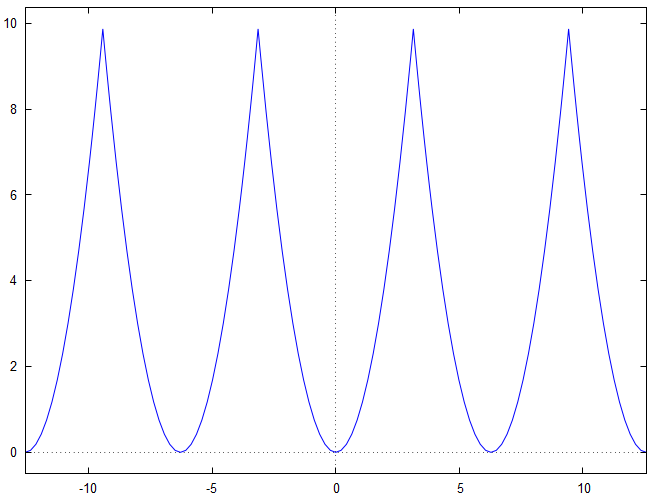
Puis, voici la représentation des graphes de la fonction étudiée et des deux sommes partielles et :
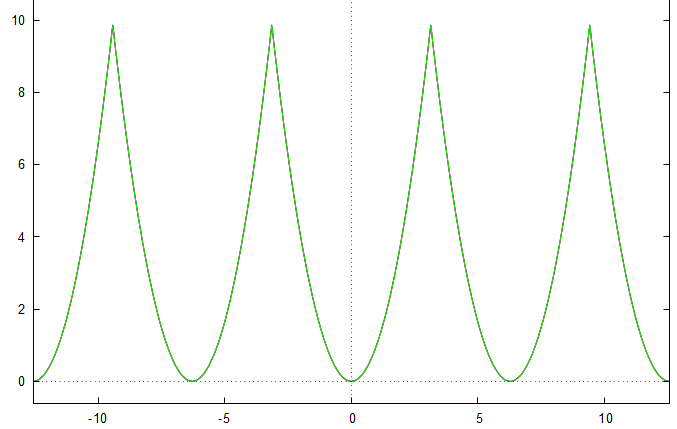
On constate bien que la méthodes des séries de Fourier est très performante.
Cette fonction est paire. De fait les coefficients trigonométriques sont tous nuls.
On a :
Donc :
De plus, , on a avec une première intégration par parties :
Comme on obtient :
Nous allons maintenant effectuer une seconde intégration par parties :
Soit :
Soit encore :
Avec :
Or la fonction cosinus est paire, donc . D'où :
De plus :
Ainsi :
Puis :
Ceci nous permet d'écrire que :
Soit :
Donc :
Ceci nous permet d'écrire le développement suivant :
Finalement, comme la régularisée est égale à la fonction (de part sa continuité), on obtient :
Pour visualiser la puissance de ce résultats, voici le graphe de la fonction étudiée :

Puis, voici la représentation des graphes de la fonction étudiée et des deux sommes partielles et :

On constate bien que la méthodes des séries de Fourier est très performante.
Question 2
En déduire la valeur numérique de la célèbre série numérique de Mengoli, à savoir , ou d'Euler relative au problème de Bâle.
Correction
Nous venons de démontrer que :
Plaçons nous en . On a alors :
On sait que . Donc :
Soit :
Soit encore :
Ceci nous donne donc :
En simplifiant par on obtient :
Donc :
Finalement :
Plaçons nous en . On a alors :
On sait que . Donc :
Soit :
Soit encore :
Ceci nous donne donc :
En simplifiant par on obtient :
Donc :
Finalement :
Question 3
Soit la fonction numérique , -périodique, dont l'image est, sur l'intervalle , donnée par l'expression . Déterminer l'expression de sa série de Fourier.
Correction
la fonction permet d'envisager l'opération de dérivation.
Ainsi, le développement en série de Fourier de sera accessible par la dérivation directe du développement en série de Fourier de l'expression fonctionnelle .
On a alors :
Soit :
Soit encore :
La dérivation s'effectuant par rapport à la variable , nous pouvons écrire que :
Avec et
Ce qui nous donne :
Nous allons donc écrire ceci comme :
En simplifiant par , non nul, on obtient :
Enfin, on sait que . Ce qui finalement nous donne :
La fonction présente, sur , des discontinuités. Il est intéressant d'observer le comportement des sommes partielles au voisinages des discontinuités. La fonction étudiée est le "célèbre signal dents de scie" dont le graphe est le suivant :
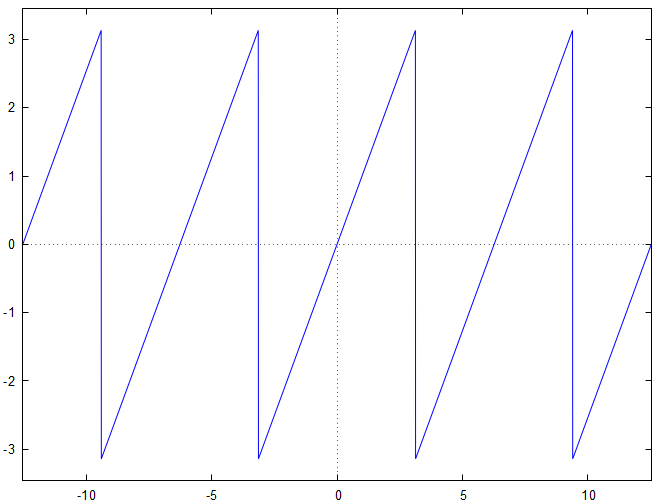
Voici le graphe représentatif de la somme partielle
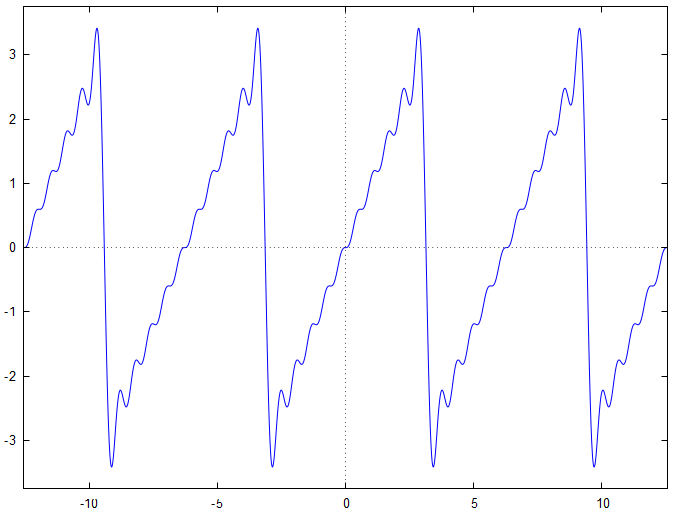
Voici le graphe représentatif de la somme partielle
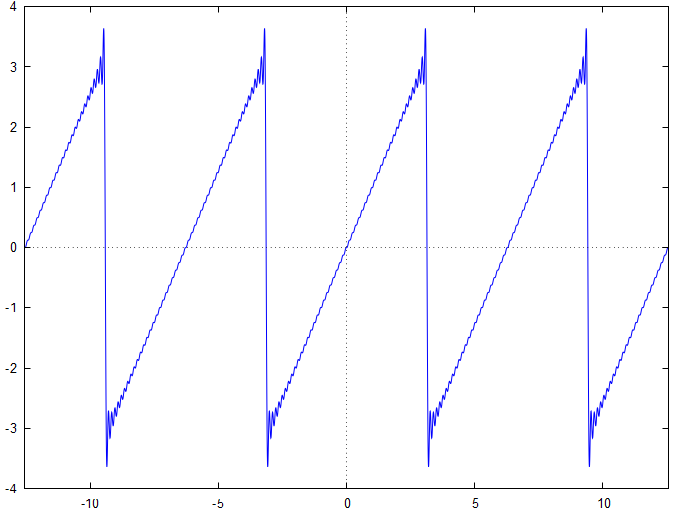
Voici le graphe représentatif de la somme partielle
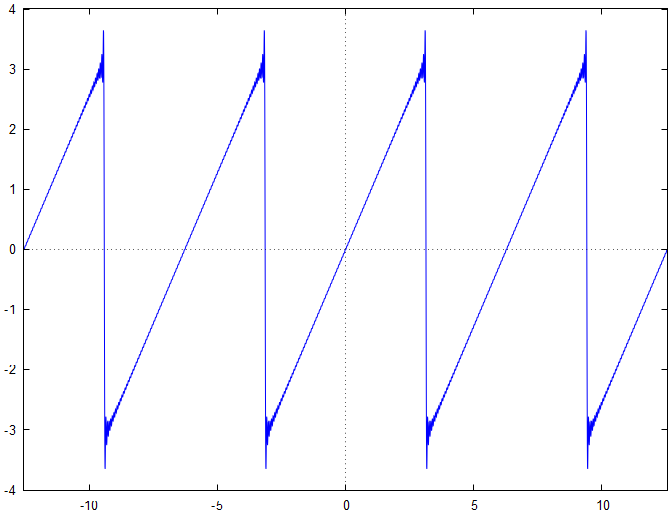
Voici le graphe représentatif de la somme partielle
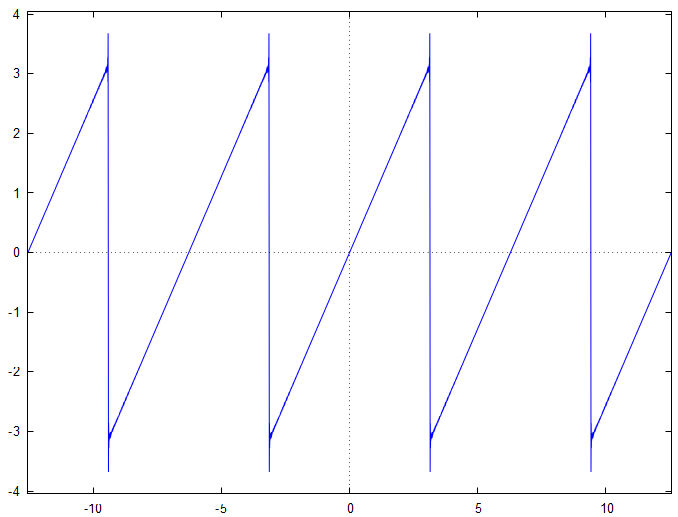
Voici le graphe représentatif de la somme partielle
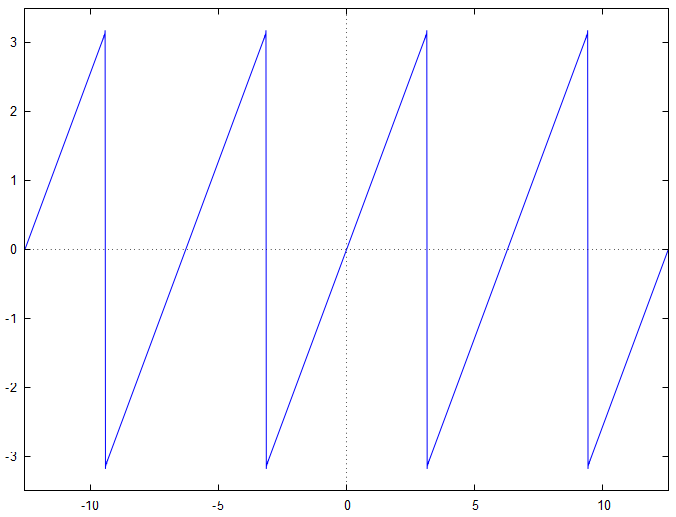
On constate que les comportements particuliers, qui peuvent s'assimiler à une déformation du signal, qui se produisent aux discontinuités se "régularisent" lorsque l'ordre de la somme partielle augmente. Ce comportement est connu sous le nom de phénomène de Gibbs. Ce phénomène est un effet de bord qui se produit à la proximité d'une discontinuité, lors de l'analyse d'une fonction qui est dérivable par morceaux.
Ainsi, le développement en série de Fourier de sera accessible par la dérivation directe du développement en série de Fourier de l'expression fonctionnelle .
On a alors :
Soit :
Soit encore :
La dérivation s'effectuant par rapport à la variable , nous pouvons écrire que :
Avec et
Ce qui nous donne :
Nous allons donc écrire ceci comme :
En simplifiant par , non nul, on obtient :
Enfin, on sait que . Ce qui finalement nous donne :
La fonction présente, sur , des discontinuités. Il est intéressant d'observer le comportement des sommes partielles au voisinages des discontinuités. La fonction étudiée est le "célèbre signal dents de scie" dont le graphe est le suivant :

Voici le graphe représentatif de la somme partielle

Voici le graphe représentatif de la somme partielle

Voici le graphe représentatif de la somme partielle

Voici le graphe représentatif de la somme partielle

Voici le graphe représentatif de la somme partielle

On constate que les comportements particuliers, qui peuvent s'assimiler à une déformation du signal, qui se produisent aux discontinuités se "régularisent" lorsque l'ordre de la somme partielle augmente. Ce comportement est connu sous le nom de phénomène de Gibbs. Ce phénomène est un effet de bord qui se produit à la proximité d'une discontinuité, lors de l'analyse d'une fonction qui est dérivable par morceaux.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.