♣NotionssurlesensemblesOn peut imaginer, de manière un peu naïve,
unensemble comme étant une collection d'objets.
Si on note par
x l'objet qui appartient à l'ensemble
E, on note ceci comme
x∈E, et doit se lire
xappartientaˋE.
Dans le cas où
x n'appartient pas à l'ensemble
E, on note ceci
x∈/E.
Il y a plusieurs manière de décrire un ensemble
E, les deux plus courantes sont les suivantes :
↬EnextensionC'est lorsque l'on précise tous les éléments qui constituent l'ensemble
E. On doit indiquer les différents éléments constitutifs de
E entre deux accolades, et séparés par une virgule ou un point virgule. Par exemple :
E={1;3;5;7;9}.
↬EncompreˊhensionC'est lorsque les éléments constitutifs ne sont pas tous explicitement mentionnés. Cependant, on dispose d'un critère pour savoir si un objet donné appartient ou non dans l'ensemble considéré. Par exemple, on considère l'ensemble
E suivant :
E={n∈N/2n+1estunnombrepremier}, qui se lit comme
"nestunnombreentiernatureltelquelaquantiteˊ2n+1soitunnombrepremier".
Il n'est pas possible d'énumérer tous les éléments de
E. On peut, par exemple dire que
2 est un élément de
E car il correspond au cas
n=0, mais que
7 n'appartient pas à l'ensemble
E.
Un ensemble qui contient uniquement
unseuleˊleˊment est appelé
unsingleton.
On admet l'existence d'un ensemble qui ne contient
aucuneˊleˊment, c'est l'
ensemblevide, et il se note
∅.
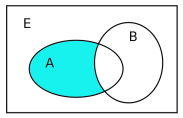
∙InclusionSoit
E et
F deux ensembles. On dit que
F est un sous-ensemble de
E si tout élément de
F est également un élément de
E. On dit alors que
F est inclus dans
E, ou que
F est une partie de
E, et on note ceci comme
E⊂F. A la définition mathématiques
∀x∈A, x∈B on associe la figure :
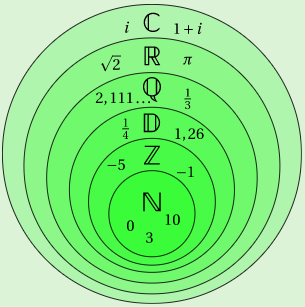
On connait tous la suite d'inclusion suivante :
N⊂Z⊂D⊂Q⊂R⊂C⊂...Bien sur, on a l'inclusion suivante
E⊂E. Et de plus, il est évident que pour les trois ensembles
A,
B et
C, on a la propriété de
transitiviteˊ suivante :
((A⊂B)∧(B⊂C))⟹(A⊂C)Par convention, l'ensemble vide
∅ est inclus dans tous les autres ensembles. Donc
∅ est une partie de
E :
∅⊂E.
L'ensemble qui contient toutes les parties possibles de
E se note
P(E). Cet ensemble
P(E) s'appelle
l′ensembledespartiesdeE. Donc cet ensemble
P(E) n'est jamais vide puisqu'il contient, bien évidemment,
E lui-même et aussi l'ensemble vide
∅.
Par exemple, si
E={a;b} alors
P(E)={∅;{a};{b};E}∙∙EgaliteˊSoit
E et
F deux ensembles. On dit que
E est égal à
F si on a
E⊂F et
F⊂E. Et on note ceci
E=F.
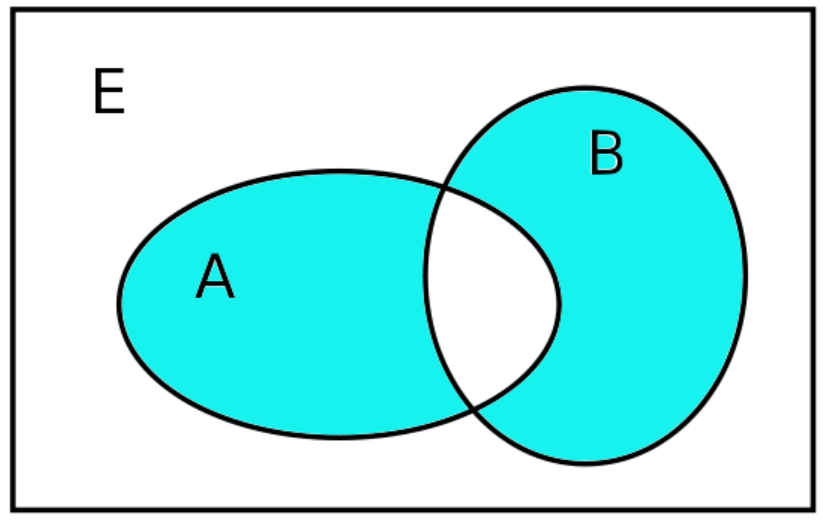
∙∙∙IntersectionSoit
A et
B deux parties de
E. L'
intersection des parties
A et
B est l'ensemble des éléments qui appartiennent
aˋ lafois à
A et à
B. On note cet ensemble intersection par :
A∩B. On peut lire ceci comme
A et B. On a alors la définition mathématique suivante
(x∈(A∩B)⊂E)⟺((x∈A)∧(x∈B)), et l'on associe la figure (de
Venn) :
Et on a les quatre propriétés (évidentes) suivantes :
1−A∩E=A2−A∩∅=∅3−(A∩B)⊂A4−(A∩B)⊂BLorsque deux ensembles
A et
B d'un même ensemble
E vérifient
A∩B=∅, ont dit alors que les deux ensembles
A et
B sont
disjoints.
∙∙∙∙ReˊunionSoit
A et
B deux parties de
E. La
reˊunion des parties
A et
B est l'ensemble des éléments qui appartiennent à
A ou à
B. On note cet ensemble réunion par :
A∪B. On peut lire ceci comme
A ou B. Il s'agit d'un
ouinclusif car l'intersection appartient à la réunion. On a alors la définition mathématique suivante
(x∈(A∪B)⊂E)⟺((x∈A)∨(x∈B)), et l'on associe la figure (de
Venn) :
Et on a les sept propriétés (évidentes) suivantes :
1−A∪E=E2−A∪∅=A3−A⊂(A∪B)4−B⊂(A∪B)5−A=A∪(A∩B)6−B=B∪(A∩B)7−((A∪B)=∅)⟺((A=∅)∧(B=∅))∙∙∙∙∙CompleˊmentaireSoit
A une partie de
E. On définit
lapartiecompleˊmentaire, encore appelé le
compleˊmentaire de
A dans
E, noté
∁EA ou
A, comme étant l'ensemble des éléments de
E quinesontpas dans
A. On a donc la définition mathématique suivante
(x∈∁EA)⟺((x∈E)∧(x∈/A)) et on associe la figure (de
Venn) :
Et on a les cinq propriétés (évidentes) suivantes :
1−A∪∁EA=E2−A∩∁EA=∅3−A=A4−∁EE=∅−∁E∅=EAinsi, si
A et
B sont deux parties de
E alors on dit que
A est le complémentaire de
B sur
E (Et
B est le complémentaire de
A sur
E) lorsque :
(A=∁EB)⟺(((A∪B)=E)∧((A∩B)=∅))Et bien évidemment :
(B=∁EA)⟺(((A∪B)=E)∧((A∩B)=∅))De plus, si
A⊂B alors
∁EB⊂∁EA.
∙∙∙∙∙∙DiffeˊrenceSoit
A et
B deux parties d'un même ensemble
E. La différence de
A avec
B est l'ensemble des éléments de
A qui n'appartiennent pas à
B. On le note
A∖B ou
A−B.
On associe donc la définition mathématique suivante
((x∈(A∖B)⊂E)⟺((x∈A)∧(x∈/B)). A laquelle on associe la figure suivante :
Ce qui entraîne que
A∖B=A∩B.
De plus, si
A⊂B alors
B∖A=∁AB.
Le lien avec la réunion et l'union est donné par la relation importante suivante :
A∪B=(A∖B)∪(A∩B)∪(B∖A)Si
A et
B sont deux parties d'un même ensemble
E alors on a :
E∖A=∁EA.
Sur la figure précédente, on constate que
A=(A∖B)∪(A∩B) et aussi que
B=(A∩B)∪(B∖A).
Enfin, mentionnons la propriété évidente suivante :
(A∖B=∅)⟺(A⊂B)∙∙∙∙∙∙∙DiffeˊrencesymeˊtriqueLa différence symétrique de
A et de
B, est notée «
AΔB » (et doit se lire «
A delta
B ») est l'ensemble des éléments qui appartiennent soit à
A, soit à
B,
maispasaux deuxaˋlafois.
La différence symétrique de
A et de
B est la différence de
A∪B et de
A∩B. On peut l'écrire sous les formes suivantes :
AΔB=(A∪B)∖(A∩B)=(A∖B)∪(B∖A)=(A∩B)∪(B∩A)Autrement dit
x∈(AΔB)⊂E signifie que
x appartient à un, et un seul, des ensembles
A et
B. Il s'agit d'utiliser le
ouexclusif. On a donc la définition
((x∈(AΔB)⊂E)⟺((x∈A)∨exclusif(x∈B)) et que l'on associe à la figure (de
Venn) :
Soit
A,
B et
C trois parties d'un même ensemble
E. On a alors les quatre propriétés suivantes :
1−AΔ∅=A2−AΔA=∅3−AΔB=BΔA (commutativité)
4−AΔ(BΔC)=(AΔB)ΔC (associativité).
∢:RemarqueL'intersection, la réunion et le complémentaire permettent de définir un calcul algébrique dans
P(E). Ce calcul algébrique sur l'ensemble des parties de
E porte le nom
d′algeˋbredeBoole.
♣♣LoissurlesensemblesSoit
A,
B et
C trois parties de l'ensemble
E.
↬IdempotenceOn a :
{A∪AA∩A==AA↬CommutativiteˊOn a :
{A∪BA∩B==B∪AB∩A↬AssociativiteˊOn a :
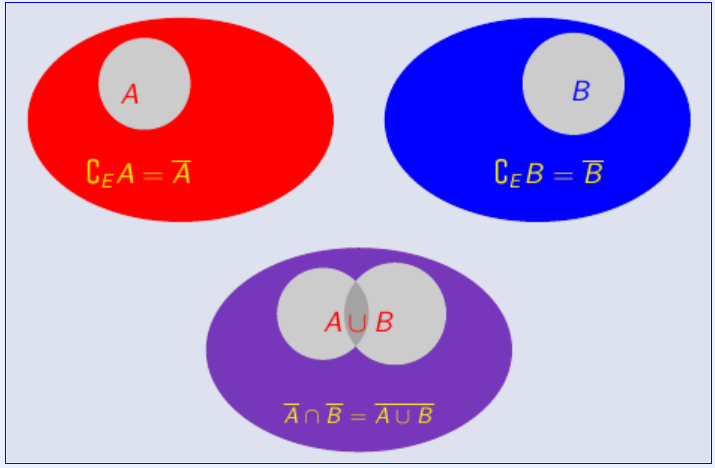
{(A∪B)∪C(A∩B)∩C==A∪(B∪C)A∩(B∩C)↬PremieˋreloideMorganOn a :
A∪B=A∩BQue l'on associe à la figure :
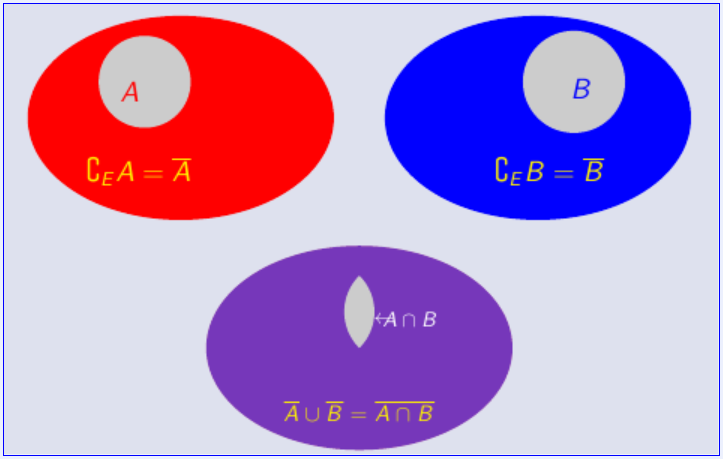
↬SecondeloideMorganOn a :
A∩B=A∪BQue l'on associe à la figure :
♣♣♣EnsemblesusuelsOn désigne généralement les ensembles les plus usuels par une lettre à double barre. On a :
∙N: ensemble des nombres entiers naturels,
∙N⋆: ensemble des nombres entiers naturels strictement positifs,
∙Z: ensemble des nombres entiers relatifs,
∙Z⋆: ensemble des nombres entiers relatifs non nuls,
∙D: ensemble des nombres décimaux
(10pn,n∈Z,p∈N),
∙Q: ensemble des nombres rationnels
(qp,p∈Z,q∈Z⋆),
∙R: ensemble des nombres réels,
∙R⋆: ensemble des nombres réels non nuls,
∙R+: ensemble des nombres réels positifs ou nul,
∙C: ensemble des nombres complexes
(a+ib,(a;b)∈R2,i2=−1),
∙H: ensemble des nombres quaternions,
∙O: ensemble des nombres octonions,
∙S: ensemble des nombres sédénions.
Classiquement, on a les inclusions suivantes :
♣♣♣♣Produitd′ensemblesSoit
A et
B deux ensembles non vides d'éléments génériques respectifs
a et
b. On appelle
produitcarteˊsien de
A et
B, noté
A×B, et que l'on doit lire
A croix
B, l'ensemble de tous les couples (ou duets)
(a;b). On a alors :
A×B={(a;b)/a∈A,b∈B}Soit :
((a;b)∈(A×B))⟺((a∈A)∧(b∈B))Si les deux ensembles
A et
B sont dénombrables, alors on note par
card(A) (qui se lit cardinal de
A) le nombre d'éléments
a qui constituent l'ensemble
A, et par
card(B) (qui se lit cardinal de
B)le nombre d'éléments
b qui constituent l'ensemble
B. Dans ce cas, on a :
card(A×B)=card(A)×card(B).
Et bien évidemment on a
A×∅=∅. Si
A est dénombrable, alors
card(A×∅)=card(∅)=0.
Prenons soins de ne
pasconfondre le couple
(a;b), ou l'ordre a de l'importance, avec l'ensemble
{a;b}, ou l'ordre n'a pas d'importance.
Puis, on peut généraliser. Soit
n en nombre entier naturel supérieur ou égal à deux. On définit le produit cartésien des
n ensembles
E1,E2,⋯,En comme l'ensemble des
n-uplets
(x1,x2,⋯,xn) où chaque
xi est un élément quelconque de
Ei, avec
i={1,2,⋯,n}. On note cet ensemble produit cartésien
E1×E2×⋯×En. Et on a :
E1×E2×⋯×En={(x1,x2,⋯,xn))/∀i∈{1,2,⋯,n},xi∈Ei}Si les
n ensembles sont identiques, alors on note
E1×E2×⋯×En=En.
Si les
n ensembles
Ei, avec
i={1,2,⋯,n}, sont dénombrables, alors on a la relation suivante :
card(E1×E2×⋯×En)=card(E1)×card(E2)×⋯×card(En).
∢:Remarque∙ L'ensemble
i={1,2,⋯,n} peut également s'écrire
i∈[[1;n]].
∙∙ On rappelle que si
A et
B sont deux parties d'un même ensemble
E alors on a :
card(A∪B)=card(A)+card(B)−card(A∩B)∙∙∙ On en déduit également que si
A,
B et
C sont trois parties d'un même ensemble
E alors on a :
card(A∪B∪C)=card(A)+card(B)+card(C)−card(A∩B)−card(A∩C)−card(B∩C)+card(A∩B∩C)∙∙∙∙ Soit
n∈N⋆ parties
E1,E2,⋯,En dénombrables d'un même ensemble
E lui même dénombrable. Si ces
n∈N⋆ parties
E1,E2,⋯,En dénombrables sont
toutesdisjointesdeuxaˋdeux alors :
card(E1∪E2∪⋯∪En)=card(E1)+card(E2)+⋯+card(En)Que l'on peut également écrire de manière plus abrégée comme :
card(i=1⋃nEi)=i=1∑ncard(Ei)