Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Problème - Exercice 1
3 h
240
En physique, un milieu semi-infini est un milieu hypothétique occupant tout un demi-espace, c'est-à-dire s'étendant à l'infini dans les trois directions mais d'un seul côté d'un plan. Dans un repère orthonormé, il est par exemple défini par quelconque, quelconque et (ou ). En général ses propriétés sont supposées ne pas dépendre de et .
L'hypothèse d'un milieu semi-infini est une hypothèse simplificatrice utilisée pour la mise en équation et la simulation numérique de nombreux problèmes physiques. Il s'agit en réalité de faire l'hypothèse que les dimensions du milieu en question sont suffisamment grandes pour que les bords autres que le plan n'aient aucune incidence pratique sur le système.
La face d'un milieu conducteur semi-infini à une dimension, initialement à la température nulle, est portée à une température donnée par . Ce milieu semi-infini est représenté par le schéma suivant :

Les plans sont donc des lieux de points isothermes, dont la température sera notée . Ces dernières sont les solutions d'un problème thermique modélisé par l'équation de la chaleur suivante :
Dans cette relation . Et on associe, à cette équation, les conditions suivantes :
Pour , on adoptera les écritures suivantes :
En outre, pour , on admettra la transformation (issue de l'Analyse Complexe) :
L'hypothèse d'un milieu semi-infini est une hypothèse simplificatrice utilisée pour la mise en équation et la simulation numérique de nombreux problèmes physiques. Il s'agit en réalité de faire l'hypothèse que les dimensions du milieu en question sont suffisamment grandes pour que les bords autres que le plan n'aient aucune incidence pratique sur le système.
La face d'un milieu conducteur semi-infini à une dimension, initialement à la température nulle, est portée à une température donnée par . Ce milieu semi-infini est représenté par le schéma suivant :

Les plans sont donc des lieux de points isothermes, dont la température sera notée . Ces dernières sont les solutions d'un problème thermique modélisé par l'équation de la chaleur suivante :
Dans cette relation . Et on associe, à cette équation, les conditions suivantes :
Pour , on adoptera les écritures suivantes :
En outre, pour , on admettra la transformation (issue de l'Analyse Complexe) :
Question 1
Soient . Démontrer que l'on a la solution mathématique suivante :
Correction
On a l'équation suivante :
Soit :
D'où :
Or, par hypothèse, on sait que , ce qui nous permet d'écrire :
L'équation caractéristique s'écrit :
Ainsi, avec , on a la solution mathématique suivante :
Soit :
D'où :
Or, par hypothèse, on sait que , ce qui nous permet d'écrire :
L'équation caractéristique s'écrit :
Ainsi, avec , on a la solution mathématique suivante :
Question 2
Montrer que, pour être physiquement acceptable, la solution précédente doit prendre la forme suivante :
Correction
Lorsque , on a .
Cependant cela n'est physiquement pas possible car les quantités physiques doivent rester bornées. Ceci impose nécessairement que . La solution précédente est alors de la forme suivante :
Cette solution doit être vérifiée pour toute valeur de , et donc pour également. On a alors :
Or, si , on doit également avoir :
Ce qui implique que :
Ce qui nous permet de conclure que la solution, physiquement acceptable, est donnée par :
Cependant cela n'est physiquement pas possible car les quantités physiques doivent rester bornées. Ceci impose nécessairement que . La solution précédente est alors de la forme suivante :
Cette solution doit être vérifiée pour toute valeur de , et donc pour également. On a alors :
Or, si , on doit également avoir :
Ce qui implique que :
Ce qui nous permet de conclure que la solution, physiquement acceptable, est donnée par :
Question 3
Le milieu semi-infini est un filtre linéaire dont la température interne est la réponse à l'excitation . Sa est . Démontrer alors que :
Correction
On a :
Ce qui nous permet d'écrire que :
Soit encore :
En sortant le terme constant , vis-à-vis de la variable , on obtient :
Cependant, le phénomène étudié se produit sur la plage temporelle , avec pour le physicien. C'est pourquoi on peut écrire que :
Ce qui nous permet d'écrire que :
Soit encore :
En sortant le terme constant , vis-à-vis de la variable , on obtient :
Cependant, le phénomène étudié se produit sur la plage temporelle , avec pour le physicien. C'est pourquoi on peut écrire que :
Question 4
Par un changement de variable adéquat que vous préciserez (vous exprimerez clairement mais également les bornes associées à ), montrer que :
Correction
Effectuons le changement de variable suivant :
En ce qui concerne les bornes d'intégration, lorsque on a et la borne correspondante à devient . On a alors :
On en déduit alors que :
On va donc pouvoir écrire que :
En simplifiant et en renversant l'ordre des bornes d'intégration, on obtient bien :
En ce qui concerne les bornes d'intégration, lorsque on a et la borne correspondante à devient . On a alors :
On en déduit alors que :
On va donc pouvoir écrire que :
En simplifiant et en renversant l'ordre des bornes d'intégration, on obtient bien :
Question 5
On pose dans cette \textsc{Partie} 2 que :
Ce type de fonction permet de modéliser simplement la pénétration, sur différentes échelles de temps, des ondes thermiques dans les sols.
On notera par le nombre complexe imaginaire, tel que .
On rappelle que, si tel que , alors on a la relation suivante :
On rappelle également que, , l'intégrale de la partie réelle de est égale à la partie réelle de l'intégrale de :
Démontrer que :
Correction
On a :
Soit encore :
Ce que nous pouvons encore écrire, vis-à-vis des bornes d'intégration, comme :
Soit encore :
Ce qui vas encore s'écrire sous la forme :
Soit encore :
Ce que nous pouvons encore écrire, vis-à-vis des bornes d'intégration, comme :
Soit encore :
Ce qui vas encore s'écrire sous la forme :
Question 6
Montrer que :
Correction
Pour chaque valeur de , le terme est majoré par :
Ainsi, on a :
De plus, on a :
Donc, on peut écrire que :
Ce qui nous permet d'écrire que :
Finalement, on en déduit que :
Ainsi, on a :
De plus, on a :
Donc, on peut écrire que :
Ce qui nous permet d'écrire que :
Finalement, on en déduit que :
Question 7
Pour des temps suffisamment grands vis-à-vis d'un temps caractéristique du processus de propagation, (qui représente un état thermique transitoire). Sous cette hypothèse, démontrer que :
Où est un nombre complexe dont vous préciserez l'expression.
Où est un nombre complexe dont vous préciserez l'expression.
Correction
Soit l'hypothèse proposée, on a alors :
Soit :
Soit encore :
Ainsi, on obtient :
On peut donc écrire ceci comme :
Mais, l'exponentielle présente dans cette intégrale peut également s'écrire comme :
Posons maintenant :
Ainsi, on obtient :
Ou encore en faisant usage d'une identité remarquable pour factoriser :
Puis, on a :
Ce qui nous permet d'écrire que :
Ce qui nous permet d'écrire que :
La température recherchée prend alors la forme suivante :
En sortant de l'intégrale le terme , on trouve que :
Soit :
Soit encore :
Ainsi, on obtient :
On peut donc écrire ceci comme :
Mais, l'exponentielle présente dans cette intégrale peut également s'écrire comme :
Posons maintenant :
Ainsi, on obtient :
Ou encore en faisant usage d'une identité remarquable pour factoriser :
Puis, on a :
Ce qui nous permet d'écrire que :
Ce qui nous permet d'écrire que :
La température recherchée prend alors la forme suivante :
En sortant de l'intégrale le terme , on trouve que :
Question 8
Démontrer, sous l'hypothèse des temps suffisamment longs, que la température dans le milieux semi-infini est donnée, par l'expression suivante :
Correction
On a :
D'après le sujet, on sait que , ce qui nous permet d'écrire que :
Soit :
Ou encore :
En associant les deux exponentielles complexes entre-elles, on trouve que :
En factorisant par dans l'exponentielle complexe, on obtient :
Or, , on a . Ainsi, on trouve finalement que :
D'après le sujet, on sait que , ce qui nous permet d'écrire que :
Soit :
Ou encore :
En associant les deux exponentielles complexes entre-elles, on trouve que :
En factorisant par dans l'exponentielle complexe, on obtient :
Or, , on a . Ainsi, on trouve finalement que :
Question 9
En déduire une distance caractéristique, notée , de ce phénomène de propagation d'ondes thermiques.
Correction
Le terme est sans dimension, ce qui implique nécessairement que son argument l'est aussi. Donc le terme est aussi sans dimension. Comme est une longueur alors représente l'inverse d'une longueur. C'est donc l'inverse d'une distance caractéristique du phénomène de propagation thermique. On a alors :
.
.
Question 10
En déduire un temps caractéristique, noté , de ce phénomène de propagation d'ondes thermiques.
Correction
De la même manière, le terme est sans dimension. Ce qui signifie que à les dimensions de l'inverse d'un temps. Ainsi son inverse représente un temps caractéristique du phénomène de propagation thermique. On a alors :
Ce qui implique que :
Ce qui implique que :
Question 11
En déduire une vitesse caractéristique, notée , de ce phénomène de propagation d'ondes thermiques.
Correction
Pour déduire une vitesse caractéristique, notée , de ce phénomène, on écrit simplement que :
Finalement, on trouve que :
Remarque :
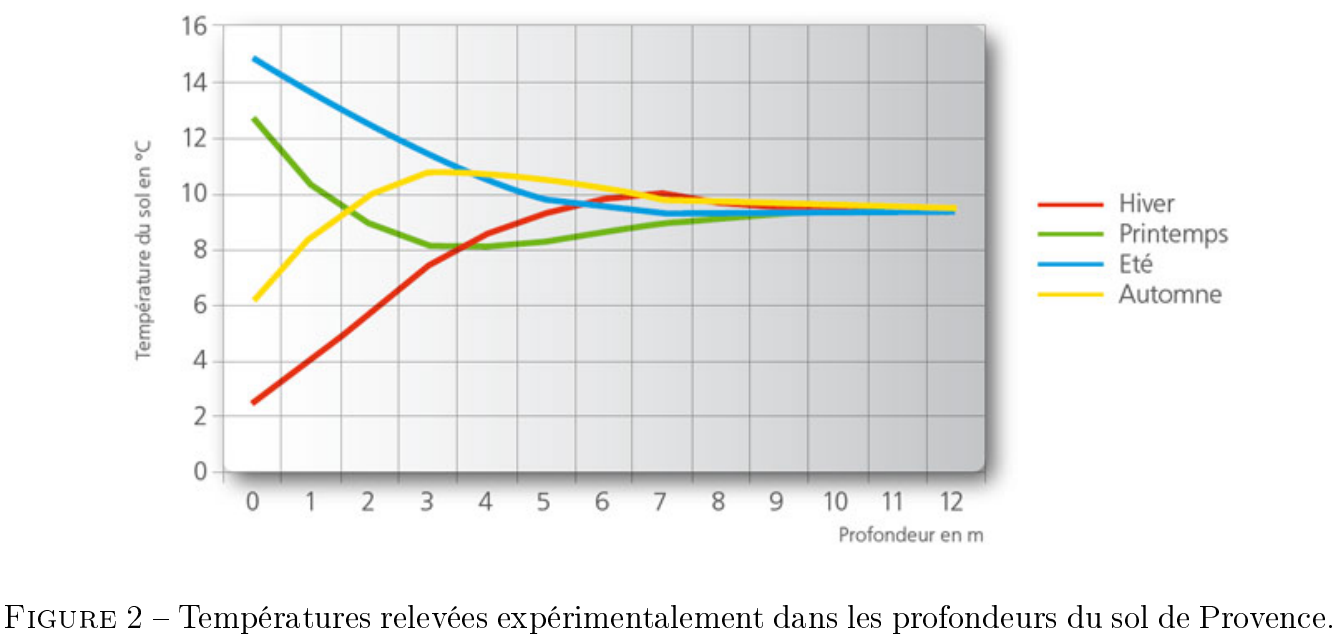
La température de l'air extérieur dans la plupart des pays européens peut varier de à tout au long de l'année, alors que la température du sol à quelques mètres de profondeur reste plus stable, entre et en moyenne. Les solutions trouvées dans cet exercice permette de modéliser ce phénomène. L'accord entre les relevés de température en profondeur à différentes périodes de l'année sont en parfait accord avec les prédictions théoriques. Ceci nous permet d'obtenir :
Finalement, on trouve que :
Remarque :
La température de l'air extérieur dans la plupart des pays européens peut varier de à tout au long de l'année, alors que la température du sol à quelques mètres de profondeur reste plus stable, entre et en moyenne. Les solutions trouvées dans cet exercice permette de modéliser ce phénomène. L'accord entre les relevés de température en profondeur à différentes périodes de l'année sont en parfait accord avec les prédictions théoriques. Ceci nous permet d'obtenir :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.