Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 4 - Exercice 1
30 min
45
Un exemple plus délicat.
Question 1
Soit une fonction univariée et causale qui doit satisfaire aux deux conditions initiales suivantes : et .
En outre, cette fonction numérique vérifie l'équation différentielle ordinaire (EDO) suivante : .
En outre, cette fonction numérique vérifie l'équation différentielle ordinaire (EDO) suivante : .
Déterminer l'expression de la fonction causale qui satisfait aux conditions exposées ci-avant.
Correction
Comme on recherche une fonction causale, introduisons l'échelon unité dans l'équation différentielle proposée ci-avant :
Prenons maintenant la transformée de Laplace de chaque membre de cette équation. On a alors :
Par linéarité de la transformée de Laplace, on obtient alors :
On va adopter la notation usuelle , avec . D'après les propriétés de la transformée de Laplace, on a alors :
En faisant usage des conditions initiales, on a alors :
Soit :
Soit :
En isolant , on obtient :
Or, le polynôme du second degré, en , admet deux racines réelles distinctes qui sont et (le discriminant associé étant ). Donc on a la factorisation suivante :
Ainsi :
De plus, on a :
Le polynôme du second degré n'admet pas de racine réelle. Donc nous allons le laisser sous sa forme développée. On a alors :
En décomposant en élément simples, on peut écrire, avec les trois nombres réels , et , que :
En posant , on trouve que :
Donc :
Puis, on a :
Posons alors , dans ce cas on a :
On peut également écrire que :
Posons maintenant . On a alors :
De fait, on a immédiatement :
De fait, on obtient :
Ain, on obtient :
Mais, on sait que , ceci nous permet d'écrire que :
Donc, on a également :
Soit :
Par linéarité de la transformation de Laplace, on a :
Afin de satisfaire à la condition de causalité, introduisons l'échelon unité :
Graphiquement, on observe que :
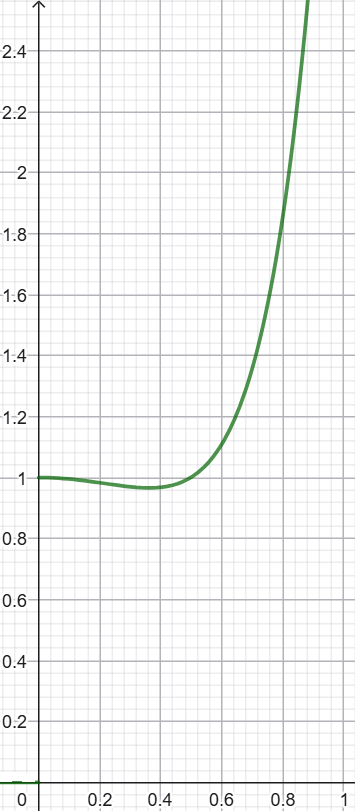
Prenons maintenant la transformée de Laplace de chaque membre de cette équation. On a alors :
Par linéarité de la transformée de Laplace, on obtient alors :
On va adopter la notation usuelle , avec . D'après les propriétés de la transformée de Laplace, on a alors :
En faisant usage des conditions initiales, on a alors :
Soit :
Soit :
En isolant , on obtient :
Or, le polynôme du second degré, en , admet deux racines réelles distinctes qui sont et (le discriminant associé étant ). Donc on a la factorisation suivante :
Ainsi :
De plus, on a :
Le polynôme du second degré n'admet pas de racine réelle. Donc nous allons le laisser sous sa forme développée. On a alors :
En décomposant en élément simples, on peut écrire, avec les trois nombres réels , et , que :
En posant , on trouve que :
Donc :
Puis, on a :
Posons alors , dans ce cas on a :
On peut également écrire que :
Posons maintenant . On a alors :
De fait, on a immédiatement :
De fait, on obtient :
Ain, on obtient :
Mais, on sait que , ceci nous permet d'écrire que :
Donc, on a également :
Soit :
Par linéarité de la transformation de Laplace, on a :
Afin de satisfaire à la condition de causalité, introduisons l'échelon unité :
Graphiquement, on observe que :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.