Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 3 - Exercice 1
20 min
30
On continu sur des exemples élémentaires pour apprendre les réflexes fondamentaux.
Question 1
On considère une fonction univariée et causale telle que . En outre cette fonction satisfait à l'équation différentielle ordinaire (EDO) suivante :
Déterminer l'expression de la fonction causale qui satisfait aux conditions énoncées ci-avant.
Correction
Comme on recherche une fonction causale, introduisons l'échelon unité dans l'équation différentielle proposée :
Prenons maintenant la transformée de Laplace de chaque membre de cette équation. On a alors :
Par linéarité de la transformée de Laplace, on obtient alors :
On va adopter la notation usuelle , avec . D'après les propriétés de la transformée de Laplace, on a alors :
En faisant usage de la condition initiale, on a alors :
Soit :
En isolant , on obtient :
Soit :
Ainsi :
En réduisant au même dénominateur :
Puis sous une fraction uique :
En simplifiant :
En décomposant en élément simples, on peut écrire que :
Dans cette dernière relation, les deux quantités et sont deux nombres réels. Si on pose alors on obtient :
Donc :
Soit :
Soit encore :
Par identification on a immédiatement et de fait . On a alors . On peut alors écrire que :
Ceci peut également s'écrire comme :
Par linéarité, on a :
D'où :
mais, on sait que :
Ce qui nous donne :
Nous allons introduire l'échelon unité afin de s'assurer d'une réponse recherchée qui soit bien causale. Donc on a également:
Finalement, on trouve que :
On peut vérifier graphiquement que la condition initiale imposée est bien satisfaite :
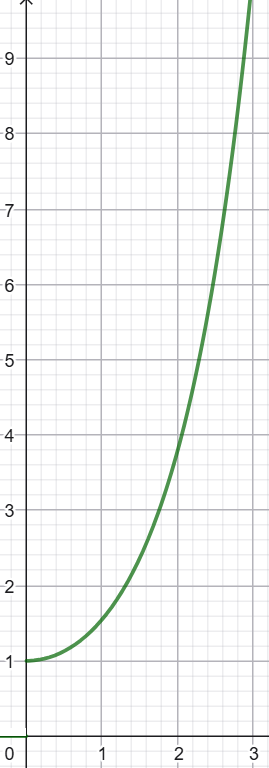
Prenons maintenant la transformée de Laplace de chaque membre de cette équation. On a alors :
Par linéarité de la transformée de Laplace, on obtient alors :
On va adopter la notation usuelle , avec . D'après les propriétés de la transformée de Laplace, on a alors :
En faisant usage de la condition initiale, on a alors :
Soit :
En isolant , on obtient :
Soit :
Ainsi :
En réduisant au même dénominateur :
Puis sous une fraction uique :
En simplifiant :
En décomposant en élément simples, on peut écrire que :
Dans cette dernière relation, les deux quantités et sont deux nombres réels. Si on pose alors on obtient :
Donc :
Soit :
Soit encore :
Par identification on a immédiatement et de fait . On a alors . On peut alors écrire que :
Ceci peut également s'écrire comme :
Par linéarité, on a :
D'où :
mais, on sait que :
Ce qui nous donne :
Nous allons introduire l'échelon unité afin de s'assurer d'une réponse recherchée qui soit bien causale. Donc on a également:
Finalement, on trouve que :
On peut vérifier graphiquement que la condition initiale imposée est bien satisfaite :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.