Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 19 - Exercice 1
15 min
20
Il est important de savoir des liens avec les approches graphiques.
Question 1
On considère le graphe suivant :
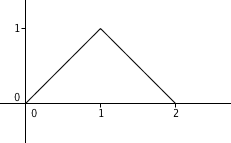

Déterminer, en faisant usage de l'échelon unité, de l'expression de l'image de la fonction correspondante.
Correction
La première des chose est de construire la droite croissante, support du premier segment. L'aspect causal va nous obliger à faire usage de l'échelon unité. Cette droite est donnée par le terme . On a alors :
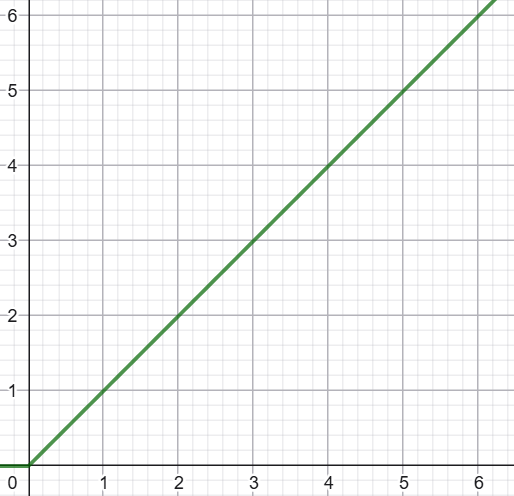
Puis, il nous faut éliminer la partie croissante qui correspond à des abscisses . Pour annuler cette partie, nous allons introduire, au travers d'une addition, à partir de , par l'usage de l'échelon , la droite ; soit le terme . On a alors :
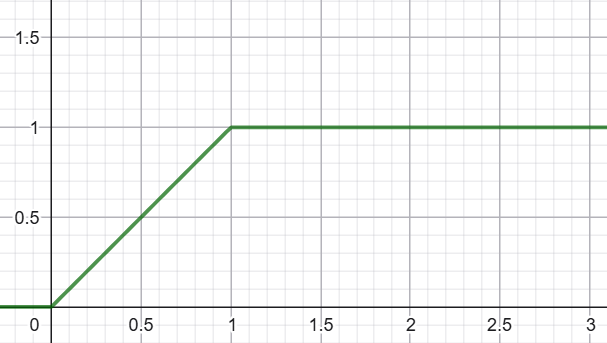
Nous allons construire maintenant le segment qui existe entre les abscisses et . Pour cela, nous allons commencer par ajouter la droite, au travers d'une addition, à partir de , par l'usage de l'échelon , à nouveau la droite ; soit le terme . Ainsi à l'issue du premier segment, qui se trouve entre les abscisses et , vient s'ajouter une demi-droite décroissante. On a alors :
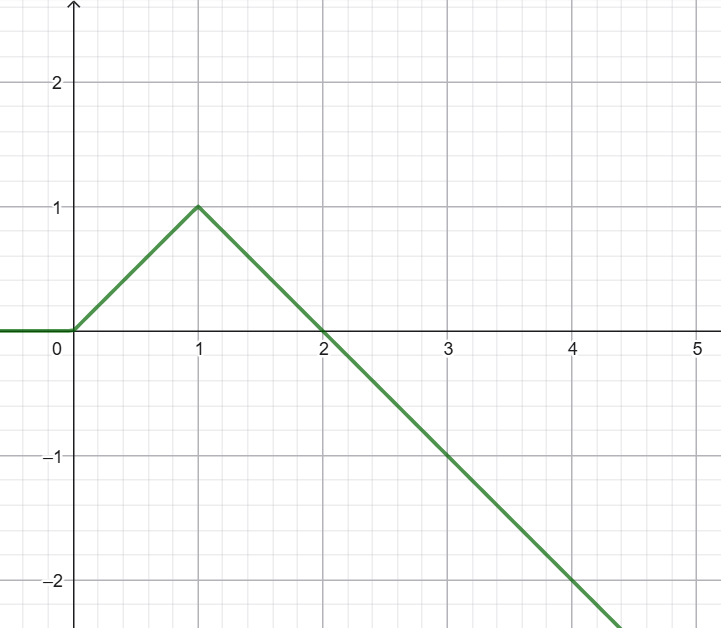
Il nous faut maintenant annuler la partie de cette dernière droite qui se trouve à des abscisses . Pour cela nous allons faire usage de l'échelon qui va agir sur la droite d'équation . On a alors :
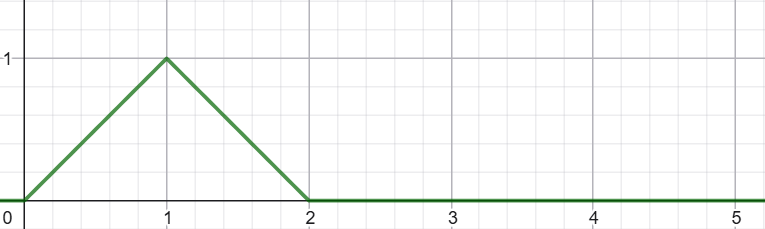
En respectant le schéma constructif précédemment décrit et explicité, on a alors l'expression suivante :
Finalement, on obtient donc :

Puis, il nous faut éliminer la partie croissante qui correspond à des abscisses . Pour annuler cette partie, nous allons introduire, au travers d'une addition, à partir de , par l'usage de l'échelon , la droite ; soit le terme . On a alors :

Nous allons construire maintenant le segment qui existe entre les abscisses et . Pour cela, nous allons commencer par ajouter la droite, au travers d'une addition, à partir de , par l'usage de l'échelon , à nouveau la droite ; soit le terme . Ainsi à l'issue du premier segment, qui se trouve entre les abscisses et , vient s'ajouter une demi-droite décroissante. On a alors :

Il nous faut maintenant annuler la partie de cette dernière droite qui se trouve à des abscisses . Pour cela nous allons faire usage de l'échelon qui va agir sur la droite d'équation . On a alors :

En respectant le schéma constructif précédemment décrit et explicité, on a alors l'expression suivante :
Finalement, on obtient donc :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.