Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 18 - Exercice 1
2 h 30 min
200
En Physique, on rencontre dans de nombreuses branches constitutives (Mécanique, électronique, électricité ...) des comportements oscillatoires caractérisés par l'équation différentielle ordinaire, notée , suivante :
Dans cette équation, le terme est un nombre réel strictement positif qui représente un du phénomène étudié.
Le terme est un nombre réel strictement positif qui caractérise l'oscillation propre du système étudié.
Pour des besoins de réalité physique, on supposera que nous ayons la condition suivante qui est toujours satisfaite :
Le terme est une "fonction " temporelle qui modélise qui entretient l'oscillation du système physique étudié.
Dans notre problème, la variable d'évolution est le temps, noté , et qui satisfait à : .
Les conditions initiales associées à l'équation différentielle (et qui forme le problème de ) seront les suivantes :
On notera par la transformée de de :
Puis, On notera par la transformée de \textit{Laplace} de :
On adoptera la notation :
Pour l'ensemble de ce problème, au besoin, on fera usage des la tables de correspondances du cours relatives à la transformée de .
Question 1
Soit un nombre réel. Déterminer, dans , les racines du polynômes définit par :
Correction
Soit le polynômes définit par :
Le discriminant est donné par l'expression suivante :
Or, on a la condition suivante :
Soit encore :
On pose . Donc, les racines de sont deux nombres complexes conjugués l'un de l'autre, notés et , et qui sont données par :
Soit encore :
Finalement, avec la notation indiquée dans le sujet, on obtient :
Le discriminant est donné par l'expression suivante :
Or, on a la condition suivante :
Soit encore :
On pose . Donc, les racines de sont deux nombres complexes conjugués l'un de l'autre, notés et , et qui sont données par :
Soit encore :
Finalement, avec la notation indiquée dans le sujet, on obtient :
Question 2
Démontrer que :
Correction
On a :
Soit :
Soit encore :
En simplifiant :
Finalement, on a bien démontrer que :
Soit :
Soit encore :
En simplifiant :
Finalement, on a bien démontrer que :
Question 3
Soient et deux nombres réels. On pose :
Démontrer que :
Démontrer que :
Correction
Soient et deux nombres réels. On pose :
On a alors :
Soit :
En observant la table des transformations de donnée dans le cours, on va écrire que :
Ce qui nous donne également :
Soit encore :
Mais aussi :
Ce qui peut également se factoriser comme :
A l'aide de la table des transformations de , on a :
Soit encore :
Ce qui nous donne :
Finalement, on a donc bien démontrer que :
On a alors :
Soit :
En observant la table des transformations de donnée dans le cours, on va écrire que :
Ce qui nous donne également :
Soit encore :
Mais aussi :
Ce qui peut également se factoriser comme :
A l'aide de la table des transformations de , on a :
Soit encore :
Ce qui nous donne :
Finalement, on a donc bien démontrer que :
Question 4
l'expression .
Correction
On a l'expression suivante :
Après une simplification évidente :
Après une simplification évidente :
Question 5
On envisage maintenant l'expression suivante :
Soient les trois nombres réels , et . Déterminer les expressions des trois réels , et qui vérifient :
Soient les trois nombres réels , et . Déterminer les expressions des trois réels , et qui vérifient :
Correction
Soient les trois nombres réels , et . Déterminer les expressions des trois réels , et qui vérifient :
Soit encore :
Ce qui nous donne donc :
On en déduit immédiatement que :
Ce qui nous donne alors :
En développant :
Et de même :
Ce qui nous donne le système suivant :
On a alors :
Soit encore :
Ce qui nous donne donc :
On en déduit immédiatement que :
Ce qui nous donne alors :
En développant :
Et de même :
Ce qui nous donne le système suivant :
On a alors :
Question 6
En déduire que :
Correction
On a donc :
Soit encore :
Ou de même :
En utilisant le résultat de la question 3. avec et , on obtient :
Soit encore :
De manière équivalente, on obtient :
Puis, à l'aide de la table des transformations de , on a . Donc :
Par linéarité de la transformée de , on trouve que :
Dès lors, on constate que l'on a donc bien démontré la relation souhaitée, à savoir :
Soit encore :
Ou de même :
En utilisant le résultat de la question 3. avec et , on obtient :
Soit encore :
De manière équivalente, on obtient :
Puis, à l'aide de la table des transformations de , on a . Donc :
Par linéarité de la transformée de , on trouve que :
Dès lors, on constate que l'on a donc bien démontré la relation souhaitée, à savoir :
Question 7
Dans cette deuxième partie, on considère que l'excitation est en fait une percussion. Il s'agit d'.
Sa durée d'action est infiniment courte et peut-être considérée comme tendant vers zéro. C'est là même le principe de la percussion. Ce type d'excitation peut-être imagée par "un coup de marteau" excitant .
La percussion n'est pas une modélisation académique classique car elle fait appelle à la distribution de . Les distributions, ou fonctions généralisées, étant des outils descriptifs plus avancés dans les concepts mathématiques, leur usage à ce niveau est assez réduit.
En ce sens, avec , on pose :
Représenter graphiquement la distribution de .
Correction
La distribution de , aussi appelée par abus de langage fonction de (ou encore pic de ou même impulsion de ), introduite par le physicien théoricien britannique Paul (1902 - 1984), peut être maladroitement considérée comme une fonction qui prend une "valeur" infinie en , et la valeur zéro partout ailleurs, et dont l'intégrale sur est égale à .
La distribution de est très utile comme approximation de fonctions dont la représentation graphique a la forme d'une grande pointe étroite. C'est le même type d'abstraction qui représente une charge ponctuelle, une masse ponctuelle ou un électron ponctuel. Par exemple, pour calculer la vitesse d'une balle de tennis, frappée par une raquette, nous pouvons assimiler la force de la raquette frappant la balle à une distribution de . De cette manière, nous simplifions non seulement les équations, mais nous pouvons également calculer le mouvement de la balle en considérant seulement toute l'impulsion de la raquette contre la balle, plutôt que d'exiger la connaissance des détails de la façon dont la raquette a transféré l'énergie à la balle.
Par extension, l'expression "un \textit{Dirac}" est donc souvent utilisée par les physiciens pour désigner une fonction ou une courbe "piquée" en une valeur donnée.
Sa représentation graphique est la suivante :
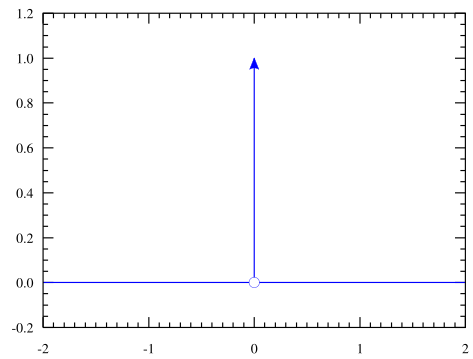
La distribution de est très utile comme approximation de fonctions dont la représentation graphique a la forme d'une grande pointe étroite. C'est le même type d'abstraction qui représente une charge ponctuelle, une masse ponctuelle ou un électron ponctuel. Par exemple, pour calculer la vitesse d'une balle de tennis, frappée par une raquette, nous pouvons assimiler la force de la raquette frappant la balle à une distribution de . De cette manière, nous simplifions non seulement les équations, mais nous pouvons également calculer le mouvement de la balle en considérant seulement toute l'impulsion de la raquette contre la balle, plutôt que d'exiger la connaissance des détails de la façon dont la raquette a transféré l'énergie à la balle.
Par extension, l'expression "un \textit{Dirac}" est donc souvent utilisée par les physiciens pour désigner une fonction ou une courbe "piquée" en une valeur donnée.
Sa représentation graphique est la suivante :

Question 8
Rappeler l'image de la distribution de par transformée de .
Correction
L'image de la distribution de \textit{Dirac} par la transformée de \textit{Laplace} est donnée par :
Question 9
Déterminer l'image associée à cette situation.
Correction
On a l'équation différentielle suivante :
En prenant la transformée de \textit{Laplace} de chaque terme, on obtient :
En tenant compte des conditions initiales, on trouve que :
A savoir :
Donc, on obtient :
Finalement, l'image associée à cette situation est :
En prenant la transformée de \textit{Laplace} de chaque terme, on obtient :
En tenant compte des conditions initiales, on trouve que :
A savoir :
Donc, on obtient :
Finalement, l'image associée à cette situation est :
Question 10
En déduire la solution recherchée .
Correction
En faisant usage de la question 3. de la et en posant et , on trouve que :
Ce qui nous donne :
Finalement, on trouve que la solution recherchée est donnée par l'expression :
Ce qui nous donne :
Finalement, on trouve que la solution recherchée est donnée par l'expression :
Question 11
En terme d'application concrète à ce modèle de percussion, on prend les valeurs numériques suivantes qui respectent les conditions initialement indiquées :
On vous propose les deux représentations graphiques suivantes, l'une en bleue et l'autre, en rouge, . Chacune d'elle a un sens physique et permet de satisfaire à notre modélisation d'un comportement post-percussion. On vous propose les deux représentations graphiques suivantes :
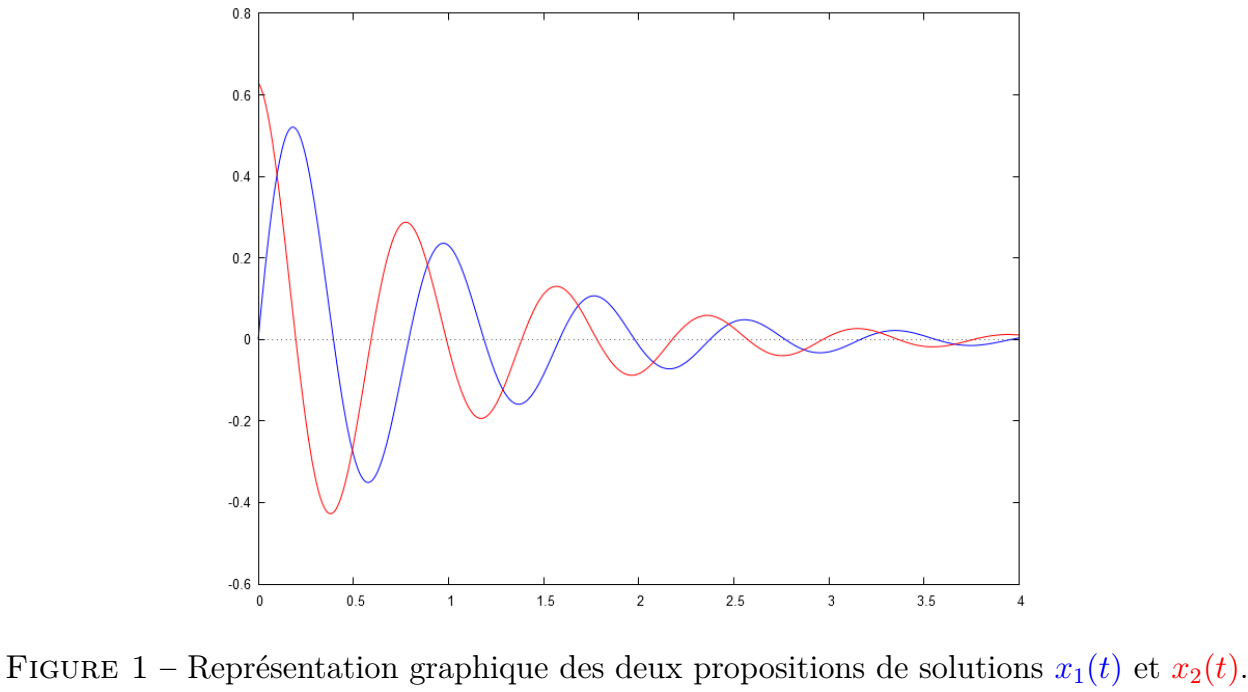
Parmi les deux courbes représentées ci-dessous, laquelle correspond à la solution recherchée dans ce modèle de de percussion ?
On vous propose les deux représentations graphiques suivantes, l'une en bleue et l'autre, en rouge, . Chacune d'elle a un sens physique et permet de satisfaire à notre modélisation d'un comportement post-percussion. On vous propose les deux représentations graphiques suivantes :

Parmi les deux courbes représentées ci-dessous, laquelle correspond à la solution recherchée dans ce modèle de de percussion ?
Correction
Parmi les deux courbes représentées ci-dessous, c'est celle en bleue qui correspond à la solution recherchée dans ce modèle de de percussion. En effet, c'est la seule qui débute à l'origine et définissant le problème de étudié.
Question 12
Dans cette troisième partie, on considère que l'excitation est constante (on dit aussi stationnaire). Ce type d'excitation peut-être imagée par "une pression uniforme" excitante dès .
En ce sens, avec , on pose :
Quelle est l'image, par transformée de Laplace, de l'original ?
Correction
L'image, par transformée de Laplace, de l'original est :
Soit :
Soit :
Question 13
Déterminer l'image associée à cette situation.
Correction
On a l'équation différentielle suivante :
En prenant la transformée de de chaque terme, on obtient :
En tenant compte des conditions initiales, on trouve que :
A savoir :
Donc, on obtient :
Finalement, l'image associée à cette situation est :
En prenant la transformée de de chaque terme, on obtient :
En tenant compte des conditions initiales, on trouve que :
A savoir :
Donc, on obtient :
Finalement, l'image associée à cette situation est :
Question 14
En déduire la solution recherchée .
Correction
On a :
En faisant usage de la question de la question 6. de la on trouve que :
Soit encore :
D'où :
Finalement, on en déduit immédiatement que :
En faisant usage de la question de la question 6. de la on trouve que :
Soit encore :
D'où :
Finalement, on en déduit immédiatement que :
Question 15
En terme d'application concrète à ce modèle d'excitation constante, on prend les valeurs numériques suivantes qui respectent les conditions initialement indiquées :
;
;
;
.
On vous propose les deux représentations graphiques suivantes, l'une en bleue et l'autre, en rouge, . Chacune d'elle a un sens physique et permet de satisfaire à notre modélisation d'un comportement à excitation constante. On vous propose les deux représentations graphiques suivantes :
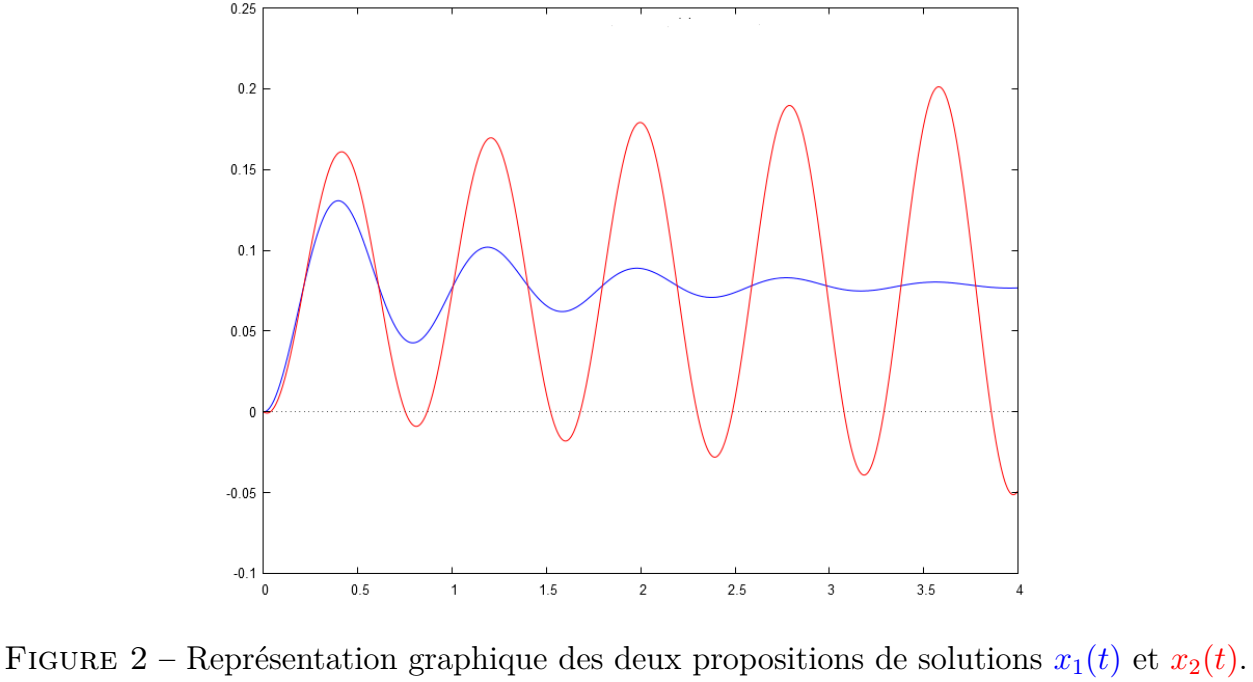
Parmi les deux courbes représentées ci-dessous, laquelle correspond à la solution recherchée dans ce modèle de d'excitation stationnaire ?
;
;
;
.
On vous propose les deux représentations graphiques suivantes, l'une en bleue et l'autre, en rouge, . Chacune d'elle a un sens physique et permet de satisfaire à notre modélisation d'un comportement à excitation constante. On vous propose les deux représentations graphiques suivantes :

Parmi les deux courbes représentées ci-dessous, laquelle correspond à la solution recherchée dans ce modèle de d'excitation stationnaire ?
Correction
Parmi les deux courbes représentées ci-dessous, c'est celle en bleue qui correspond à la solution recherchée dans ce modèle de d'excitation stationnaire. En effet, c'est la seule qui présente définissant le problème de étudié.
Question 16
Dans cette quatrième partie, on considère que l' est quelconque (on dit aussi générale). Ce type d'excitation sera modélisée par . Cette excitation sera notée par comme indiqué initialement dans la section .
A l'aide des tables de correspondances des transformées de , déterminer l'original du terme suivant :
Correction
A l'aide de la table de correspondances des transformées de , on a :
D'après la table des transformées de \textit{Laplace} du sujet, on a :
Finalement :
D'après la table des transformées de \textit{Laplace} du sujet, on a :
Finalement :
Question 17
Soient et deux fonctions causales. Leurs transformées de respectives sont notées et . Exprimer l'original, noté , tel que :
Correction
Soient et deux fonctions causales. Leurs transformées de \textit{Laplace} respectives sont notées et . L'original est noté , et tel que :
Dans ce cas, l'original s'exprime symboliquement comme étant le produit de convolution, noté , des deux fonctions causales et . On a alors :
Dans ce cas, l'original s'exprime symboliquement comme étant le produit de convolution, noté , des deux fonctions causales et . On a alors :
Question 18
Préciser le donné à l'opération qui vous à permis de traiter correctement le de deux transformées de .
Correction
Le nom donné à l'opération qui permet de traiter correctement le de deux transformées de est (on parle également de "produit de recouvrement").
Question 19
Déterminer l'expression de l'image en y faisant apparaître et .
Correction
On a l'équation différentielle suivante :
En prenant la transformée de \textit{Laplace} de chaque terme, on obtient :
En tenant compte des conditions initiales, on trouve que :
A savoir :
Donc, on obtient :
Donc, l'image associée à cette situation est :
Soit encore :
Finalement, on obtient :
En prenant la transformée de \textit{Laplace} de chaque terme, on obtient :
En tenant compte des conditions initiales, on trouve que :
A savoir :
Donc, on obtient :
Donc, l'image associée à cette situation est :
Soit encore :
Finalement, on obtient :
Question 20
En déduire l'expression formelle (sous forme d'une intégrale) de la solution recherchée.
Vous pourrez introduire la variable temporelle .
Vous pourrez introduire la variable temporelle .
Correction
On a :
Donc, avec , on en déduit immédiatement que :
Or, d'après la question 1. de cette dernière partie, on peut donc écrire que :
Et de fait :
Ainsi, en introduisant la variable temporelle , on en déduit l'expression l'intégrale (associé au produit de convolution) de la solution :
En développant l'exponentielle, on obtient donc :
Finalement, comme l'intégration porte sur la variable muette , on trouve que :
Cependant, comme , il est donc possible d'écrire que la solution recherchée puisse également s'écrire comme :
Donc, avec , on en déduit immédiatement que :
Or, d'après la question 1. de cette dernière partie, on peut donc écrire que :
Et de fait :
Ainsi, en introduisant la variable temporelle , on en déduit l'expression l'intégrale (associé au produit de convolution) de la solution :
En développant l'exponentielle, on obtient donc :
Finalement, comme l'intégration porte sur la variable muette , on trouve que :
Cependant, comme , il est donc possible d'écrire que la solution recherchée puisse également s'écrire comme :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.