Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 17 - Exercice 1
1 h
90
On donne la table des Transformées de Laplace suivante
Question 1
On considère une fonction , telle que , au moins de classe sur .
Soit , et , trois nombres réels strictement positifs.
En outre on a .
La fonction causale satisfait à l'équation différentielle suivante :
avec les conditions initiales :
La , notée en abrégée, est symboliquement notée :
Soit , et , trois nombres réels strictement positifs.
En outre on a .
La fonction causale satisfait à l'équation différentielle suivante :
avec les conditions initiales :
La , notée en abrégée, est symboliquement notée :
Résoudre entièrement l'équation différentielle .
Correction
La appliquée à l'équation différentielle nous donne :
Ce qui nous donne :
Soit :
Ce qui nous donne :
Ainsi :
Soit encore :
Or, on a :
Ce qui nous permet d'écrire que :
Ou encore :
Avec l'aide de la table des , on a :
Ce qui nous donne :
Ce qui nous donne :
Soit :
Ce qui nous donne :
Ainsi :
Soit encore :
Or, on a :
Ce qui nous permet d'écrire que :
Ou encore :
Avec l'aide de la table des , on a :
Ce qui nous donne :
Question 2
On pose , avec qui est une quantité réelle strictement positive. Dans ce cas, montrer que :
Correction
On pose . Dans ce cas on a :
Soit :
Soit encore :
Or, on sait que :
Ce qui nous permet d'écrire que :
En développant :
Ce qui nous donne bien, par factorisations élémentaires, le résultat proposé :
Soit :
Soit encore :
Or, on sait que :
Ce qui nous permet d'écrire que :
En développant :
Ce qui nous donne bien, par factorisations élémentaires, le résultat proposé :
Question 3
On pose : . Démontrer que :
Correction
On pose :
On sait que lorsque , on a et . Dans ce cas, on obtient :
Ainsi, on obtient :
Mais, on se trouve dans la cas ou . Donc, on obtient :
En simplifiant, on obtient la forme suivante :
D'où la forme finale suivante, celle proposée par le sujet, à savoir :
On sait que lorsque , on a et . Dans ce cas, on obtient :
Ainsi, on obtient :
Mais, on se trouve dans la cas ou . Donc, on obtient :
En simplifiant, on obtient la forme suivante :
D'où la forme finale suivante, celle proposée par le sujet, à savoir :
Question 4
On pose les valeurs numériques suivantes :
;
;
Laquelle des deux représentations graphiques sur l'intervalle , proposées ci-dessous, représente l'expression ? Vous justifierez votre choix de réponse.
Propositions :
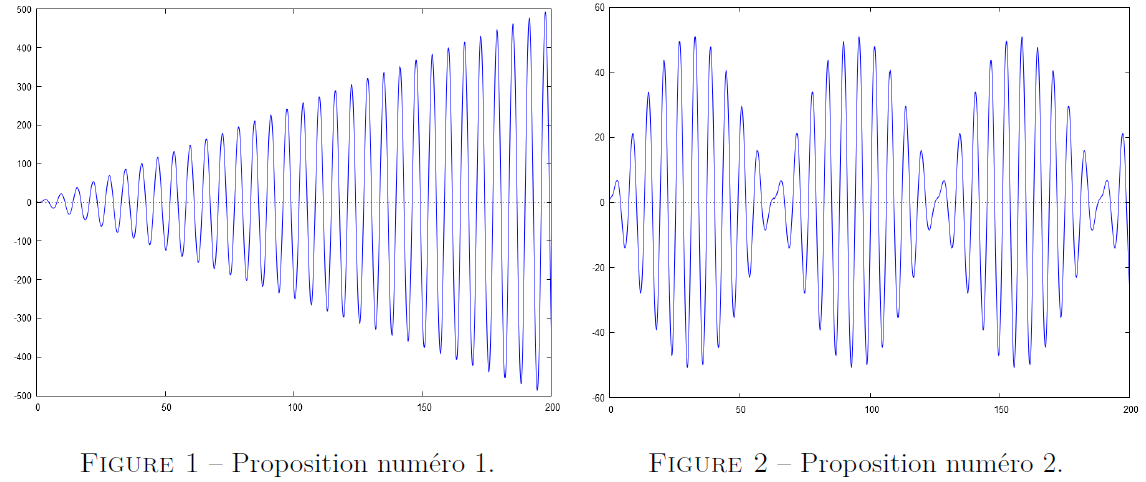
;
;
Laquelle des deux représentations graphiques sur l'intervalle , proposées ci-dessous, représente l'expression ? Vous justifierez votre choix de réponse.
Propositions :

Correction
La représentation graphique, sur l'intervalle , à retenir pour l'expression est celle de gauche, à savoir la Proposition numéro 1.
En effet, on y constate une amplitude maximale et qui est strictement croissante et linéaire.
Le phénomène mécanique qui est ici mis en évidence par est la .
En effet, on y constate une amplitude maximale et qui est strictement croissante et linéaire.
Le phénomène mécanique qui est ici mis en évidence par est la .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.