Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercice 16 - Exercice 1
50 min
75
Une situation sympathique !
Question 1
Soit un nombre réel strictement positif.
Soit un nombre réel strictement positif.
Soient et deux nombres réels.
Soit un nombre réel tel que .
Soit une fonction numérique univariée causale au moins quatre fois dérivables sur .
Cette fonction satisfait aux deux conditions limites suivantes :
;
;
;
;
.
En outre, la fonction vérifie l'équation différentielle suivante :
.
Soit un nombre réel strictement positif.
Soient et deux nombres réels.
Soit un nombre réel tel que .
Soit une fonction numérique univariée causale au moins quatre fois dérivables sur .
Cette fonction satisfait aux deux conditions limites suivantes :
;
;
;
;
.
En outre, la fonction vérifie l'équation différentielle suivante :
.
Déterminer la fonction correspondante.
Correction
On a l'équation différentielle suivante :
Soit :
Prenons la transformée de Laplace des deux membres de cette équation différentielle :
Par linéarité, on a alors :
Adoptons la notation usuelle, à savoir . On a alors :
En faisant usage des conditions initiales, on obtient :
Soit :
Soit encore :
De fait, on a :
Mais, d'après les tables de correspondances relatives à la transformation de Laplace, on sait que :
De fait, en se souvenant que , on peut donc écrire que :
D'où :
Ainsi :
Par linéarité de la transformation de Laplace, on a :
Nous sommes donc conduit à pouvoir écrire que :
En factorisant par , on obtient :
En factorisant par , on obtient :
Mais, on sait que . Donc :
Comme n'est pas nul, d'après l'énoncé, on en déduit alors que :
Puis, comme alors on a :
Puis :
Mais, le sujet nous apprend que . Donc :
Comme n'est pas nul, d'après l'énoncé, on en déduit alors que :
Ceci nous permet d'affirmer que et ainsi . Dès lors, on a alors :
Ce qui implique que . De cela, il nous est maintenant possible d'écrire que :
Soit :
En factorisant par , on obtient :
On constate que le polynôme admet comme racine évidente. Ainsi nous allons pouvoir factoriser ce polynôme par le facteur . Avec les trois réels , et on a :
En développant le membre de droite, on obtient :
Soit :
Soit encore :
Par identification, on a donc le système suivant :
Ce qui nous permet d'obtenir :
Donc :
On peut donc écrire que :
Ainsi, on obtient l'expression, de la fonction , suivante :
Finalement, en faisant explicitement apparaitre le caractère causal de la fonction recherchée, au travers de l'introduction de l'échelon unité , on trouve que :
Soit :
Prenons la transformée de Laplace des deux membres de cette équation différentielle :
Par linéarité, on a alors :
Adoptons la notation usuelle, à savoir . On a alors :
En faisant usage des conditions initiales, on obtient :
Soit :
Soit encore :
De fait, on a :
Mais, d'après les tables de correspondances relatives à la transformation de Laplace, on sait que :
De fait, en se souvenant que , on peut donc écrire que :
D'où :
Ainsi :
Par linéarité de la transformation de Laplace, on a :
Nous sommes donc conduit à pouvoir écrire que :
En factorisant par , on obtient :
En factorisant par , on obtient :
Mais, on sait que . Donc :
Comme n'est pas nul, d'après l'énoncé, on en déduit alors que :
Puis, comme alors on a :
Puis :
Mais, le sujet nous apprend que . Donc :
Comme n'est pas nul, d'après l'énoncé, on en déduit alors que :
Ceci nous permet d'affirmer que et ainsi . Dès lors, on a alors :
Ce qui implique que . De cela, il nous est maintenant possible d'écrire que :
Soit :
En factorisant par , on obtient :
On constate que le polynôme admet comme racine évidente. Ainsi nous allons pouvoir factoriser ce polynôme par le facteur . Avec les trois réels , et on a :
En développant le membre de droite, on obtient :
Soit :
Soit encore :
Par identification, on a donc le système suivant :
Ce qui nous permet d'obtenir :
Donc :
On peut donc écrire que :
Ainsi, on obtient l'expression, de la fonction , suivante :
Finalement, en faisant explicitement apparaitre le caractère causal de la fonction recherchée, au travers de l'introduction de l'échelon unité , on trouve que :
Question 2
Dans le cas de , représenter graphiquement l'expression .
Correction
Lorsque l'on pose , on obtient l'expression suivante :
Ce qui nous donne donc :
Graphiquement, on obtient la figure suivante :
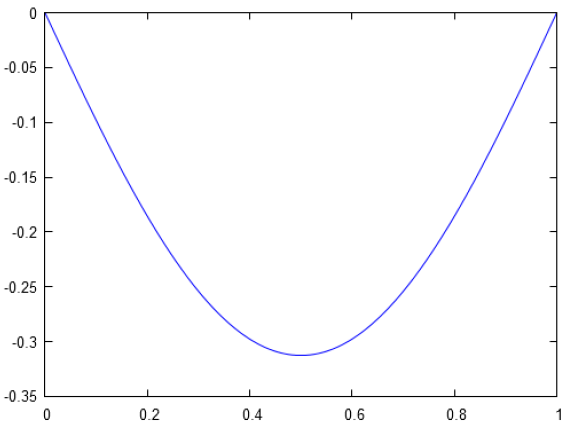
REMARQUE :
Cet exercice illustre et décrit la situation d'une poutre homogène chargée uniformément (la déformée en R.D.M.) sur deux appuis pivotants dans le plan.
Ce qui nous donne donc :
Graphiquement, on obtient la figure suivante :

REMARQUE :
Cet exercice illustre et décrit la situation d'une poutre homogène chargée uniformément (la déformée en R.D.M.) sur deux appuis pivotants dans le plan.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.