Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Intégration
Intégrale d'une fonction en escalier.
Subdivision
Soit un nombre entier naturel non nul.
On appelle de l'intervalle réel la donnée d'un nombre fini de points tel que , et .
On note par l'ensemble de toutes des subdivisions de l'intervalle réel .
Le d'une subdivision est le nombre réel .
On appelle de l'intervalle réel la donnée d'un nombre fini de points tel que , et .
On note par l'ensemble de toutes des subdivisions de l'intervalle réel .
Le d'une subdivision est le nombre réel .
Fonction en escalier
Un fonction numérique univariée , définie sur l'intervalle réel , est une s'il existe telle que soit constante, et égale à , sur chaque intervalle ouvert .
Intégrale d'une fonction en escalier
On appelle de la fonction en escalier , le nombre :
Ce nombre est également noté :
Ce nombre est également noté :
Intégrale d'une fonction continue par morceaux
Fonction continue par morceaux
Une fonction , définie sur l'intervalle , est une sur s'il existe telle que soit continue sur chaque intervalle ouvert et que admette, en tout point de la subdivision, une limite finie à gauche et une limite finie à droite.
Approximation par une fonction en escalier
Soit une fonction continue par morceaux sur l'intervalle .
Pour tout nombre réel strictement positif, il existe les deux fonctions et en escalier sur telles que :
Pour tout nombre réel strictement positif, il existe les deux fonctions et en escalier sur telles que :
Approximation par une fonction en escalier
Soit une fonction continue par morceaux sur l'intervalle .
Il existe un nombre réel unique tel que, pour toutes fonctions en escaliers sur et vérifiant , on ait :
Ce nombre s'appelle de sur , et se note , ou , ou , ou . Ce nombre dépend donc de , de , de mais pas de la variable d'intégration, notée ici . Cette variable d'intégration est dite ce qui signifie que l'on peut la noter par toute lettre non retenue pour un autre usage.
Pour , on pose :
Puis pour on a :
Il existe un nombre réel unique tel que, pour toutes fonctions en escaliers sur et vérifiant , on ait :
Ce nombre s'appelle de sur , et se note , ou , ou , ou . Ce nombre dépend donc de , de , de mais pas de la variable d'intégration, notée ici . Cette variable d'intégration est dite ce qui signifie que l'on peut la noter par toute lettre non retenue pour un autre usage.
Pour , on pose :
Puis pour on a :
Interprétation géométrique
Le nombre réel représente l'aire du domaine du plan situé sour la courbe représentative de et entre les abscisses et :
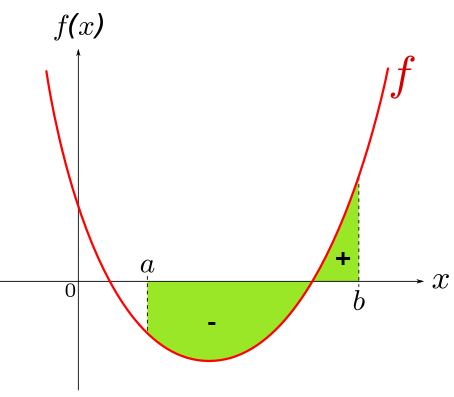
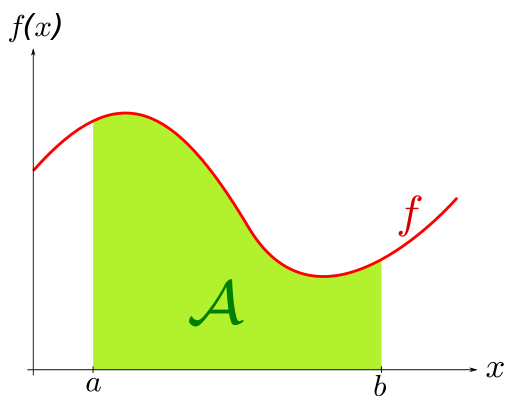 Ce nombre est compté positivement si la courbe est au-dessus de l'axe des abscisses et ce nombre est compté négativement si la courbe est au-dessus de l'axe des abscisses :
Ce nombre est compté positivement si la courbe est au-dessus de l'axe des abscisses et ce nombre est compté négativement si la courbe est au-dessus de l'axe des abscisses :
 Le nombre réel représente l'aire du domaine du plan situé sour la courbe représentative de et entre les abscisses et . En fait, ce nombre représente la somme des aires infinitésimales (infiniment petites), notée , de rectangles infinitésimaux dont, à l'abscisse , la hauteur est donnée par et la largeur infinitésimale est donnée par . On a alors :
Le nombre réel représente l'aire du domaine du plan situé sour la courbe représentative de et entre les abscisses et . En fait, ce nombre représente la somme des aires infinitésimales (infiniment petites), notée , de rectangles infinitésimaux dont, à l'abscisse , la hauteur est donnée par et la largeur infinitésimale est donnée par . On a alors :
Ceci est représentée sur la figure suivante :
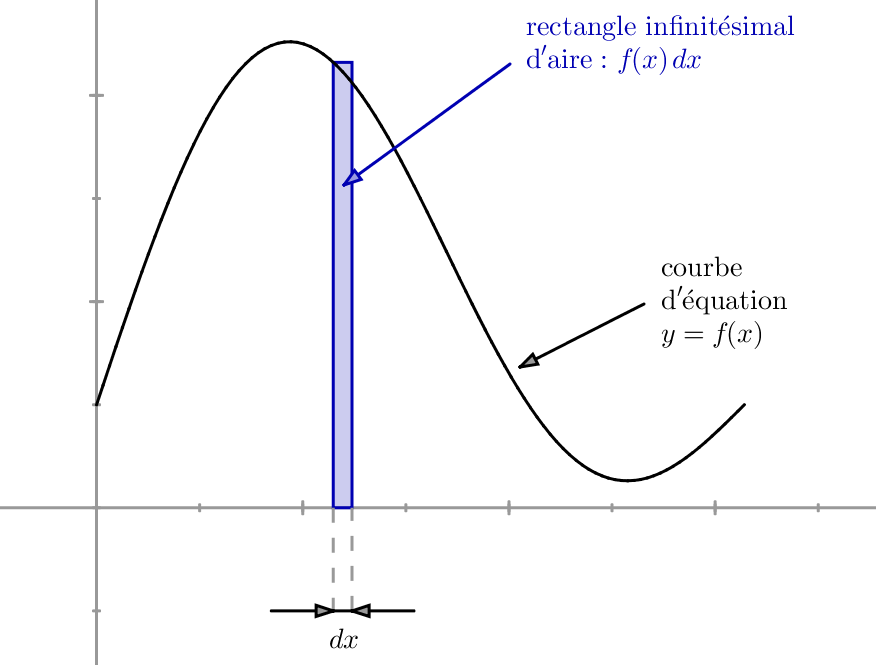


Ceci est représentée sur la figure suivante :

Propriétés d'une intégrale
On considère les deux fonctions numériques réelles, de dans , qui sont continues par morceaux sur les intervalles considérés.Soit un nombre réel. On a :
Et aussi :
On a la relation suivante :
Si , et si sur l'intervalle , alors on a :
Si est une fonction numérique réelle, continue et sur l'intervalle , alors on a l'équivalence suivante :
Si alors on a :
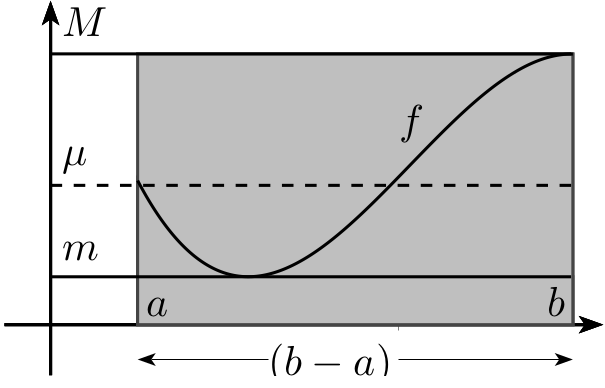
Soit une fonction numérique continue sur l'intervalle .
Le nombre représente la valeur moyenne de la fonction sur l'intervalle .
Soit et deux nombres réels tels que .
Si, pour tout nombre réel de l'intervalle on a , alors on a :
Ceci s'illustre par :
Si alors on a :
Et en particulier si :
L'application définit un produit scalaire sur l'espace vectoriel des fonctions réelles continues sur l'intervalle .
L'inégalité de est la suivante :
On considère les deux fonctions réelles continues sur l'intervalle .
On a l'inégalité suivante :
Soit un nombre entier naturel non nul. On a l'égalité suivante :
Plus généralement, si est une subdivision de l'intervalle dont le pas tend vers zéro lorsque tend vers l'infini, et un point quelconque de l'intervalle , on a alors l'égalité suivante :
Intégrale d'une fonction continue par morceaux à valeurs complexes .
Soit le nombre complexe qui satisfait à .
Soit une fonction de dans , définie sur l'intervalle .
Si les deux fonctions et sont continues par morceaux sur l'intervalle alors la fonction l'est également.
L'intégrale de sur l'intervalle est donnée par :
Toutes les propriétés de l'intégrale d'une fonction numérique continue par morceaux, à valeurs réelles, qui ont encore un sens, sont prolongées. Donc on conserve la linéarité, la relation de Chasles et la majoration du module de l'intégrale qui s'exprime comme :
Mais , n'oubliez pas que la relation d'ordre n'a pas de sens dans ! Ceci fait qu'il n'y a strictement aucun sens, dans , d'écrire ou .
Soit une fonction de dans , définie sur l'intervalle .
Si les deux fonctions et sont continues par morceaux sur l'intervalle alors la fonction l'est également.
L'intégrale de sur l'intervalle est donnée par :
Toutes les propriétés de l'intégrale d'une fonction numérique continue par morceaux, à valeurs réelles, qui ont encore un sens, sont prolongées. Donc on conserve la linéarité, la relation de Chasles et la majoration du module de l'intégrale qui s'exprime comme :
Mais , n'oubliez pas que la relation d'ordre n'a pas de sens dans ! Ceci fait qu'il n'y a strictement aucun sens, dans , d'écrire ou .
Calcul numérique d'une intégrale .
Le calcul de l'intégrale est souvent très difficile, sinon impossible même. On peut cependant obtenir des valeurs approchées de par diverses méthodes. Nous en présentons, ici, deux particulièrement simples.
Cette méthode consiste à approcher par une fonction en escalier (d'où l'apparition de rectangles).
On partage l'intervalle d'intégration en segments de même longueur, notée , et qui s'exprime comme :
On obtient la valeur approchée, notée , de suivante :
Lorsque la fonction possède une fonction dérivée bornée sur l'intervalle d'intégration , on majore l'erreur commise, en approchant par , par la relation suivante :
Ou encore :
Cette majoration permet, en autre, de déterminer le nombre qui permet de satisfaire à un choix de précision souhaité au préalable.
Si est croissante sur l'intervalle d'intégration alors l'approximation est une valeur approchée par défaut.
Si est décroissante sur l'intervalle d'intégration alors l'approximation est une valeur approchée par excès.
Cette méthode des rectangles se représente par le découpage suivant :

Cette méthode consiste à approcher le graphique de par une ligne polygonale (d'où l'apparition de trapèzes).
On partage l'intervalle d'intégration en segments de même longueur, notée , et qui s'exprime comme :
On obtient la valeur approchée, notée , de suivante :
Lorsque la fonction possède une fonction dérivée seconde bornée sur l'intervalle d'intégration , on majore l'erreur commise, en approchant par , par la relation suivante :
Ou encore :
Cette majoration permet, en autre, de déterminer le nombre qui permet de satisfaire à un choix de précision souhaité au préalable.
Si est convexe sur l'intervalle d'intégration alors (l'approximation , de , est par excès). Si la dérivée seconde existe sur l'intervalle d'intégration , alors est convexe lorsque .
Si est concave sur l'intervalle d'intégration alors (l'approximation , de , est par défaut). Si la dérivée seconde existe sur l'intervalle d'intégration , alors est concave lorsque .
Cette méthode des trapèzes se représente par le découpage suivant :

Cette méthode consiste à approcher la courbe représentative de par une succession d'arcs de paraboles d'équations . A chaque fois, donc sur chaque segment de découpage, les trois coefficients réels , et se déterminent par les trois conditions :
Dans cette méthode de , on partage l'intervalle d'intégration en segments de même longueur, notée , et qui s'exprime comme :
On obtient la valeur approchée, notée , de suivante :
Lorsque la fonction possède une fonction dérivée quatrième bornée sur l'intervalle d'intégration , on majore l'erreur commise, en approchant par , par la relation suivante :
Ou encore :
Cette majoration permet, en autre, de déterminer le nombre qui permet de satisfaire à un choix de précision souhaité au préalable.
Cette méthode de se représente par le découpage qui est explicité sur la figure suivante avec la situation . On a donc segments de découpage de l'intervalle qui sont , , et , et dont les milieux respectifs sont , , et . D'où :
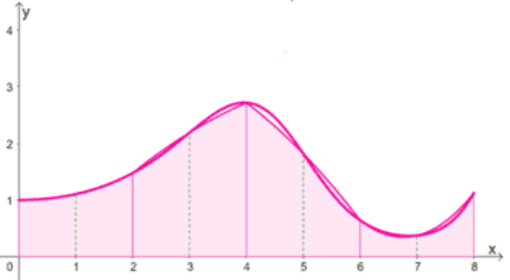
Cette méthode consiste à approcher par une fonction en escalier (d'où l'apparition de rectangles).
On partage l'intervalle d'intégration en segments de même longueur, notée , et qui s'exprime comme :
On obtient la valeur approchée, notée , de suivante :
Lorsque la fonction possède une fonction dérivée bornée sur l'intervalle d'intégration , on majore l'erreur commise, en approchant par , par la relation suivante :
Ou encore :
Cette majoration permet, en autre, de déterminer le nombre qui permet de satisfaire à un choix de précision souhaité au préalable.
Si est croissante sur l'intervalle d'intégration alors l'approximation est une valeur approchée par défaut.
Si est décroissante sur l'intervalle d'intégration alors l'approximation est une valeur approchée par excès.
Cette méthode des rectangles se représente par le découpage suivant :

Cette méthode consiste à approcher le graphique de par une ligne polygonale (d'où l'apparition de trapèzes).
On partage l'intervalle d'intégration en segments de même longueur, notée , et qui s'exprime comme :
On obtient la valeur approchée, notée , de suivante :
Lorsque la fonction possède une fonction dérivée seconde bornée sur l'intervalle d'intégration , on majore l'erreur commise, en approchant par , par la relation suivante :
Ou encore :
Cette majoration permet, en autre, de déterminer le nombre qui permet de satisfaire à un choix de précision souhaité au préalable.
Si est convexe sur l'intervalle d'intégration alors (l'approximation , de , est par excès). Si la dérivée seconde existe sur l'intervalle d'intégration , alors est convexe lorsque .
Si est concave sur l'intervalle d'intégration alors (l'approximation , de , est par défaut). Si la dérivée seconde existe sur l'intervalle d'intégration , alors est concave lorsque .
Cette méthode des trapèzes se représente par le découpage suivant :

Cette méthode consiste à approcher la courbe représentative de par une succession d'arcs de paraboles d'équations . A chaque fois, donc sur chaque segment de découpage, les trois coefficients réels , et se déterminent par les trois conditions :
Dans cette méthode de , on partage l'intervalle d'intégration en segments de même longueur, notée , et qui s'exprime comme :
On obtient la valeur approchée, notée , de suivante :
Lorsque la fonction possède une fonction dérivée quatrième bornée sur l'intervalle d'intégration , on majore l'erreur commise, en approchant par , par la relation suivante :
Ou encore :
Cette majoration permet, en autre, de déterminer le nombre qui permet de satisfaire à un choix de précision souhaité au préalable.
Cette méthode de se représente par le découpage qui est explicité sur la figure suivante avec la situation . On a donc segments de découpage de l'intervalle qui sont , , et , et dont les milieux respectifs sont , , et . D'où :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.