Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Eléments fondamentaux - Exercice 1
40 min
60
Illustrons, dans un cas très simple, donc très pédagogique, les différentes approches numériques du calcul approchée d'une intégrale.
On note par la fonction suivante :
On pose alors :
On note par la fonction suivante :
On pose alors :
Question 1
Calculer la valeur de par la méthode usuelle des primitives.
Correction
On sait que la fonction exponentielle est définie sur tout entier, et qu'elle y est infiniment dérivable, et de fait elle y est continue.
En outre, on sait que :
Donc :
Finalement :
De manière approchée, on a :
Graphiquement, cela nous donne :
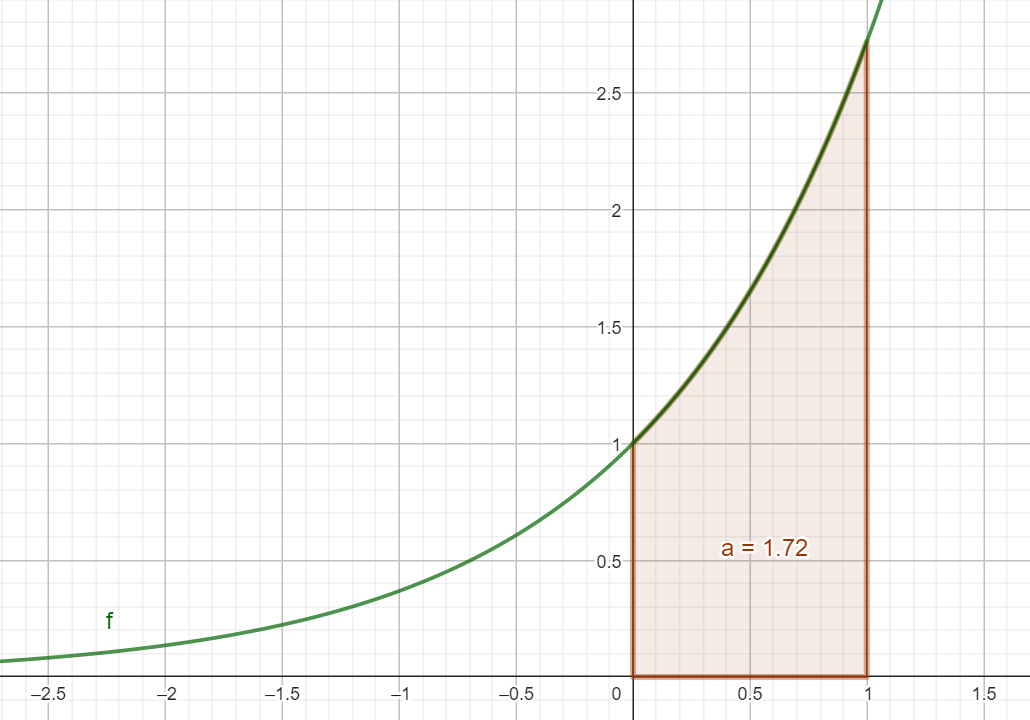
En outre, on sait que :
Donc :
Finalement :
De manière approchée, on a :
Graphiquement, cela nous donne :

Question 2
Calculer la valeur de par une somme de .
Correction
On sait que :
Dans notre cas, ceci nous donne :
Soit :
Et on a :
Il s'agit de la somme des premiers termes d'une suite géométrique de premier terme et de raison . On a alors :
Soit :
Ceci nous permet d'écrire que :
Posons . Si alors . Donc :
Or, lorsque on a l'équivalence suivante :
Donc :
Finalement, on a bien :
Dans notre cas, ceci nous donne :
Soit :
Et on a :
Il s'agit de la somme des premiers termes d'une suite géométrique de premier terme et de raison . On a alors :
Soit :
Ceci nous permet d'écrire que :
Posons . Si alors . Donc :
Or, lorsque on a l'équivalence suivante :
Donc :
Finalement, on a bien :
Question 3
Calculer, avec une précision meilleure que le millième, la valeur approchée de par la méthode numérique des rectangles.
Correction
On sait que la fonction exponentielle est définie sur tout entier, et qu'elle y est infiniment dérivable, et de fait elle y est continue.
En outre, on sait que :
Donc . Ce qui implique que est croissante sur l'intervalle d'intégration , et de fait :
De plus, on sait que :
Donc, pour notre situation :
Comme on désire la valeur approchée de , meilleure que le millième, on a donc :
Ce qui nous permet de choisir car . Et on a alors :
On a alors :
Soit :
On constate la présence de la somme des premiers termes d'une suite géométrique de premier terme et de raison . On a alors :
Soit :
De manière approchée, on a :
En outre, on sait que :
Donc . Ce qui implique que est croissante sur l'intervalle d'intégration , et de fait :
De plus, on sait que :
Donc, pour notre situation :
Comme on désire la valeur approchée de , meilleure que le millième, on a donc :
Ce qui nous permet de choisir car . Et on a alors :
On a alors :
Soit :
On constate la présence de la somme des premiers termes d'une suite géométrique de premier terme et de raison . On a alors :
Soit :
De manière approchée, on a :
Question 4
Calculer, avec une précision meilleure que le millième, la valeur approchée de par la méthode numérique des trapèzes.
Correction
On sait que la fonction exponentielle est définie sur tout entier, et qu'elle y est infiniment dérivable, et de fait elle y est continue.
En outre, on sait que :
Donc . Ce qui implique que est croissante sur l'intervalle d'intégration , et de fait :
De plus, on sait que :
Donc, pour notre situation :
Comme on désire la valeur approchée de , meilleure que le millième, on a donc :
Soit . Ce qui nous permet de choisir car . Et on a alors :
On a alors :
Avec :
Il s'agit de la somme des premiers termes d'une suite géométrique de premier terme et de raison . On a alors :
Donc :
Ainsi :
De manière approchée :
En outre, on sait que :
Donc . Ce qui implique que est croissante sur l'intervalle d'intégration , et de fait :
De plus, on sait que :
Donc, pour notre situation :
Comme on désire la valeur approchée de , meilleure que le millième, on a donc :
Soit . Ce qui nous permet de choisir car . Et on a alors :
On a alors :
Avec :
Il s'agit de la somme des premiers termes d'une suite géométrique de premier terme et de raison . On a alors :
Donc :
Ainsi :
De manière approchée :
Question 5
Calculer, avec une précision meilleure que le millième, la valeur approchée de par la méthode numérique de .
Correction
On sait que la fonction exponentielle est définie sur tout entier, et qu'elle y est infiniment dérivable, et de fait elle y est continue.
En outre, on sait que :
Donc . Ce qui implique que est croissante sur l'intervalle d'intégration , et de fait :
De plus, on sait que :
Donc, pour notre situation :
Comme on désire la valeur approchée de , meilleure que le millième, on a donc :
Soit , d'où . Ce qui nous permet de choisir car . Et on a alors :
De plus, on sait que, de manière générale, on a :
Dans notre cas à nous , on obtient donc :
On constate que la dernière somme n'existe pas. De fait, on obtient :
Puis, on constate également que :
Ainsi, on trouve que :
De manière approchée, on obtient :
En outre, on sait que :
Donc . Ce qui implique que est croissante sur l'intervalle d'intégration , et de fait :
De plus, on sait que :
Donc, pour notre situation :
Comme on désire la valeur approchée de , meilleure que le millième, on a donc :
Soit , d'où . Ce qui nous permet de choisir car . Et on a alors :
De plus, on sait que, de manière générale, on a :
Dans notre cas à nous , on obtient donc :
On constate que la dernière somme n'existe pas. De fait, on obtient :
Puis, on constate également que :
Ainsi, on trouve que :
De manière approchée, on obtient :
Question 6
Quelle(s) conclusion(s) pouvez-vous faire à partir de cet exemple simple ?
Correction
On constate que :
- la méthode de est celle qui est la plus rapide à mettre oeuvre ;
- la méthode des rectangles est celle qui est la plus intuitive mais la moins rapide à mettre oeuvre ;
- La méthode par les sommes de s'avère plus technique ;
- toutes ces approches sont parfaitement cohérentes entre-elles.
Il existe d'autres méthode, citons par exemple :
- la méthode des tangentes ;
- la méthode de ;
- la méthode de ;
- la méthode de ;
- la méthode de .
- la méthode de est celle qui est la plus rapide à mettre oeuvre ;
- la méthode des rectangles est celle qui est la plus intuitive mais la moins rapide à mettre oeuvre ;
- La méthode par les sommes de s'avère plus technique ;
- toutes ces approches sont parfaitement cohérentes entre-elles.
Il existe d'autres méthode, citons par exemple :
- la méthode des tangentes ;
- la méthode de ;
- la méthode de ;
- la méthode de ;
- la méthode de .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.