Les suites
Exercice 6 - Exercice 1
1 min
0
Des Suites avec des Logarithmes :)
Question 1
On appelle la fonction définie sur l'intervalle par . On note la courbe représentative de la fonction .
On considère également une fonction définie sur l'intervalle par .
On considère également une fonction définie sur l'intervalle par .
Calculer la limite de la fonction en .
Correction
Ici, il s'agit d'une limite par composition.
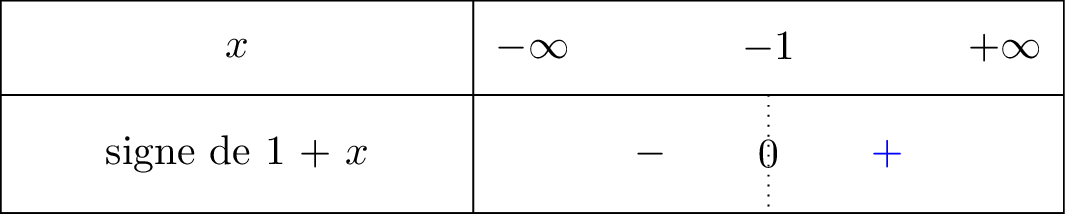
On commence par calculer . Le tableau de signe ci-dessous nous explique pourquoi
 On pose .
On pose .
Ainsi : .
Par composition :
Ainsi :
On commence par calculer . Le tableau de signe ci-dessous nous explique pourquoi

Ainsi : .
Par composition :
Ainsi :
Question 2
Calculer la limite de la fonction en .
Correction
Question 3
On note la fonction dérivée de . Calculer pour tout de l’intervalle .
Correction
Soit .
est dérivable sur .
est dérivable sur .
Question 4
Etudier les variations de la fonction sur l'intervalle .
Correction
Il nous faut étidier le signe de :
Comme alors et donc . Le dénominateur est donc strictement positif.
De plus, nous savons que ainsi . De ce fait , , ce qui signifie que le numérateur est positif.
Il en résulte donc que :
. Ce qui signifie que la fonction est strictement croissante sur .
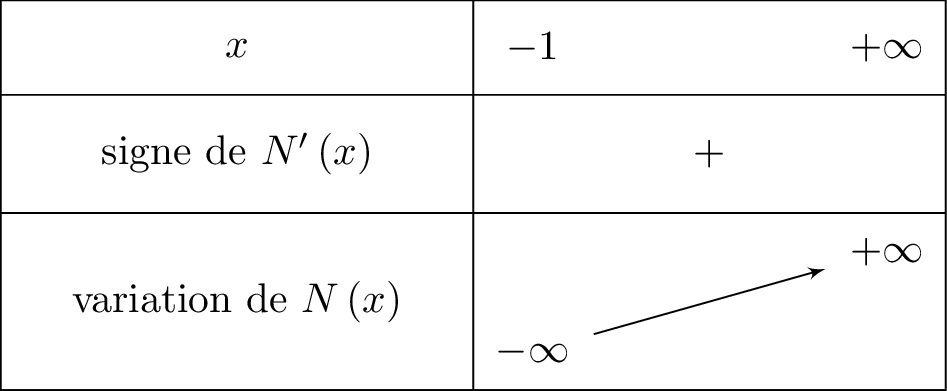
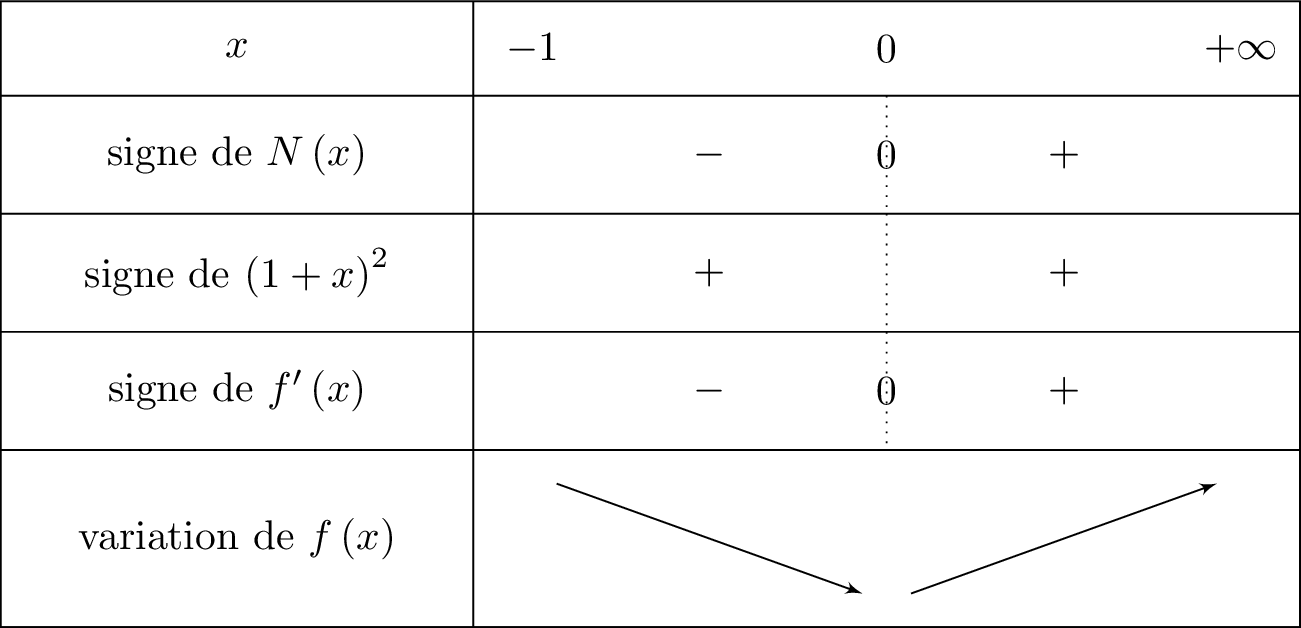
Nous dressons ci-dessous, le tableau de variation de la fonction en y intégrant les limites déterminées précédemment.
Comme alors et donc . Le dénominateur est donc strictement positif.
De plus, nous savons que ainsi . De ce fait , , ce qui signifie que le numérateur est positif.
Il en résulte donc que :
. Ce qui signifie que la fonction est strictement croissante sur .
Nous dressons ci-dessous, le tableau de variation de la fonction en y intégrant les limites déterminées précédemment.

Question 5
Calculer et en déduire le signe de sur l'intervalle .
Correction
Soit ainsi :
d'où
Il vient que :
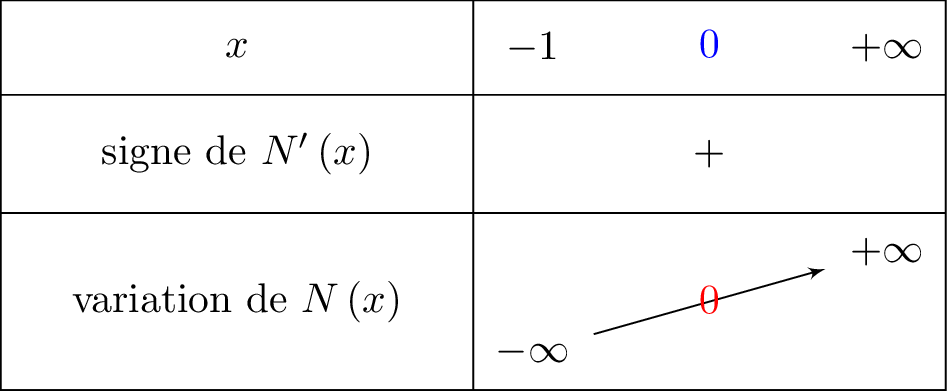
Sur , la fonction est continue et strictement croissante.
De plus, et
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que et nous savons que .
Sur , la fonction est continue et strictement croissante et
Donc pour tout et pour tout
On résume cela dans un tableau de signe :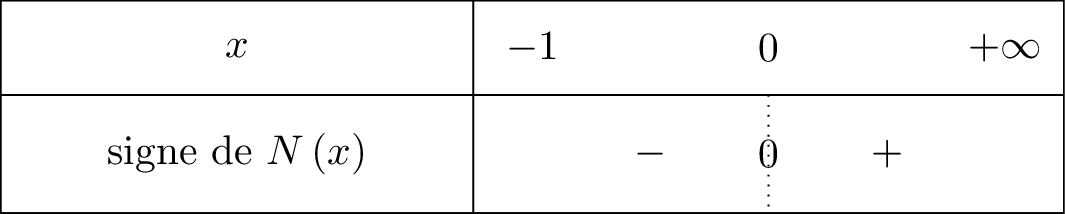
d'où
Il vient que :
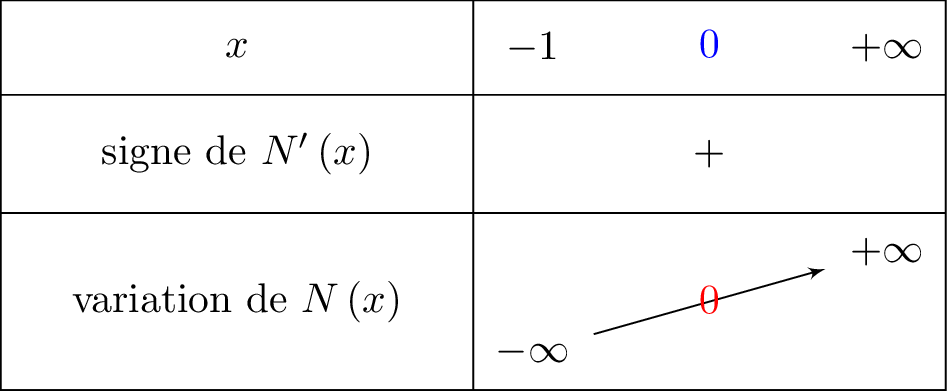
De plus, et
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que et nous savons que .
Sur , la fonction est continue et strictement croissante et
Donc pour tout et pour tout
On résume cela dans un tableau de signe :

Question 6
On note la fonction dérivée de . Calculer pour tout de l’intervalle et montrer que
Correction
Soit
est dérivable sur .
On reconnaît la forme avec ; et .
Ainsi ; et .
est dérivable sur .
On reconnaît la forme avec ; et .
Ainsi ; et .
Question 7
En déduire les variations de la fonction . On ne demandera pas les limites.
Correction
D'après la question , nous savons que :
Or pour tout , nous vérifions facilement que ( vu aussi à la question )
Donc le signe de dépend du signe de .
Or, d'après la question , nous avons déterminer le signe de . Nous pouvons donc dresser le tableau de variation de la fonction .
Or pour tout , nous vérifions facilement que ( vu aussi à la question )
Donc le signe de dépend du signe de .
Or, d'après la question , nous avons déterminer le signe de . Nous pouvons donc dresser le tableau de variation de la fonction .

Question 8
Démontrer que si , alors .
Correction
Nous savons que les variations de la fonction dont données par le tableau ci-dessous :
 Nous allons faire une rescription de la fonction sur l'intervalle .
Nous allons faire une rescription de la fonction sur l'intervalle .
d'où d'où et Il vient alors que : 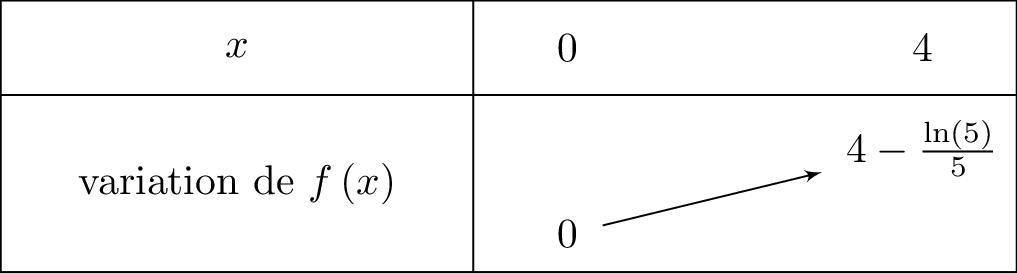 Comme alors :
Comme alors :
car la fonction est croissante sur donc l'ordre est conservé .
Ainsi si , alors .


car la fonction est croissante sur donc l'ordre est conservé .
Ainsi si , alors .
Question 9
On considère la suite définie par :
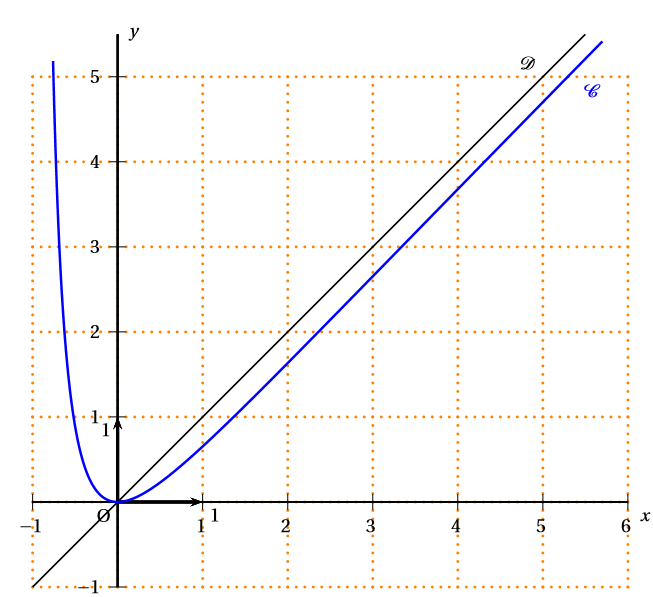

Sur le graphique ci-dessus, en utilisant la courbe et la droite , placer les points de d’abscisses , , et .
Correction
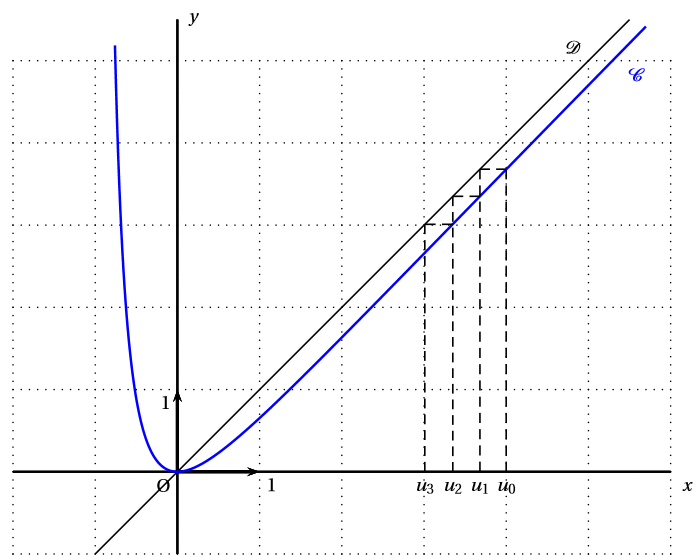
Question 10
Démontrer que pour tout entier naturel , on a :
Correction
Pour tout entier naturel , posons la propriété
Etape d'initialisation
Nous savons que et donc .
La propriété est vraie.
Etape d'hérédité
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire :
Par hypothèse de récurrence,
, or est une fonction croissante sur , ainsi :
car
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , on a :
Etape d'initialisation
Nous savons que et donc .
La propriété est vraie.
Etape d'hérédité
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire :
Par hypothèse de récurrence,
, or est une fonction croissante sur , ainsi :
car
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , on a :
Question 11
Étudier la monotonie de la suite .
Correction
Il nous faut étudier le signe de .
équivaut successivement à :
Comme alors :
Ainsi : et
Il en résulte donc que :
Par conséquent :
et donc la suite est décroissante.
équivaut successivement à :
Comme alors :
Ainsi : et
Il en résulte donc que :
Par conséquent :
et donc la suite est décroissante.
Question 12
Démontrer que la suite est convergente. On désigne par sa limite.
Correction
- Une suite décroissante et minorée est convergente, elle admet donc une limite finie.
- Une suite croissante et majorée est convergente, elle admet donc une limite finie.
D'après le théorème de convergence des suites monotones , on peut affirmer que la suite est convergente et admet donc une limite que l'on note .
Question 13
Donner alors la valeur de .
Correction
Comme est continue, on sait que est solution de l’équation . On en déduit que .
Ce calcul a été fait à la question en montrant que .
Ce calcul a été fait à la question en montrant que .