Les probabilités conditionnelles et loi binomiale
Exercice 2 - Exercice 1
1 min
0
Les parties et et sont indépendantes.
Un site internet propose des jeux en ligne.
Un site internet propose des jeux en ligne.
Question 1
Partie A
Pour un premier jeu :
Pour tout entier naturel non nul , on désigne par l'évènement « l'internaute gagne la -ième partie » et on note la probabilité de l'évènement .
L'internaute gagne toujours la première partie et donc .
Pour un premier jeu :
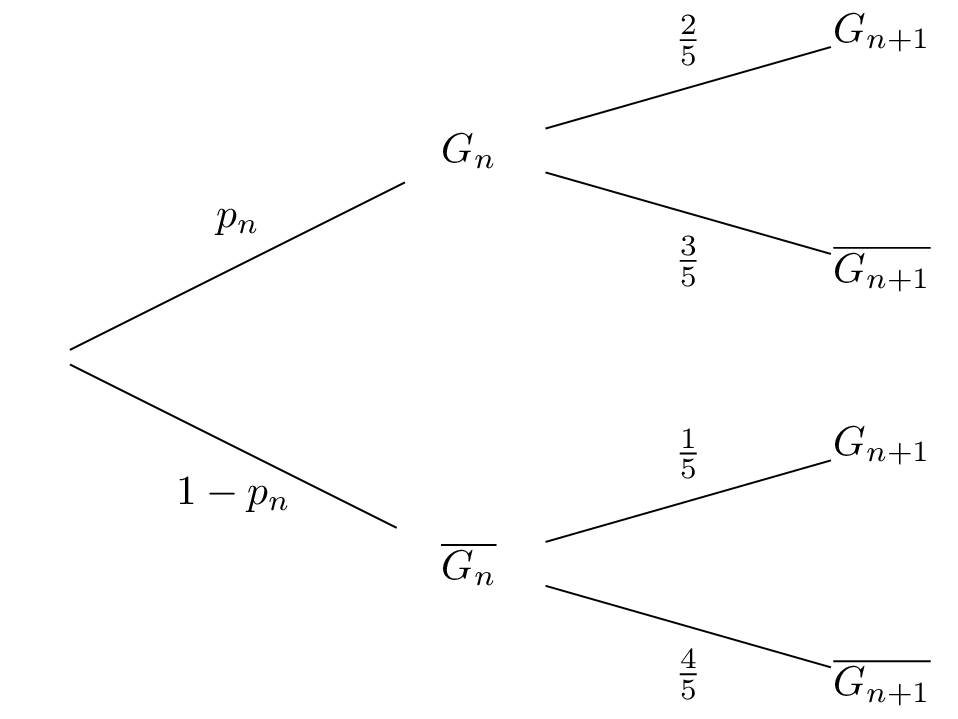
- Si l'internaute gagne une partie, la probabilité qu'il gagne la partie suivante est égale à .
- Si l'internaute perd une partie, la probabilité qu'il perde la partie suivante est égale à
Pour tout entier naturel non nul , on désigne par l'évènement « l'internaute gagne la -ième partie » et on note la probabilité de l'évènement .
L'internaute gagne toujours la première partie et donc .
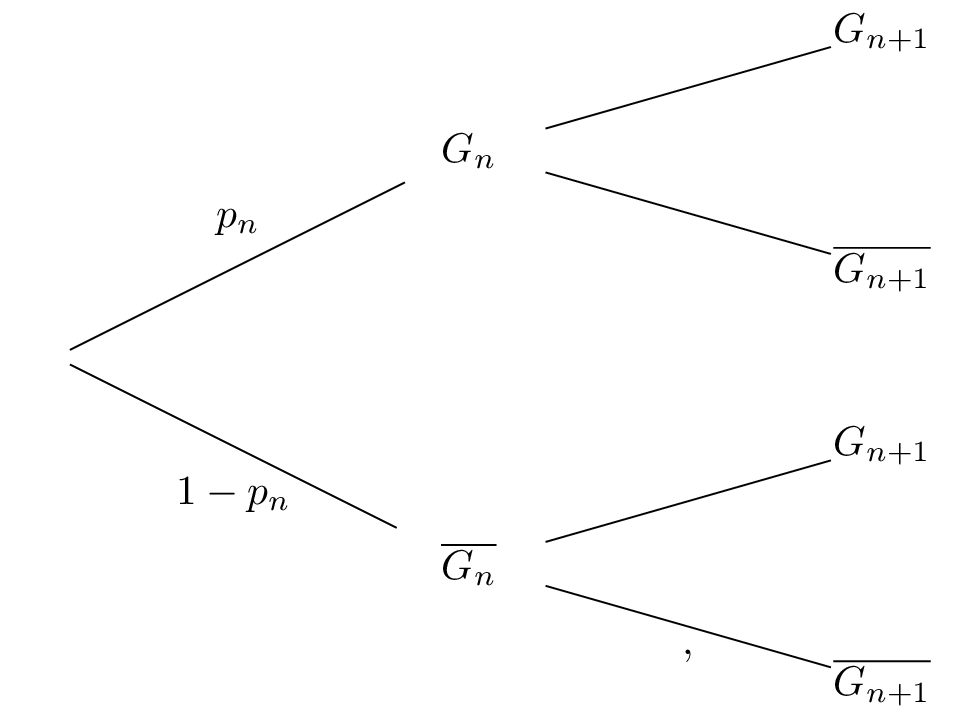
Recopier et compléter l'arbre pondéré suivant :

Correction
D'après l'énoncé, on en déduit l'arbre suivant :

Question 2
Montrer que, pour tout entier naturel non nul, .
Correction
On note la probabilité de l'évènement .
Il vient alors que la probabilité de l'évènement , c'est-à-dire : .
Les évènements et forment une partition de l'univers.
D'après la formule des probabilités totales, on a :
Il vient alors que la probabilité de l'évènement , c'est-à-dire : .
Les évènements et forment une partition de l'univers.
D'après la formule des probabilités totales, on a :
Question 3
Pour tout entier naturel non nul, on pose .
Montrer que est une suite géométrique de raison et de premier terme à préciser.
Correction
Pour tout entier naturel non nul, on a :
Or : , il vient alors :
Or : d'où :
L'égalité montre que la suite est une suite géométrique de raison et de premier terme .
Or : , il vient alors :
Or : d'où :
L'égalité montre que la suite est une suite géométrique de raison et de premier terme .
Question 4
Montrer que, pour tout entier naturel non nul, .
Correction
Commençons par exprimer en fonction de .
Pour tout naturel supérieur ou égal à :
Ensuite exprimons en fonction de .
Comme alors
On a finalement :
Pour tout naturel supérieur ou égal à :
Ensuite exprimons en fonction de .
Comme alors
On a finalement :
Question 5
Déterminer la limite de .
Correction
Comme alors et .
Il en résulte que :
Au bout d'un très grand nombre de parties, la probabilité de gagner sera proche d'une chance sur quatre.
Il en résulte que :
Au bout d'un très grand nombre de parties, la probabilité de gagner sera proche d'une chance sur quatre.
Question 6
Partie B
Dans un second jeu, le joueur doit effectuer parties.
On suppose que toutes les parties sont indépendantes.
La probabilité de gagner chaque partie est égale à .
Soit la variable aléatoire égale au nombre de parties gagnées par le joueur.
Dans un second jeu, le joueur doit effectuer parties.
On suppose que toutes les parties sont indépendantes.
La probabilité de gagner chaque partie est égale à .
Soit la variable aléatoire égale au nombre de parties gagnées par le joueur.
Quelle est la loi de probabilité suivie par la variable aléatoire ?
Justifier.
Justifier.
Correction
A chaque tirage la probabilité de gagner une partie est égale à .
On est donc en présence d'un schéma de Bernoulli :
On appelle succès « gagner une partie » avec la probabilité
On appelle échec « perdre une partie » avec la probabilité
On répète dix fois de suite cette expérience de façon indépendante.
est la variable aléatoire qui associe le nombre de parties gagnées par le joueur.
suit la loi binomiale de paramètre et .
On note alors
On est donc en présence d'un schéma de Bernoulli :
On appelle succès « gagner une partie » avec la probabilité
On appelle échec « perdre une partie » avec la probabilité
On répète dix fois de suite cette expérience de façon indépendante.
est la variable aléatoire qui associe le nombre de parties gagnées par le joueur.
suit la loi binomiale de paramètre et .
On note alors
Question 7
Quelle est la probabilité que le joueur gagne au moins une partie ?
Le résultat sera arrondi à près.
Le résultat sera arrondi à près.
Correction
A la calculatrice, on obtient :
arrondi à près.
Question 8
Déterminer l'espérance de .
Correction
est une variable aléatoire qui suit une loi binomiale , alors l’espérance mathématique , la variance et l’écart type sont égales à :
On a :Cela signifie que le joueur gagne en moyenne parties sur les parties.
Le joueur doit payer euros pour jouer les parties.
Chaque partie gagnée lui rapporte euros.
Question 9
Expliquer pourquoi ce jeu est désavantageux pour le joueur.
Correction
Le joueur doit payer euros pour les parties et récupérera en moyenne euros. (Espérance de gagner parties sur )
En moyenne les parties coûteront euros, soit euros par partie.
Le jeu est donc désavantageux.
En moyenne les parties coûteront euros, soit euros par partie.
Le jeu est donc désavantageux.
Question 10
Calculer la probabilité pour un joueur de réaliser un bénéfice supérieur à euros ?
Le résultat sera arrondi à près.
Le résultat sera arrondi à près.
Correction
Pour réaliser un bénéfice supérieur à euros, vu la mise de euros, il faut gagner plus de euros.
Comme , il faut donc gagner parties au moins sur 10 .
Comme , il faut donc gagner parties au moins sur 10 .
Question 11
Partie C
Cette partie est totalement indépendante des parties et .
Cette partie est totalement indépendante des parties et .
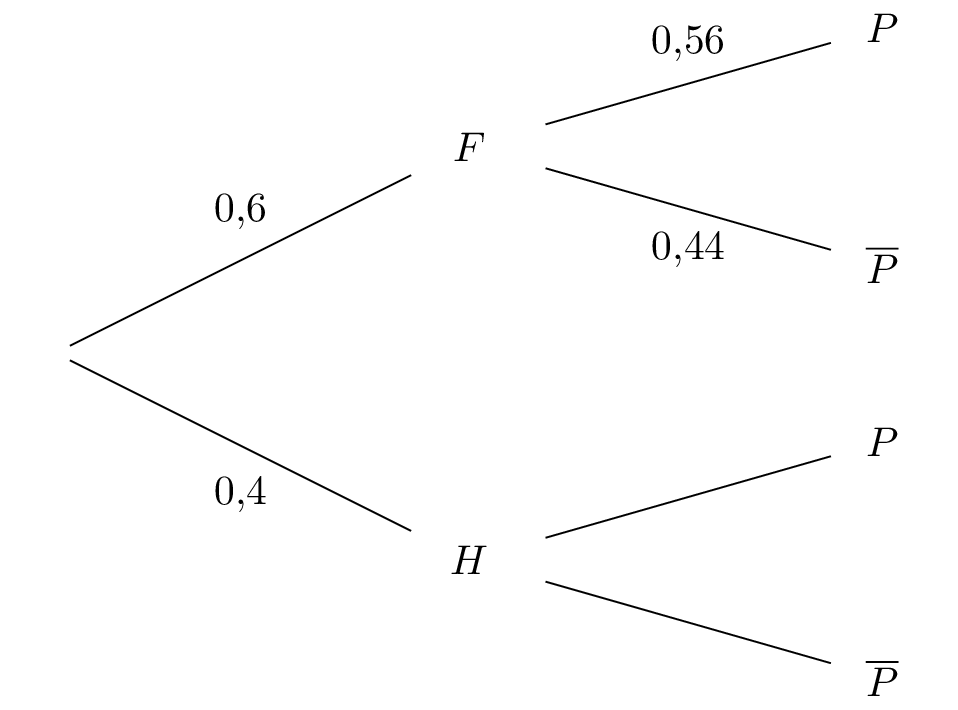
D'après une enquête menée auprès d'une population, on a constaté que :
- de la population sont des femmes ;
- des femmes travaillent à temps partiel ;
- de la population travaillent à temps partiel.
On interroge une personne dans la population.
Elle affirme qu'elle travaille à temps partiel.
Quelle est la probabilité que cette personne soit un homme ?
- de la population sont des femmes ;
- des femmes travaillent à temps partiel ;
- de la population travaillent à temps partiel.
Elle affirme qu'elle travaille à temps partiel.
Quelle est la probabilité que cette personne soit un homme ?
Correction
On note :
l'événement « la personne interrogée est une femme » ;
l'événement « la personne interrogée est un homme » ;
l'événement &laqup; la personne interrogée travaille à temps partiel » ;
l'événement « la personne interrogée ne travaille pas à temps partiel »
On regroupe les données du texte dans un arbre pondéré :
On cherche à déterminer la probabilité que la personne interrogée soit un homme, c'est à dire :
D'après le texte, .
Les évènements et forment une partition de l'univers.
D'après la formule des probabilités totales :
On en déduit que donc que .
Donc que :
La réponse est donc :
l'événement « la personne interrogée est une femme » ;
l'événement « la personne interrogée est un homme » ;
l'événement &laqup; la personne interrogée travaille à temps partiel » ;
l'événement « la personne interrogée ne travaille pas à temps partiel »
On regroupe les données du texte dans un arbre pondéré :

On cherche à déterminer la probabilité que la personne interrogée soit un homme, c'est à dire :
D'après le texte, .
Les évènements et forment une partition de l'univers.
D'après la formule des probabilités totales :
On en déduit que donc que .
Donc que :
La réponse est donc :