Les nombres complexes

Exploiter géométriquement l'affixe d'un vecteur - Exercice 1

5 min
10
Le plan est rapporté à un repère orthonormal direct (O;u⃗;v⃗)\left(O;\vec{u} ;\vec{v} \right)
Question 1

Soient les points AA, BB, CC et DD d'affixes respectives zA=−4−3iz_{A} =-4-3i , zB=3−2iz_{B} =3-2i , zC=4+5iz_{C} =4+5i et zD=−3+4iz_{D} =-3+4i. Quelle est la nature du quadrilatère 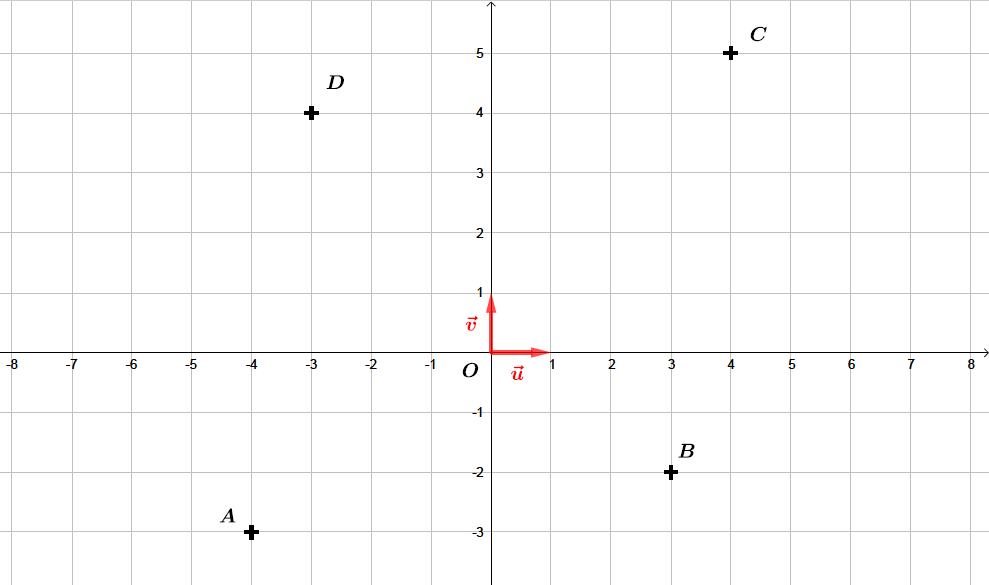ABCDABCD?

Correction
  • Si zAz_{A} et zBz_{B} sont les affixes respectives des points AA et BB dans un repère orthonormé, alors l'affixe du vecteur AB⃗\vec{AB} est égale à zAB⃗=zB−zAz_{\vec{AB} }=z_{B}-z_{A}.
  • La partie réelle de l'affixe d'un point se place sur l'axe des abscisses et la partie imaginaire de l'affixe d'un point se place sur l'axe des ordonnées.
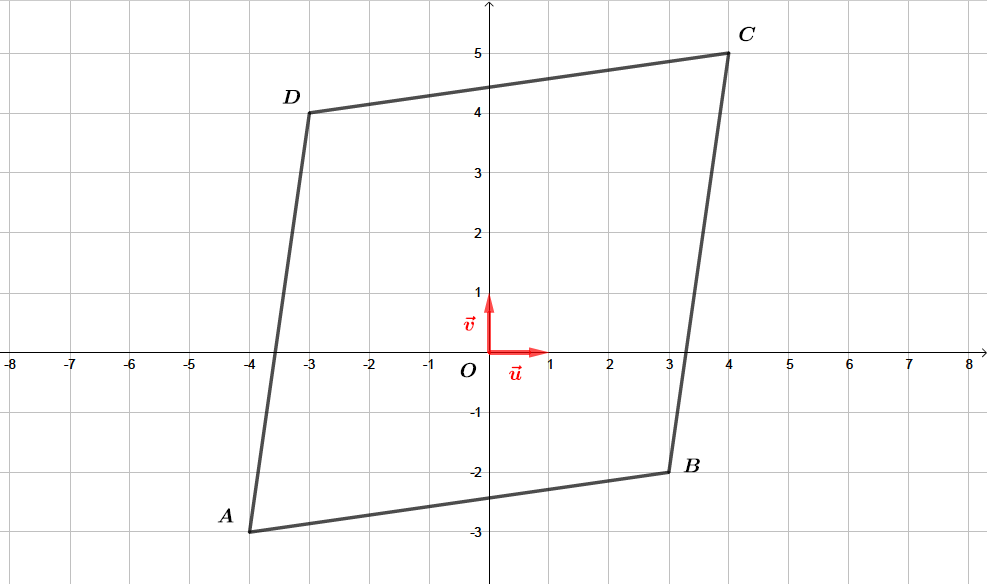
En plaçant les 44 affixes sur un repère, on conjecture que le quadrilatère ABCDABCD est un parallélogramme.
Montrons alors que zDC→=zAB→z_{\overrightarrow{DC} }=z_{\overrightarrow{AB} }.
D'une part :
zDC→=zC−zDz_{\overrightarrow{DC} }=z_{C}-z_{D}
zDC→=4+5i−(−3+4i)z_{\overrightarrow{DC} }=4+5i-\left(-3+4i\right)
zDC→=4+5i+3−4iz_{\overrightarrow{DC} }=4+5i+3-4i
zDC→=7+iz_{\overrightarrow{DC} }=7+i

D'autre part :
zAB→=zB−zAz_{\overrightarrow{AB} }=z_{B}-z_{A}
zAB→=3−2i−(−4−3i)z_{\overrightarrow{AB} }=3-2i-\left(-4-3i\right)
zAB→=3−2i+4+3iz_{\overrightarrow{AB} }=3-2i+4+3i
zAB→=7+iz_{\overrightarrow{AB} }=7+i

Nous avons bien zDC→=zAB→z_{\overrightarrow{DC} }=z_{\overrightarrow{AB} }. il en résulte que le quadrilatère ABCDABCD est un parallélogramme.