Les nombres complexes
Exercice 1 - Exercice 1
1 min
0
Pour chacune des propositions suivantes, dire si elle est vraie ou fausse en justifiant la réponse.
Le plan complexe est muni d'un repère orthonormal direct .
Le plan complexe est muni d'un repère orthonormal direct .
Question 1
Soit .
Proposition « est un imaginaire pur » .
Proposition « est un imaginaire pur » .
Correction
La proposition est fausse.
Commençons par donner la forme exponentielle de .
Pour cela , nous devons calculer le module et l'argument de .
Nous allons donner le résultat directement. Si vous rencontrez des difficultés reportez-vous à la fiche d'exercice.
Ainsi : et
Il vient alors que : l'écriture exponentielle de est
On en déduit que :
car
car :
(on a simplifié)
Maintenant on donne une mesure principale de .
Ainsi
Il vient alors que :
. Or
Ainsi :
Il en résulte que est un réel.
Commençons par donner la forme exponentielle de .
Pour cela , nous devons calculer le module et l'argument de .
Nous allons donner le résultat directement. Si vous rencontrez des difficultés reportez-vous à la fiche d'exercice.
Ainsi : et
Il vient alors que : l'écriture exponentielle de est
On en déduit que :
car
car :
(on a simplifié)
Maintenant on donne une mesure principale de .
Ainsi
Il vient alors que :
. Or
Ainsi :
Il en résulte que est un réel.
Question 2
Soit l'ensemble des points d'affixe telle que .
Proposition : « est une droite parallèle à l'axe des imaginaires purs ».
Proposition : « est une droite parallèle à l'axe des imaginaires purs ».
Correction
La proposition est fausse.
On définit les points et du plan complexe d'affixes et alors :
équivaut successivement à :
L'ensemble des points est donc la médiatrice du segment .
Lorsque nous plaçons les points et dans le plan complexe, on vérifie facilement que la médiatrice du segment est parallèle à l'axe des abscisses.
Géométriquement, un module est une distance
On définit les points et du plan complexe d'affixes et alors :
équivaut successivement à :
L'ensemble des points est donc la médiatrice du segment .
Lorsque nous plaçons les points et dans le plan complexe, on vérifie facilement que la médiatrice du segment est parallèle à l'axe des abscisses.
Question 3
Soit l'ensemble des points d'affixe telle que .
Proposition : « est le cercle dont l'écriture cartésienne est : » .
Proposition : « est le cercle dont l'écriture cartésienne est : » .
Correction
La proposition est Vraie.
On définit le point du plan complexe d'affixe alors :
équivaut successivement à :
L'ensemble des points est donc le cercle de centre , d'affixe , et de rayon .
Il en résulte que l'équation cartésienne du cercle est alors :
Un cercle de centre , d'affixe ,et de rayon a comme équation cartésienne
On commence par calculer On définit le point du plan complexe d'affixe alors :
équivaut successivement à :
L'ensemble des points est donc le cercle de centre , d'affixe , et de rayon .
Il en résulte que l'équation cartésienne du cercle est alors :
Question 4
Soient le point d'affixe et le point d'affixe .
Proposition : « le triangle est rectangle isocèle » .
Proposition : « le triangle est rectangle isocèle » .
Correction
La proposition est fausse.
Dans un premier temps, il faut placer les points sur le plan complexe.
On conjecture ainsi que le triangle serait rectangle en .
Il y a plusieurs manières de répondre à la question.
Méthode 1
En calculant les mesures des 3 cotés et en appliquant la réciproque du théorème de Pythagore.
Or : .
Le triangle n'est donc ni rectangle ni isocèle.
Méthode 2
On calcule le rapport : . (nous mettons à la fois au numérateur et au dénominateur car le triangle serait rectangle en ).
Il faudra ensuite obtenir un imaginaire pur en résultat algébrique.
En effet, si le résultat est un imaginaire pur alors son argument est égale à .
Et si alors .
Autrement dit le triangle serait rectangle en .
Ainsi : le point d'affixe et le point d'affixe .
On multiplie par le conjugué du dénominateur au numérateur et dénominateur, il vient :
, ce n'est donc pas un imaginaire pur.
Le triangle n'est donc pas rectangle.
Dans un premier temps, il faut placer les points sur le plan complexe.
On conjecture ainsi que le triangle serait rectangle en .
Il y a plusieurs manières de répondre à la question.
Méthode 1
En calculant les mesures des 3 cotés et en appliquant la réciproque du théorème de Pythagore.
Or : .
Le triangle n'est donc ni rectangle ni isocèle.
Méthode 2
On calcule le rapport : . (nous mettons à la fois au numérateur et au dénominateur car le triangle serait rectangle en ).
Il faudra ensuite obtenir un imaginaire pur en résultat algébrique.
En effet, si le résultat est un imaginaire pur alors son argument est égale à .
Et si alors .
Autrement dit le triangle serait rectangle en .
Ainsi : le point d'affixe et le point d'affixe .
On multiplie par le conjugué du dénominateur au numérateur et dénominateur, il vient :
, ce n'est donc pas un imaginaire pur.
Le triangle n'est donc pas rectangle.
Question 5
On considère les points et d'affixes respectifs , , et .
Proposition : « est un parallélogramme » .
Proposition : « est un parallélogramme » .
Correction
La proposition est vraie.
Il faut calculer les vecteurs et puis vérifiez s'ils sont bien égaux.
Ainsi : donc est un parallélogramme.
Il faut calculer les vecteurs et puis vérifiez s'ils sont bien égaux.
Ainsi : donc est un parallélogramme.
Question 6
Soient et .
Proposition : « ».
Proposition : « ».
Correction
La proposition est vraie.
équivaut successivement à :
(on utilise le rappel)
(on utilise à nouveau le rappel)
(on utilise le rappel)
(on utilise à nouveau le rappel)
Question 7
A tout nombre complexe , on associe le nombre complexe défini par : .
Proposition : « L'ensemble des points d'affixe tels que est un cercle » .
Proposition : « L'ensemble des points d'affixe tels que est un cercle » .
Correction
La proposition est fausse.
équivaut successivement à :
Or
On définit les points et du plan complexe d'affixes et alors :
équivaut successivement à :
L'ensemble des points est donc la médiatrice du segment .
équivaut successivement à :
Or
On définit les points et du plan complexe d'affixes et alors :
équivaut successivement à :
L'ensemble des points est donc la médiatrice du segment .
Question 8
On considère les points et d'affixes respectifs , , et .
Proposition : « les points sont sur le cercle de centre » .
Proposition : « les points sont sur le cercle de centre » .
Correction
La proposition est fausse.
Si les points sont sur le cercle de centre alors les distances , et seront égales.
Nous remarquons que les trois distances ne sont pas égales donc les points ne sont pas sur le cercle de centre .
Si les points sont sur le cercle de centre alors les distances , et seront égales.
Nous remarquons que les trois distances ne sont pas égales donc les points ne sont pas sur le cercle de centre .
Question 9
On désigne par le complexe : .
On pose : .
Proposition : « ».
On pose : .
Proposition : « ».
Correction
La proposition est fausse.
équivaut successivement à :
On développe d'une part :
On obtient alors :
Donc :
équivaut successivement à :
On développe d'une part :
On obtient alors :
Donc :
Question 10
Soient et l'équation .
Proposition : « admet deux racines complexes conjuguées » .
Proposition : « admet deux racines complexes conjuguées » .
Correction
La proposition est vraie.
Il s'agit d'une équation du second degré.
Nous allons utiliser le discriminant.
, il existe donc deux racines complexes conjuguées.
Il s'agit d'une équation du second degré.
Nous allons utiliser le discriminant.
, il existe donc deux racines complexes conjuguées.
Question 11
Soient et l'équation .
Proposition : « admet une solution imaginaire pure ».
Proposition : « admet une solution imaginaire pure ».
Correction
La proposition est fausse.
Dans le cas où nous avons une équation avec du et du , il faut poser et
équivaut successivement à :
Par identification, on a :
Finalement la solution de l'équation est alors et n'est pas une solution imaginaire pure.
Dans le cas où nous avons une équation avec du et du , il faut poser et
équivaut successivement à :
Par identification, on a :
Finalement la solution de l'équation est alors et n'est pas une solution imaginaire pure.
Question 12
Pour tout entier naturel , on note le point d'affixe défini par et .
On définit la suite par pour tout entier naturel .
Proposition : « la suite est convergente ».
On définit la suite par pour tout entier naturel .
Proposition : « la suite est convergente ».
Correction
La proposition est fausse.
Nous allons dans un premier temps montrer que la suite est une suite géométrique.
On sait que
D'où :
Or , donc
On calcule
Il en résulte que est une suite géométrique de raison
Calculons le premier terme de la suite.
, or donc
Nous pouvons maintenant exprimer en fonction de . Il vient alors que :
Calculons maintenant .
d'où .
La suite est divergente.
Nous allons dans un premier temps montrer que la suite est une suite géométrique.
On sait que
D'où :
Or , donc
On calcule
Il en résulte que est une suite géométrique de raison
Calculons le premier terme de la suite.
, or donc
Nous pouvons maintenant exprimer en fonction de . Il vient alors que :
Calculons maintenant .
d'où .
La suite est divergente.
Question 13
Soit
Proposition : « L'ensemble des points du plan d'affixe z tels que est une droite » .
Proposition : « L'ensemble des points du plan d'affixe z tels que est une droite » .
Correction
La proposition est fausse.
Soit le point d'affixe
équivaut successivement à :
est donc un point de la demi-droite passant par et faisant l'angle avec le vecteur (privée du point )
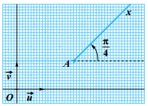
Soit le point d'affixe
équivaut successivement à :
est donc un point de la demi-droite passant par et faisant l'angle avec le vecteur (privée du point )

Question 14
Soit est -il vrai que :
Correction
La proposition est fausse.
Comme alors :
équivaut successivement à :
. Or , d'où :
équivaut successivement à :
. Or , d'où :
Question 15
Correction
La proposition est fausse.
Question 16
La solution de l’équation est
Correction
La proposition est vraie.