Les lois continues

QCM - Exercice 1

20 min
35
Cet exercice est un questionnaire à choix multiples (Q.C.M.). Pour chacune des questions, une seule des quatre réponses est exacte.
Question 1
On étudie la production d’une usine qui fabrique des bonbons, conditionnés en sachets. On choisit un sachet au hasard dans la production journalière. La masse de ce sachet, exprimée en gramme, est modélisée par une variable aléatoire XX qui suit une loi normale d’espérance μ=175\mu=175. De plus, une observation statistique a montré que 22% des sachets ont une masse inférieure ou égale à 170170 g, ce qui se traduit dans le modèle considéré par : P(X≤170)=0,02P\left(X\le 170\right)=0,02

Quelle est la probabilité, arrondie au centième, de l’évènement « la masse du sachet est comprise entre 170170 et 180180 grammes »?
  • 0,040,04
  • 0,960,96
  • 0,980,98
  • On ne peut pas répondre car il manque des données.

Correction
La bonne réponse est b.
On sait que P(X≤170)=0,02P\left(X\le 170\right)=0,02. De plus, par symétrie par rapport à l’espérance μ=175\mu=175, il en résulte alors que P(X≥180)=0,02P\left(X\ge 180\right)=0,02
Ainsi :
P(170≤X≤180)=1−P(X≤170)−P(X≥180)P\left(170\le X\le 180\right)=1-P\left(X\le 170\right)-P\left(X\ge 180\right)
D'où :
P(170≤X≤180)=1−0,02−0,02P\left(170\le X\le 180\right)=1-0,02-0,02
Finalement :
P(170≤X≤180)=0,96P\left(170\le X\le 180\right)=0,96
Question 2
Les différents bonbons présents dans les sachets sont tous enrobés d’une couche de cire comestible. Ce procédé, qui déforme certains bonbons, est effectué par deux machines AA et BB. Lorsqu’il est produit par la machine AA, la probabilité qu’un bonbon prélevé aléatoirement soit déformé est égale à 0,050,05.

Sur un échantillon aléatoire de 5050 bonbons issus de la machine AA, quelle est la probabilité, arrondie au centième, qu’au moins 22 bonbons soient déformés?
  • 0,720,72
  • 0,280,28
  • 0,540,54
  • On ne peut pas répondre car il manque des données.

Correction
La bonne réponse est a.
A chaque tirage la probabilité de tirer bonbon déformé est de 0,050,05
On est donc en présence d'un schéma de Bernoulli :
On appelle succès "tirer un bonbon déformé" avec la probabilité p=0,05p=0,05
On appelle échec "tirer un bonbon non déformé" avec la probabilité 1−p=0,951-p=0,95
On répète 5050 fois de suite cette expérience de façon indépendante.
XX est la variable aléatoire qui associe le nombre bonbons déformés.
XX suit la loi binomiale de paramètre n=50n=50 et p=0,05p=0,05
On note alors X∼B(50;0,05)X \sim B\left(50;0,05 \right)

Nous devons calculer P(X≥2)P\left(X\ge 2\right)
Or : P(X≥2)=1−P(X≤1)P\left(X\ge 2\right)=1-P\left(X\le 1\right)
P(X≥2)=1−P(X=1)−P(X=0)P\left(X\ge 2\right)=1-P\left(X=1\right)-P\left(X=0\right). D'après la calculatrice, on obtient :
P(X≥2)=0,72P\left(X\ge 2\right)=0,72
Question 3
La machine AA produit un tiers des bonbons de l’usine. Le reste de la production est assuré par la machine BB. Lorsqu’il est produit par la machine BB, la probabilité qu’un bonbon prélevé aléatoirement soit déformé est égale à 0,020,02. Dans un test de contrôle, on prélève au hasard un bonbon dans l’ensemble de la production. Celui-ci est déformé.

Quelle est la probabilité, arrondie au centième, qu’il soit produit par la machine BB?
  • 0,020,02
  • 0,670,67
  • 0,440,44
  • 0,010,01

Correction
La bonne réponse est c.
Nous allons commencer par traduire l'énoncé à l'aide d'un arbre pondéré, en utilisant les données de la question 22 et 33.
  • On note AA l'évènement : produit par la machine AA.
  • On note BB l'évènement : produit par la machine BB.
  • On note DD l'évènement : le bonbon est déformé.


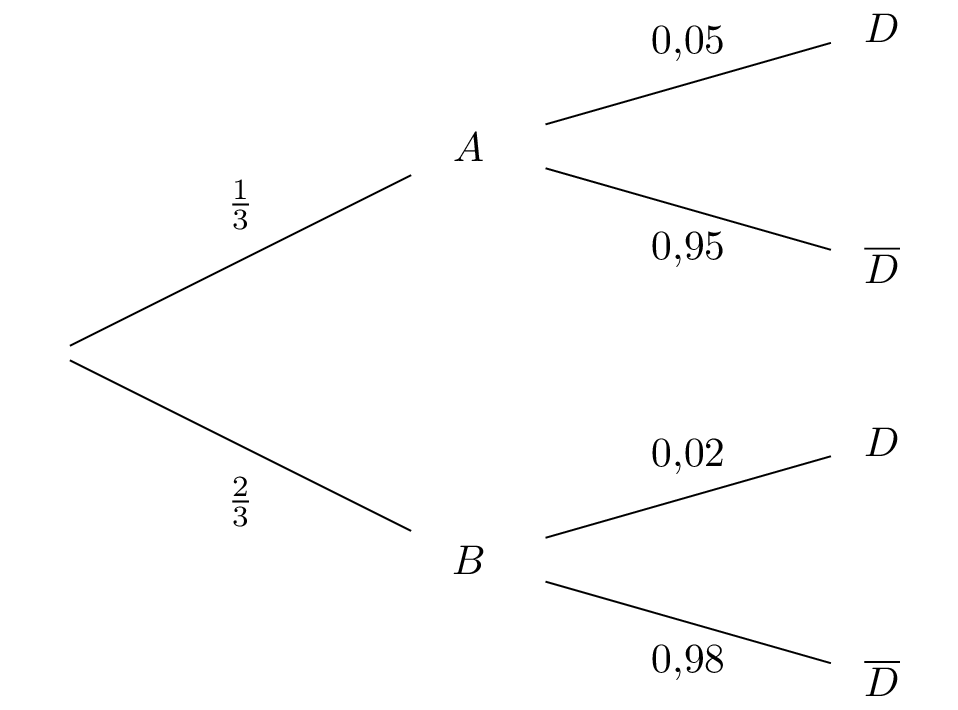
    • On souhaite calculer la probabilité conditionnelle :
    PD(B)=P(B∩D)P(D)P_{D} \left(B\right)=\frac{P\left(B\cap D\right)}{P\left(D\right)} équivaut successivement à :
    PD(B)=P(B∩D)P(A∩D)+P(B∩D)P_{D} \left(B\right)=\frac{P\left(B\cap D\right)}{P\left(A\cap D\right)+P\left(B\cap D\right)}
    PD(B)=P(B)×PB(D)P(A)×PA(D)+P(B)×PB(D)P_{D} \left(B\right)=\frac{P\left(B\right)\times P_{B} \left(D\right)}{P\left(A\right)\times P_{A} \left(D\right)+P\left(B\right)\times P_{B} \left(D\right)}
    PD(B)=23×0,0213×0,05+23×0,02P_{D} \left(B\right)=\frac{\frac{2}{3}\times 0,02}{\frac{1}{3}\times 0,05+\frac{2}{3}\times 0,02}
    PD(B)=49P_{D} \left(B\right)=\frac{4}{9}
    PD(B)≈0,44P_{D} \left(B\right)\approx0,44
    Question 4
    La durée de vie de fonctionnement, exprimée en jour, d’une machine servant à l’enrobage, est modélisée par une variable aléatoire YY qui suit la loi exponentielle dont l’espérance est égale à 500500 jours.

    Quelle est la probabilité, arrondie au centième, que la durée de fonctionnement de la machine soit inférieure ou égale à 300300 jours?
    • 0,450,45
    • 11
    • 0,550,55
    • On ne peut pas répondre car il manque des données.

    Correction
    La bonne réponse est a.
    Si XX suit une loi exponentielle de paramètre λ\lambda alors son espérance mathématique vaut E(X)=1λE\left(X\right)=\frac{1}{\lambda }
    YY qui suit la loi exponentielle dont l’espérance est égale à 500500 jours. Ainsi : E(Y)=500E\left(Y\right)=500.
    Il vient alors que : 1λ=500\frac{1}{\lambda }=500 donc
    λ=1500\lambda=\frac{1}{500}

    La fonction de densité de probabilité de la loi exponentielle sur [0;+∞[\left[0;+\infty \right[ est f(x)=λe−λxf\left(x\right)=\lambda e^{-\lambda x} où λ\lambda est un réel positif.
    • P(a≤X≤b)=∫abλe−λxdx=[−e−λx]ab=e−λa−e−λbP\left(a\le X\le b\right)=\int _{a}^{b}\lambda e^{-\lambda x} dx=\left[-e^{-\lambda x} \right] _{a}^{b} =e^{-\lambda a} -e^{-\lambda b}
    • P(X≤a)=P(0≤X≤a)=∫0aλe−λxdx=[−e−λx]0a=1−e−λaP\left(X\le a\right)=P\left(0\le X\le a\right)=\int _{0}^{a}\lambda e^{-\lambda x} dx=\left[-e^{-\lambda x} \right] _{0}^{a} =1-e^{-\lambda a}
    • P(X≥a)=1−P(X≤a)=1−(1−e−λa)=e−λaP\left(X\ge a\right)=1-P\left(X\le a\right)=1-\left(1-e^{-\lambda a} \right)=e^{-\lambda a}
    P(Y≤300)=P(0≤Y≤300)P\left(Y\le 300\right)=P\left(0\le Y\le 300\right)
    Calculons : P(0≤Y≤300)P\left(0\le Y\le 300\right)
    P(0≤Y≤300)=∫0300λe−λxdxP\left(0\le Y\le 300\right)=\int _{0}^{300}\lambda e^{-\lambda x} dx équivaut successivement à
    P(0≤Y≤300)=∫031500e−1500xdxP\left(0\le Y\le 300\right)=\int _{0}^{3}\frac{1}{500}e^{-\frac{1}{500}x} dx
    P(0≤Y≤300)=[−e−1500x]0300P\left(0\le Y\le 300\right)=\left[-e^{-\frac{1}{500}x} \right]_{0}^{300}
    P(0≤Y≤300)=e−1500×0−e−1500×300P\left(0\le Y\le 300\right)=e^{-\frac{1}{500}\times 0} -e^{-\frac{1}{500}\times 300}
    P(0≤Y≤300)=1−e−35P\left(0\le Y\le 300\right)=1 -e^{-\frac{3}{5}}
    Ainsi :
    P(0≤Y≤300)≈0,45P\left(0\le Y\le 300\right)\approx 0,45
    Question 5
    L’entreprise souhaite estimer la proportion de personnes de plus de 2020 ans parmi ses clients, au niveau de confiance de 9595%, avec un intervalle d’amplitude inférieure à 0,050,05. Elle interroge pour cela un échantillon aléatoire de clients.

    Quel est le nombre minimal de clients à interroger?
    • 4040
    • 400400
    • 16001600
    • 2020

    Correction
    La bonne réponse est c.
    Au niveau de confiance de 9595%, l'amplitude pour un intervalle de confiance est donnée par la formule 2n\frac{2}{\sqrt{n} } .
    Nous devons résoudre l'inéquation 2n≤0,05\frac{2}{\sqrt{n} } \le 0,05.
    Ainsi :
    2n≤0,05\frac{2}{\sqrt{n} } \le 0,05 équivaut successivement à
    n2≥10,05\frac{\sqrt{n} }{2} \ge \frac{1}{0,05}
    n≥20,05\sqrt{n} \ge \frac{2}{0,05}
    n≥(20,05)2n\ge \left(\frac{2}{0,05} \right)^{2}
    Finalement :
    n≥1600n\ge 1600

    Il faudrait, au minimum, interroger 16001600 clients pour obtenir un intervalle de confiance à 9595% de longueur inférieur ou égale à 0,050,05.