Les lois continues

Exercice 4 - Exercice 1

1 min
0
Cet exercice est un questionnaire à choix multiples.
Pour chaque question posée, une seule des réponses proposées est exacte.
On demande bien sûr de justifier.
Question 1

On choisit au hasard un nombre xx dans l'intervalle [−3;2]\left[-3;2\right].
La probabilité qu'il appartienne à l'intervalle [−1;2]\left[-1;2\right] est :
  • 35\frac{3}{5}
  • 13\frac{1}{3}
  • 25\frac{2}{5}
  • 12\frac{1}{2}

Correction
La proposition correcte est la proposition a.
On suppose que la probabilité de choisir un nombre xx dans l'intervalle [−3;2]\left[-3;2\right] suit une loi uniformément répartie.
La fonction de densité de probabilité de la loi uniforme sur [−3;2]\left[-3;2\right] est f(x)=12−(−3)=15f\left(x\right)=\frac{1}{2-\left(-3\right)} =\frac{1}{5} .
P(−1≤X≤2)=∫−12f(x)dxP\left(-1\le X\le 2\right)=\int _{-1}^{2}f\left(x\right)dx
P(−1≤X≤2)=[15x]−12P\left(-1\le X\le 2\right)=\left[\frac{1}{5} x\right]_{-1}^{2}
P(−1≤X≤2)=(15×2−19×(−1))P\left(-1\le X\le 2\right)=\left(\frac{1}{5} \times 2-\frac{1}{9} \times \left(-1\right)\right)
P(−1≤X≤2)=35P\left(-1\le X\le 2\right)=\frac{3}{5}
Soit XX une variable aléatoire suivant la loi uniforme sur l'intervalle[a;b]\left[a;b\right] alors : P(c≤X≤d)=d−cb−aP\left(c\le X\le d\right)=\frac{d-c}{b-a} .
Cette formule permet de calculer rapidement les probabilités issues d'une loi uniforme. Voyez avec votre prof s'il la valide en DS. Vous aurez ainsi , ci-dessus le corrigé détaillé de la question et ci-dessous le corrigé sans passer par le calcul de l'intégrale. A vous de choisir :)
On a :
P(−1≤X≤2)=2−(−1)−3−2P\left(-1\le X\le 2\right)=\frac{2-\left(-1\right)}{-3-2}
P(−1≤X≤2)=35P\left(-1\le X\le 2\right)=\frac{3}{5}
Question 2

Soit XX une variable aléatoire qui suit la loi normale de moyenne 22 et d'écart-type σ\sigma .
On suppose que P(−2≤X≤6)≈0,95P\left(-2\le X\le 6\right)\approx 0,95 .
Alors :
  • σ=1\sigma =1
  • σ=2\sigma =2
  • σ=3\sigma =3
  • σ=4\sigma =4

Correction
La proposition correcte est la proposition b.
Si XX suit une loi normale de paramètre μ\mu et σ\sigma alors :
P(μ−σ≤X≤μ+σ)=0,683P\left(\mu -\sigma \le X\le \mu +\sigma \right)=0,683
P(μ−2σ≤X≤μ+2σ)=0,954P\left(\mu -2\sigma \le X\le \mu +2\sigma \right)=0,954
P(μ−3σ≤X≤μ+3σ)=0,997P\left(\mu -3\sigma \le X\le \mu +3\sigma \right)=0,997
Nous avons alors que : P(2−2σ≤X≤2+2σ)=0,954P\left(2 -2\sigma \le X\le 2 +2\sigma \right)=0,954 et nous voulons que P(−2≤X≤6)≈0,95P\left(-2\le X\le 6\right)\approx 0,95
Par identification, nous avons alors :
2−2σ=−22 -2\sigma =-2 et 2+2σ=62 +2\sigma =6
On trouvera alors
σ=2\sigma=2
Question 3

Soit XX une variable aléatoire qui suit la loi normale centrée réduite.
On a P(X≤2)≈0,977P\left(X\le 2\right)\approx 0,977, alors :
  • P(0≤X≤2)≈0,333P\left(0\le X\le 2\right)\approx 0,333
  • P(0≤X≤2)≈0,477P\left(0\le X\le 2\right)\approx 0,477
  • P(0≤X≤2)≈0,217P\left(0\le X\le 2\right)\approx 0,217
  • P(0≤X≤2)≈0,123P\left(0\le X\le 2\right)\approx 0,123

Correction
La proposition correcte est la proposition b.
P(X≤2)=P(X≤0)+P(0≤X≤2)P\left(X\le 2\right)=P\left(X\le 0\right)+P\left(0\le X\le 2\right)
Or P(X≤0)=12P\left(X\le 0\right)=\frac{1}{2} .
Ainsi : P(X≤2)−P(X≤0)=P(0≤X≤2)P\left(X\le 2\right)-P\left(X\le 0\right)=P\left(0\le X\le 2\right)
D'où :
P(0≤X≤2)≈0,477P\left(0\le X\le 2\right)\approx 0,477
Question 4

Une certaine espèce de cactus a une durée de vie moyenne de 100100 ans et on convient de modéliser sa durée de vie en années par une variable aléatoire XX suivant une loi exponentielle.
La probabilité que le cactus vive au moins 135135 ans vaut :
  • e−1,35e^{-1,35}
  • 1−e−1,351-e^{-1,35}
  • e0.01−e−1,35e^{0.01} -e^{-1,35}
  • e−1,35−e0.01e^{-1,35} -e^{0.01}

Correction
La proposition correcte est la proposition a.
La fonction de densité de probabilité de la loi exponentielle sur [0;+∞[\left[0;+\infty \right[ est f(x)=λe−λxf\left(x\right)=\lambda e^{-\lambda x} où λ\lambda est un réel positif.
  • P(a≤X≤b)=∫abλe−λxdx=[−e−λx]ab=e−λa−e−λbP\left(a\le X\le b\right)=\int _{a}^{b}\lambda e^{-\lambda x} dx=\left[-e^{-\lambda x} \right] _{a}^{b} =e^{-\lambda a} -e^{-\lambda b}
  • P(X≤a)=P(0≤X≤a)=∫0aλe−λxdx=[−e−λx]0a=1−e−λaP\left(X\le a\right)=P\left(0\le X\le a\right)=\int _{0}^{a}\lambda e^{-\lambda x} dx=\left[-e^{-\lambda x} \right] _{0}^{a} =1-e^{-\lambda a}
  • P(X≥a)=1−P(X≤a)=1−(1−e−λa)=e−λaP\left(X\ge a\right)=1-P\left(X\le a\right)=1-\left(1-e^{-\lambda a} \right)=e^{-\lambda a}
On rappelle également que l'espérance d'une loi exponentielle vaut 1λ\frac{1}{\lambda } .
Il en résulte alors que 1λ=100\frac{1}{\lambda } =100 d'où λ=0,01\lambda =0,01.
Nous devons ensuite calculer :
P(X≥135)=1−P(X≤135)=1−(1−e−0.01×135)=e−1,35P\left(X\ge 135\right)=1-P\left(X\le 135\right)=1-\left(1-e^{-0.01\times 135} \right)=e^{-1,35}
Question 5

Il peut les vendre sur le marché à condition que 376≤X≤424376\le X\le 424
Quelle est la probabilité qu'une botte de carottes prise au hasard ne soit pas vendue ?
  • 0,9970,997
  • 0,6840,684
  • 0,9540,954
  • 0,0030,003

Correction
La proposition correcte est la proposition d.
Notons AA l'évènement « une botte de carottes prise au hasard ne soit pas vendue ».
p(A)=1−p(376≤X≤424)p\left(A\right)=1-p\left(376\le X\le 424\right)
Or p(376≤X≤424)=P(μ−3σ≤X≤μ+3σ)=0,997p\left(376\le X\le 424\right)=P\left(\mu -3\sigma \le X\le \mu +3\sigma \right)=0,997
Ainsi :
p(A)=1−0.997=0,003p\left(A\right)=1-0.997=0,003
Question 6

La représentation graphique de la fonction ff, donné ci-dessous, représente-t-elle une fonction de densité sur l'intervalle [−12;52]\left[-\frac{1}{2} ;\frac{5}{2} \right] ?

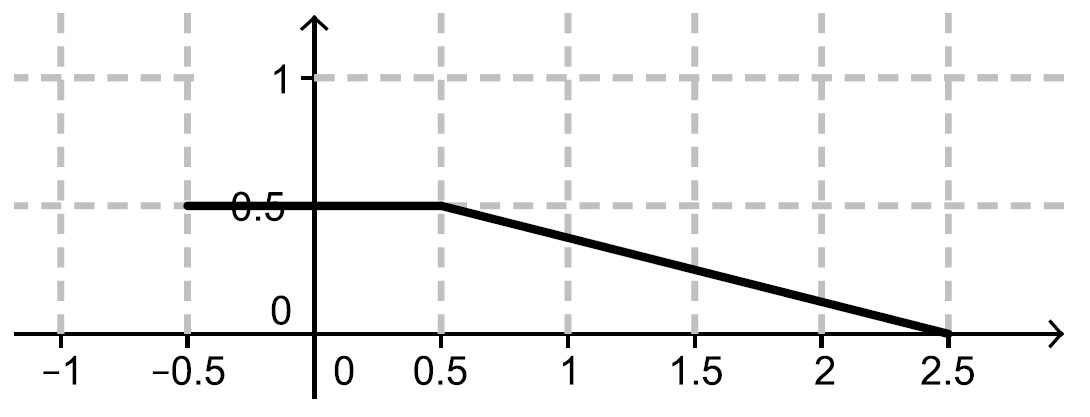
  • Vrai
  • Faux

Correction
La proposition correcte est la proposition a.
∫−1252f(x)dx=∫−1212f(x)dx+∫1252f(x)dx\int _{-\frac{1}{2} }^{\frac{5}{2} }f\left(x\right)dx =\int _{-\frac{1}{2} }^{\frac{1}{2} }f\left(x\right)dx +\int _{\frac{1}{2} }^{\frac{5}{2} }f\left(x\right)dx (D'après la relation de Chasles)
Sur l'intervalle [−12;12]\left[-\frac{1}{2} ;\frac{1}{2} \right], la fonction ff s'écrit f(x)=12f\left(x\right)=\frac{1}{2}
Sur l'intervalle [−12;12]\left[-\frac{1}{2} ;\frac{1}{2} \right], la fonction ff s'écrit f(x)=−14x+58f\left(x\right)=-\frac{1}{4} x+\frac{5}{8} ( on note par exemple le point A(12;12)A\left(\frac{1}{2} ;\frac{1}{2} \right) et B(52;0)B\left(\frac{5}{2} ;0\right) . On calcule l'équation de la droite (AB)\left(AB\right) qui donnera f(x)=−14x+58f\left(x\right)=-\frac{1}{4} x+\frac{5}{8} )
Il en résulte que
∫−1252f(x)dx=∫−121212dx+∫1252(−14x+58)dx\int _{-\frac{1}{2} }^{\frac{5}{2} }f\left(x\right)dx =\int _{-\frac{1}{2} }^{\frac{1}{2} }\frac{1}{2} dx +\int _{\frac{1}{2} }^{\frac{5}{2} }\left(-\frac{1}{4} x+\frac{5}{8} \right)dx
∫−1252f(x)dx=[12x]−1212+[−18x2+58x]1252\int _{-\frac{1}{2} }^{\frac{5}{2} }f\left(x\right)dx =\left[\frac{1}{2} x\right]_{-\frac{1}{2} }^{\frac{1}{2} } +\left[-\frac{1}{8} x^{2} +\frac{5}{8} x\right]_{\frac{1}{2} }^{\frac{5}{2} }
∫−1252f(x)dx=[12×12−12×(−12)]+[(−18×(52)2+58×52)−(−18×(12)2+58×12)]\int _{-\frac{1}{2} }^{\frac{5}{2} }f\left(x\right)dx =\left[\frac{1}{2} \times \frac{1}{2} -\frac{1}{2} \times \left(-\frac{1}{2} \right)\right]+\left[\left(-\frac{1}{8} \times \left(\frac{5}{2} \right)^{2} +\frac{5}{8} \times \frac{5}{2} \right)-\left(-\frac{1}{8} \times \left(\frac{1}{2} \right)^{2} +\frac{5}{8} \times \frac{1}{2} \right)\right]
∫−1252f(x)dx=1.\int _{-\frac{1}{2} }^{\frac{5}{2} }f\left(x\right)dx =1.
De plus sur l'intervalle [−12;52]\left[-\frac{1}{2} ;\frac{5}{2} \right], ff est continue et positive .
Il en résulte que ff est une fonction de densité sur l'intervalle [−12;52]\left[-\frac{1}{2} ;\frac{5}{2} \right].
Question 7

Soit mm un réel positif.
Soit XX une variable aléatoire de densité ff définie pour tout xx de [0;m]\left[0;m\right] par f(x)=12f\left(x\right)=\frac{1}{2} .
On sait que l'espérance de XX vaut 11.
La valeur de mm est alors égale à :
  • 00
  • 11
  • 22
  • 33

Correction
La proposition correcte est la proposition b.
L'espérance mathématique d'une variable aléatoire continue XX, de densité ff sur [a,b]\left[a,b\right] est E(X)=∫abxf(x)dxE\left(X\right)=\int _{a}^{b}xf\left(x\right)dx

Ainsi :
E(X)=∫0mxf(x)dxE\left(X\right)=\int _{0}^{m}xf\left(x\right)dx équivaut successivement à
E(X)=∫0mx×(12)dxE\left(X\right)=\int _{0}^{m}x\times \left(\frac{1}{2} \right)dx
Donc : E(X)=∫0m(12x)dxE\left(X\right)=\int _{0}^{m}\left(\frac{1}{2} x\right)dx .
Finalement,
E(X)=∫0m(12x)dxE\left(X\right)=\int _{0}^{m}\left(\frac{1}{2} x\right)dx équivaut successivement à
E(X)=[x2]0mE\left(X\right)=\left[x^{2} \right]_{0}^{m}
E(X)=(m2)−(0)E\left(X\right)=\left(m^{2} \right)-\left(0\right)
E(X)=m2E\left(X\right)=m^{2}
or E(X)=1E\left(X\right)=1 d'où m2=1m^{2} =1.
Donc soit m=1m=1 et m=−1m=-1.
Comme m≥0m\ge 0.
On ne retient que m=1m=1
Question 8

Si XX suit la loi normale N(μ;σ2)N\left(\mu ;\sigma ^{2} \right) d'espérance μ\mu et d'écart type σ\sigma , alors la variable centrée réduite associée à XX est :
  • X−μσ2\frac{X-\mu }{\sigma ^{2} }
  • X−μσ2X-\frac{\mu }{\sigma ^{2} }
  • X−μσ\frac{X-\mu }{\sigma }
  • X−μσX-\frac{\mu }{\sigma }

Correction
La proposition correcte est la proposition c.
Il s'agit d'une définition du cours.

Si une variable aléatoire XX suit une loi normale de paramètres μ\mu et σ\sigma notée N(μ;σ2)N\left(\mu;\sigma ^{2} \right), alors la variable aléatoire Z=X−μσZ=\frac{X-\mu }{\sigma} suit une loi normale centrée réduite N(0;1)N\left(0;1\right)
Question 9

Soit XX une variable aléatoire suivant la loi normale N(4;9)N\left(4;9\right). ZZ est une variable aléatoire suivant la loi normale centrée réduite.
Exprimer P(1≤X≤7)P\left(1\le X\le 7\right) sous la forme d'une probabilité impliquant uniquement la variable ZZ.
On a donc :
  • P(1≤X≤7)=P(−19≤Z≤19)P\left(1\le X\le 7\right)=P\left(-\frac{1}{9} \le Z\le \frac{1}{9} \right)
  • P(1≤X≤7)=P(−1≤Z≤1)P\left(1\le X\le 7\right)=P\left(-1\le Z\le 1\right)
  • P(1≤X≤7)=P(−2≤Z≤2)P\left(1\le X\le 7\right)=P\left(-2\le Z\le 2\right)
  • P(1≤X≤7)=P(−29≤Z≤29)P\left(1\le X\le 7\right)=P\left(-\frac{2}{9} \le Z\le \frac{2}{9} \right)

Correction
La proposition correcte est la proposition b.
XX suit la loi normale N(4;9)N\left(4;9\right) c'est à dire N(4;32)N\left(4;3^{2} \right)
On sait également que Z=X−43Z=\frac{X-4}{3} suit la loi normale centrée réduite .
Il vient alors que :
P(1≤X≤7)=P(1−4≤X−4≤7−4)P\left(1\le X\le 7\right)=P\left(1-4\le X-4\le 7-4\right)
P(1≤X≤7)=P(1−43≤X−43≤7−43)P\left(1\le X\le 7\right)=P\left(\frac{1-4}{3} \le \frac{X-4}{3} \le \frac{7-4}{3} \right)
P(1≤X≤7)=P(−1≤X−43≤1)P\left(1\le X\le 7\right)=P\left(-1\le \frac{X-4}{3} \le 1\right)
P(1≤X≤7)=P(−1≤Z≤1)P\left(1\le X\le 7\right)=P\left(-1\le Z\le 1\right)
car Z=X−43Z=\frac{X-4}{3}
Question 10

La variable aléatoire XX égale à la durée de vie d'un papillon suit une loi exponentielle.
On sait que la probabilité que cette durée de vie soit inférieure à deux jours est égale à 0,15 à 10−210^{-2} près.
Le paramètre λ\lambda de cette loi exponentielle vaut :
  • λ=ln⁡(0,85)2\lambda =\frac{\ln \left(0,85\right)}{2}
  • λ=ln⁡(0,85)−2\lambda =\frac{\ln \left(0,85\right)}{-2}
  • λ=ln⁡(2)0,85\lambda =\frac{\ln \left(2\right)}{0,85}
  • λ=ln⁡(0,15)−2\lambda =\frac{\ln \left(0,15\right)}{-2}

Correction
La proposition correcte est la proposition b.
La fonction de densité de probabilité de la loi exponentielle sur [0;+∞[\left[0;+\infty \right[ est f(x)=λe−λxf\left(x\right)=\lambda e^{-\lambda x} où λ\lambda est un réel positif.
  • P(a≤X≤b)=∫abλe−λxdx=[−e−λx]ab=e−λa−e−λbP\left(a\le X\le b\right)=\int _{a}^{b}\lambda e^{-\lambda x} dx=\left[-e^{-\lambda x} \right] _{a}^{b} =e^{-\lambda a} -e^{-\lambda b}
  • P(X≤a)=P(0≤X≤a)=∫0aλe−λxdx=[−e−λx]0a=1−e−λaP\left(X\le a\right)=P\left(0\le X\le a\right)=\int _{0}^{a}\lambda e^{-\lambda x} dx=\left[-e^{-\lambda x} \right] _{0}^{a} =1-e^{-\lambda a}
  • P(X≥a)=1−P(X≤a)=1−(1−e−λa)=e−λaP\left(X\ge a\right)=1-P\left(X\le a\right)=1-\left(1-e^{-\lambda a} \right)=e^{-\lambda a}
D'après l'énoncé, on a :
P(X≤2)=0,15P\left(X\le 2\right)=0,15 équivaut successivement à
1−e−2λ=0,151-e^{-2\lambda } =0,15
−e−2λ=−0,85-e^{-2\lambda } =-0,85
e−2λ=0,85e^{-2\lambda } =0,85
ln⁡(e−2λ)=ln⁡(0,85)\ln \left(e^{-2\lambda } \right)=\ln \left(0,85\right)
−2λ=ln⁡(0,85)-2\lambda =\ln \left(0,85\right)
λ=ln⁡(0,85)−2\lambda =\frac{\ln \left(0,85\right)}{-2}

Question 11

La durée de vie (exprimée en heures) d'un certain type de batteries est une variable aléatoire XX qui suit la loi exponentielle de paramètre λ=0,01\lambda =0,01.
La probabilité qu'une batterie fonctionne encore au bout de 800 heures sachant qu'elle fonctionnait encore au bout de 650650 heures est :
  • e−0,01×150e^{-0,01\times 150}
  • 1−e−0,01×1501-e^{-0,01\times 150}
  • e−0,01×150−1e^{-0,01\times 150} -1
  • e−0,01×800−e−0,01×650e^{-0,01\times 800} -e^{-0,01\times 650}

Correction
La proposition correcte est la proposition a.
La loi exponentielle est une loi sans vieillissement ou sans mémoire c'est-à-dire que : ∀t>0\forall t>0 et h>0h>0 on a PX≥t(X≥t+h)=P(X≥h)P_{X\ge t} \left(X\ge t+h\right)=P\left(X\ge h\right)

L'énoncé fournit :
PX≥650(X≥800)=PX≥650(X≥650+150)P_{X\ge 650} \left(X\ge 800\right)=P_{X\ge 650} \left(X\ge 650+150\right)
D'où : PX≥650(X≥800)=P(X≥150)P_{X\ge 650} \left(X\ge 800\right)=P\left(X\ge 150\right)
Ainsi :
PX≥650(X≥800)=e−0,01×150P_{X\ge 650} \left(X\ge 800\right)=e^{-0,01\times 150}
Question 12

Soit aa un nombre réel.
La variable aléatoire XX suit la loi uniforme sur [2;a]\left[2;a\right].
On sait que P(X≤12)=0,7P\left(X\le 12\right)=0,7.
La valeur de aa est :
  • 16,2816,28
  • 1212
  • 1717
  • 1147\frac{114}{7}

Correction
La proposition correcte est la proposition d.
La fonction de densité de probabilité de la loi uniforme sur [2;a]\left[2;a\right] est f(x)=1a−2f\left(x\right)=\frac{1}{a-2}
P(X≤12)=0,7P\left(X\le 12\right)=0,7
P(2≤X≤12)=0,7P\left(2\le X\le 12\right)=0,7
∫2121a−2dx=0,7\int _{2}^{12}\frac{1}{a-2} dx =0,7
[(1a−2)x]212=0,7\left[\left(\frac{1}{a-2} \right)x\right]_{2}^{12} =0,7
(1a−2)×12−(1a−2)×2=0,7\left(\frac{1}{a-2} \right)\times 12-\left(\frac{1}{a-2} \right)\times 2=0,7
12a−2−2a−2=0,7\frac{12}{a-2} -\frac{2}{a-2} =0,7
10a−2=0,7\frac{10}{a-2} =0,7
10=0,7×(a−2)10=0,7\times \left(a-2\right)
0,7×(a−2)=100,7\times \left(a-2\right)=10
0,7a−1,4=100,7a-1,4=10
0,7a=10+1,40,7a=10+1,4
0,7a=11,40,7a=11,4
a=11,40,7a=\frac{11,4}{0,7}
a=1147a=\frac{114}{7}
Question 13
Soit XX une variable aléatoire réelle . On admet que celle-ci suit une loi normale de moyenne μ=600\mu=600 et d’écart-type σ=74,6\sigma = 74,6.

La fonction densité associée à XX est représentée sur un seul de trois graphiques ci-dessous. Quel est ce graphique? Expliquer le choix.
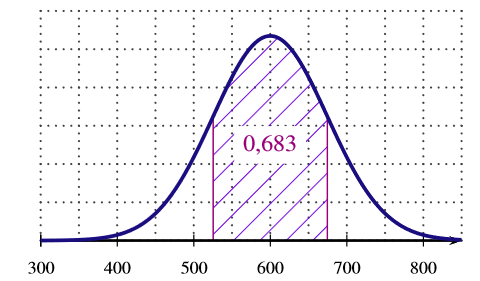
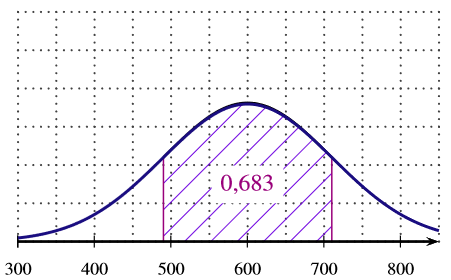
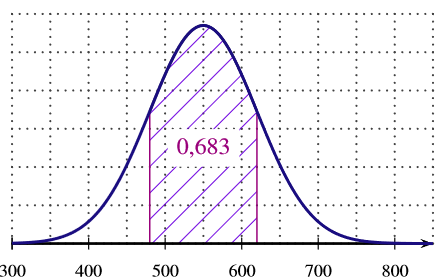
  • aucun des graphiques ne correspond à la fonction de densité XX

Correction
La proposition correcte est a.
Si XX suit une loi normale de paramètre μ\mu et σ\sigma alors :
  • P(μ−σ≤X≤μ+σ)=0,683P\left(\mu -\sigma \le X\le \mu +\sigma \right)=0,683
  • P(μ−2σ≤X≤μ+2σ)=0,954P\left(\mu -2\sigma \le X\le \mu +2\sigma \right)=0,954
  • P(μ−3σ≤X≤μ+3σ)=0,997P\left(\mu -3\sigma \le X\le \mu +3\sigma \right)=0,997
    • L'aire hachurée correspond à une aire de 0,6830,683. Ce qui signifie qu'il faut utiliser P(μ−σ≤X≤μ+σ)=0,683P\left(\mu -\sigma \le X\le \mu +\sigma \right)=0,683. Avec les données de l'exercice, il vient alors que :
    P(600−74,6≤X≤600+74,6)=0,683P\left(600-74,6\le X\le 600+74,6\right)=0,683 ainsi P(525,4≤X≤674,6)=0,683P\left(525,4\le X\le 674,6\right)=0,683
    Il n'y a que le graphique de la réponse aa qui donne des valeurs de XX comprise entre 525,4525,4 et 674,6674,6.