La géométrie dans l'espace et produit scalaire
Exercices types : ère partie - Exercice 1
20 min
30
Pour chacune des cinq propositions suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.
Question 1
L'espace est muni d'un repère orthonormé . On considère les points , , et
Proposition 1 : Les points , et définissent un plan.
Correction
En effet, on a :
et . On remarque que : . Les vecteurs et sont colinéaires. Donc les trois points , et sont alignés et ne définissent pas un plan.
Question 2
On admet que les points , et définissent un plan.
Proposition 2 : Une équation cartésienne du plan est : .
Correction
On vérifie facilement que les coordonnées de chacun des points , et vérifient l’équation .
En effet :
Question 3
Proposition 3 : Une représentation paramétrique de la droite est où
Correction
- Ici ne calculez pas l'équation de la droite car vous ne trouverez pas celle qui est donnée. En effet, il y a une infinité d'écriture paramétrique possible pour une droite.
Vérifiez simplement si les points et appartiennent à la droite qui vous a été donnée dans l'énoncé.
On remplace les coordonnées de dans l'équation paramétrique proposée :
Donc ce qui donne
Puis on résout les équations et on doit pour chaque ligne trouver la même valeur de pour que le point appartienne à la représentation paramétrique.
Ainsi .
Donc le point n'appartient à la représentation paramétrique donnée.
Donc où ne correspond pas à la représentation paramétrique de la droite .
Question 4
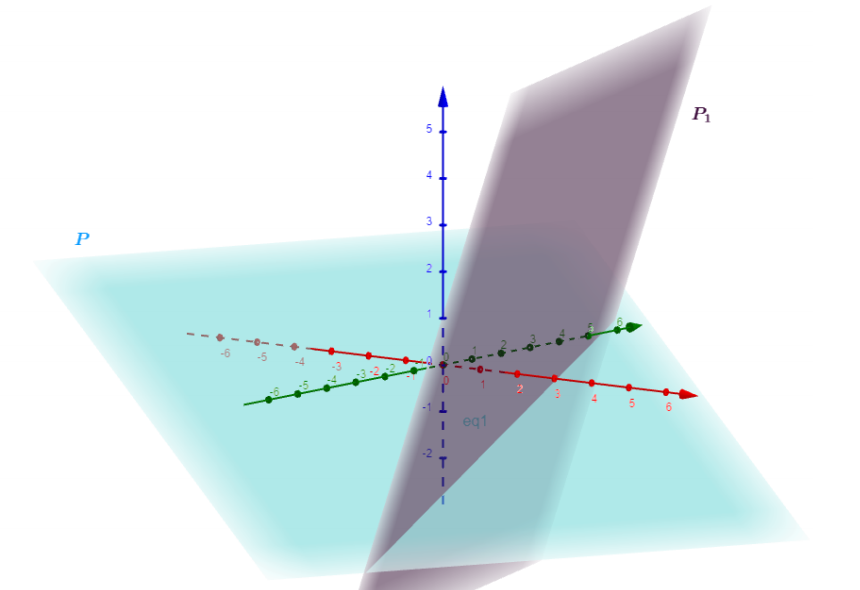
Soient le plan d'équation cartésienne : et le plan d'équation cartésienne :
Proposition 4 : Les plans et sont parallèles.
Correction
- Soient et des vecteurs normaux respectifs des plans et .
- si et sont colinéaires alors et sont parallèles.
- si et ne sont pas colinéaires alors et ne sont pas parallèles.
On vérifie facilement que les deux vecteurs normaux ne sont pas colinéaires (non proportionnels), alors les plans et ne sont pas parallèles.
Question 5
On se place dans l'espace muni d'un repère orthonormé .
On considère le plan d'équation et la droite dont une représentation paramétrique est où .
On considère le plan d'équation et la droite dont une représentation paramétrique est où .
Proposition 5 : la droite et le plan sont strictement parallèles.
Correction
Etape 1
Commencer par vérifier si le plan et la droite ne sont pas parallèles, par conséquent le plan et la droite sont sécants.
Etape 2
Il faut résoudre le système constitué de l'écriture paramétrique de la droite et du plan pour déterminer la valeur de
Ensuite, on substitue la valeur dans la droite pour obtenir les coordonnées du point d'intersection entre le plan et la droite.
Commencer par vérifier si le plan et la droite ne sont pas parallèles, par conséquent le plan et la droite sont sécants.
Etape 2
Il faut résoudre le système constitué de l'écriture paramétrique de la droite et du plan pour déterminer la valeur de
Ensuite, on substitue la valeur dans la droite pour obtenir les coordonnées du point d'intersection entre le plan et la droite.
Soient : un vecteur normal du plan et un vecteur directeur de
Donc et sont parallèles.
Maintenant est-ce que la droite et le plan sont confondus ?
Pour cela on résout le système :
où
On remplace la valeur de et dans le plan
Ainsi :
est une équation toujours vraie.
Cela signifie que le plan et la droite sont confondus.
La droite est incluse dans le plan .