La géométrie dans l'espace et produit scalaire
Exercice 6 - Exercice 1
1 min
0
On donne la propriété suivante : « par un point de l'espace il passe un plan et un seul orthogonal à une droite donnée »
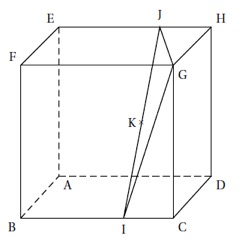
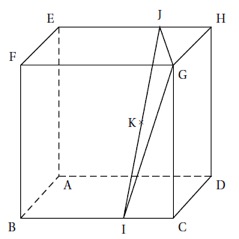
Sur la figure donnée ci-dessous, on a représenté le cube ABCDEFGH d'arête 1.
On a placé :
Les points et tels que et .
Le milieu de.
On appelle le projeté orthogonal de G sur le plan .
Sur la figure donnée ci-dessous, on a représenté le cube ABCDEFGH d'arête 1.
On a placé :
Les points et tels que et .
Le milieu de.
On appelle le projeté orthogonal de G sur le plan .

Question 1
Partie A
Démontrer que le triangle est isocèle en .
En déduire que les droites et sont orthogonales.
En déduire que les droites et sont orthogonales.
Correction
On a , dans le triangle rectangle en , on a .
Ainsi .
De même , dans le triangle rectangle en , on a donc .
, donc le triangle est isocèle en .
étant le milieu de , la droite médiane du triangle isocèle est aussi hauteur, donc perpendiculaire à .
Ainsi .
De même , dans le triangle rectangle en , on a donc .
, donc le triangle est isocèle en .
étant le milieu de , la droite médiane du triangle isocèle est aussi hauteur, donc perpendiculaire à .
Question 2
On admet que les droites et sont orthogonales.
Démontrer que la droite est orthogonale au plan .
Correction
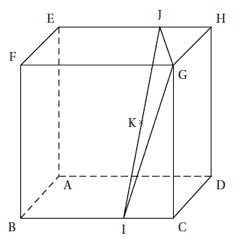
Question 3
Démontrer que la droite est orthogonale au plan .
Correction
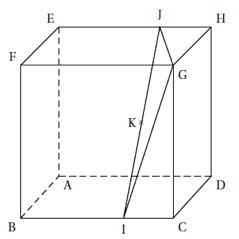
De même est orthogonale au plan , donc en particulier est orthogonale à .
Les points , et non alignés définissent un plan .
La droite orthogonale à deux droites sécantes de ce plan est orthogonale à ce plan .
Question 4
Montrer que les points , , et sont coplanaires.
Correction
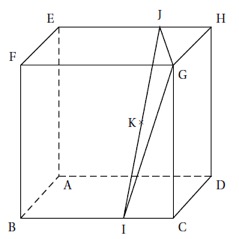
Mais ces deux plans contiennent le point .
Il n'existe qu'un plan contenant un point et orthogonal à une droite donnée, donc , , et sont coplanaires.
Question 5
En déduire que les points , , sont alignés.
Correction
Les points , , et sont coplanaires donc les points , et appartiennent au plan .
Conclusion
, et appartiennent aux plans et ; ces plans n'étant pas parallèles, leur intersection est une droite qui contient , et ; donc les points , et sont alignés.
Question 6
Partie B
L'espace est rapporté au repère orthonormal .
On appelle le point d'intersection de la droite et du plan .
On note les coordonnées du point .
L'espace est rapporté au repère orthonormal .
On appelle le point d'intersection de la droite et du plan .
On note les coordonnées du point .
Donner les coordonnées des points , , et .
Correction
Si l'on veut déterminer les coordonnées par exemple d'un point il faut l'exprimer le point avec l'origine du repère en fonction des vecteurs du repère donné. Dans notre exemple, si alors les coordonnées de sont .
On a :
; donc
; donc
; donc
; donc
Question 7
Montrer que la droite est orthogonale aux droites et .
Correction
a pour projeté orthogonal sur le plan le point , donc est orthogonale à .
appartient à la droite , donc est orthogonale à donc à toute droite de ce plan.
Conclusion : est orthogonale à et à .
appartient à la droite , donc est orthogonale à donc à toute droite de ce plan.
Conclusion : est orthogonale à et à .
Question 8
Exprimer les produits scalaires et en fonction de et .
Correction
On a ; et
D'une part :
D'autre part :
D'une part :
D'autre part :
Question 9
Déterminer les coordonnées du point .
Correction
D'après la question , les deux produits scalaires ci-dessus sont nuls car la droite est orthogonale aux droites et .
Ainsi,
D'une part,
D'autre part,
Les cordonnées de sont donc .
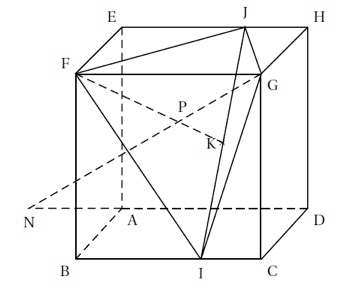
On a le résumé de tout ce que l'on a fait sur la figure ci-dessous :
Ainsi,
D'une part,
D'autre part,
Les cordonnées de sont donc .
On a le résumé de tout ce que l'on a fait sur la figure ci-dessous :
