La fonction logarithme
Variations - Exercice 1
35 min
50
Etudier les variations des fonctions suivantes
Question 1
sur
Correction
est dérivable sur .
. Nous allons tout mettre au même dénominateur .
Cela signifie que l'on mettra le signe pour le signe de dès que . Or nous travaillons sur l'intervalle . Cela signifie donc que est positive sur .

. Nous allons tout mettre au même dénominateur .
Cela signifie que l'on mettra le signe pour le signe de dès que . Or nous travaillons sur l'intervalle . Cela signifie donc que est positive sur .

Question 2
sur
Correction
est dérivable sur .
. Nous allons tout mettre au même dénominateur .
Cela signifie que l'on mettra le signe pour le signe de dès que
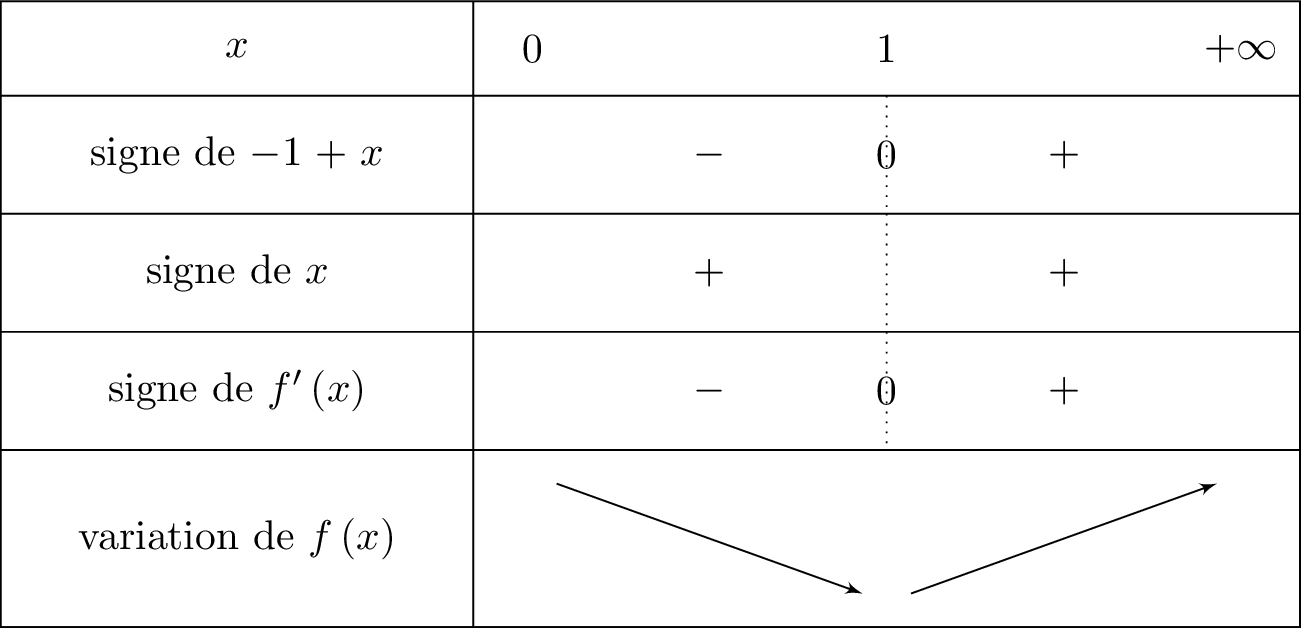
. Nous allons tout mettre au même dénominateur .
Cela signifie que l'on mettra le signe pour le signe de dès que

Question 3
sur
Correction
(ensuite toujours mettre au même dénominateur)
Ainsi :
Comme on travaille sur l'intervalle alors le dénominateur est strictement positif.
Il en résulte que le signe de dépend du numérateur .
est une équation du second degré, pour étudier son signe on va utiliser le discriminant .
On donnera directement les résultats : ; et .
Comme , la parabole est tournée vers le bas c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
Pour nous aider on va donner pour le moment le signe de sur (vous ne devrez en aucun cas le faire sur votre copie c'est juste pour nous aider)
 On n'oublie pas que nous devons étudier les variations de sur .
On n'oublie pas que nous devons étudier les variations de sur .
On en déduit maintenant le tableau de variation de sur :
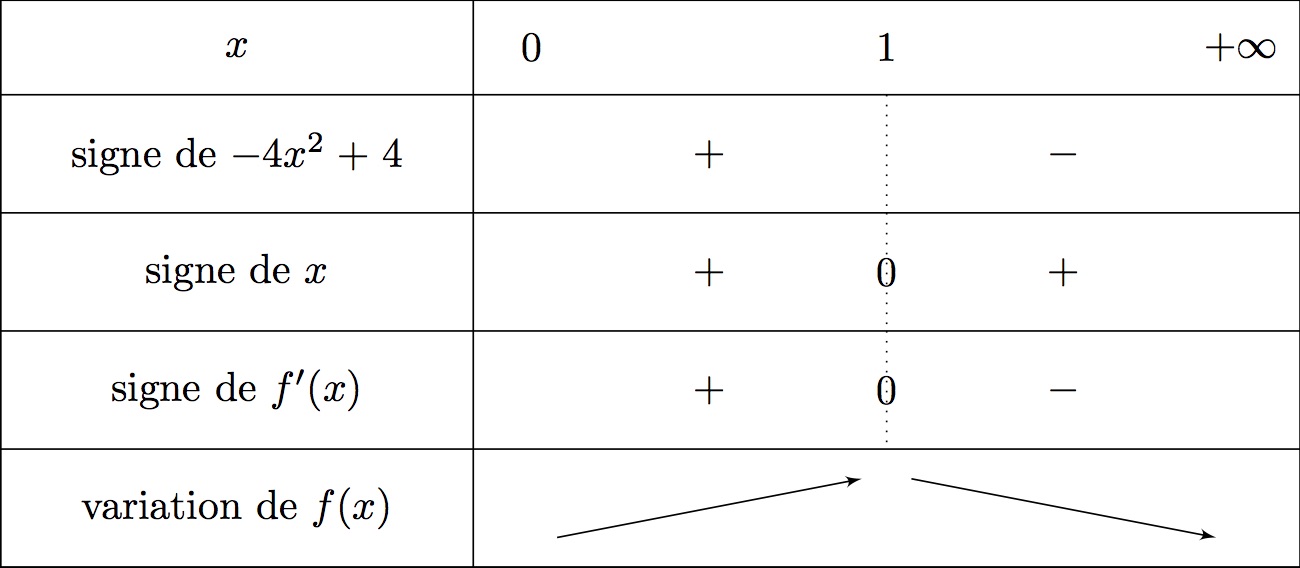
Ainsi :
Comme on travaille sur l'intervalle alors le dénominateur est strictement positif.
Il en résulte que le signe de dépend du numérateur .
est une équation du second degré, pour étudier son signe on va utiliser le discriminant .
On donnera directement les résultats : ; et .
Comme , la parabole est tournée vers le bas c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
Pour nous aider on va donner pour le moment le signe de sur (vous ne devrez en aucun cas le faire sur votre copie c'est juste pour nous aider)

On en déduit maintenant le tableau de variation de sur :

Question 4
sur
Correction
est dérivable sur .
On reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Ainsi :
Cela signifie que l'on mettra le signe pour le signe de dès que
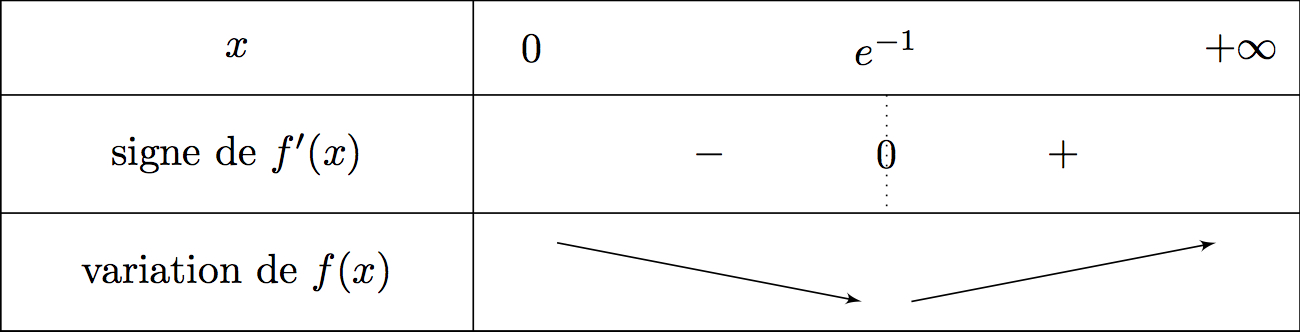
On reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Ainsi :
Cela signifie que l'on mettra le signe pour le signe de dès que

Question 5
sur
Correction
est dérivable sur .
On reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Ainsi :
Comme alors et donc le signe de dépend de
Cela signifie que l'on mettra le signe pour le signe de dès que
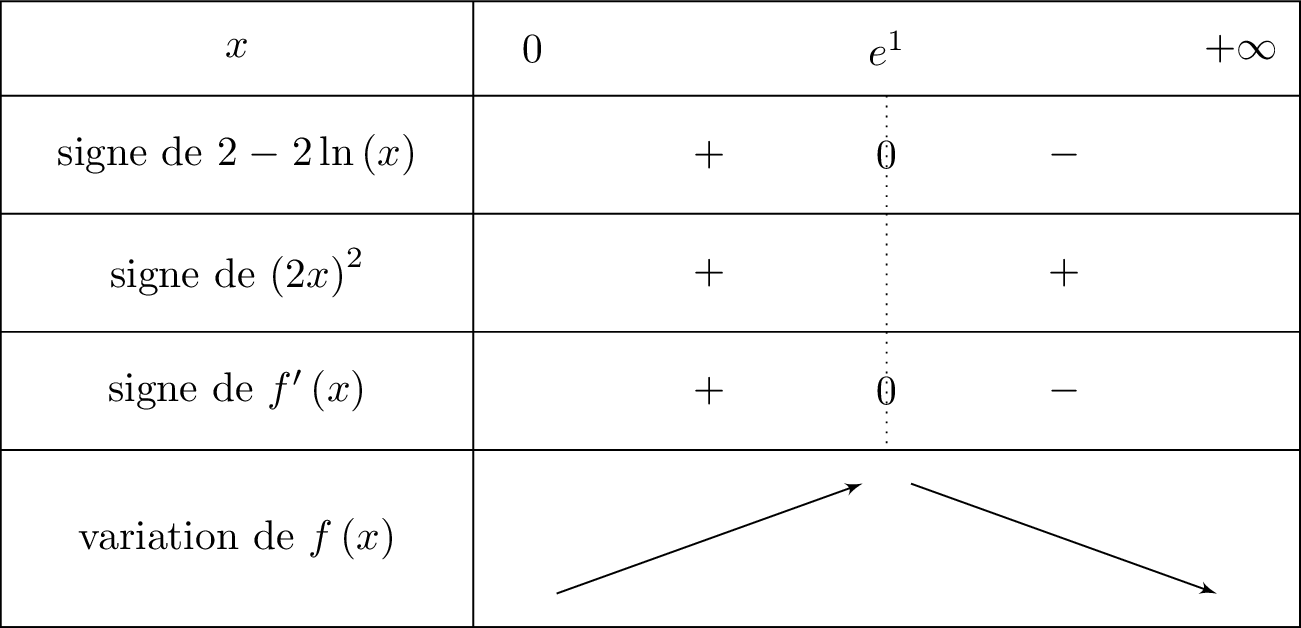
On reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Ainsi :
Comme alors et donc le signe de dépend de
Cela signifie que l'on mettra le signe pour le signe de dès que

Question 6
sur
Correction
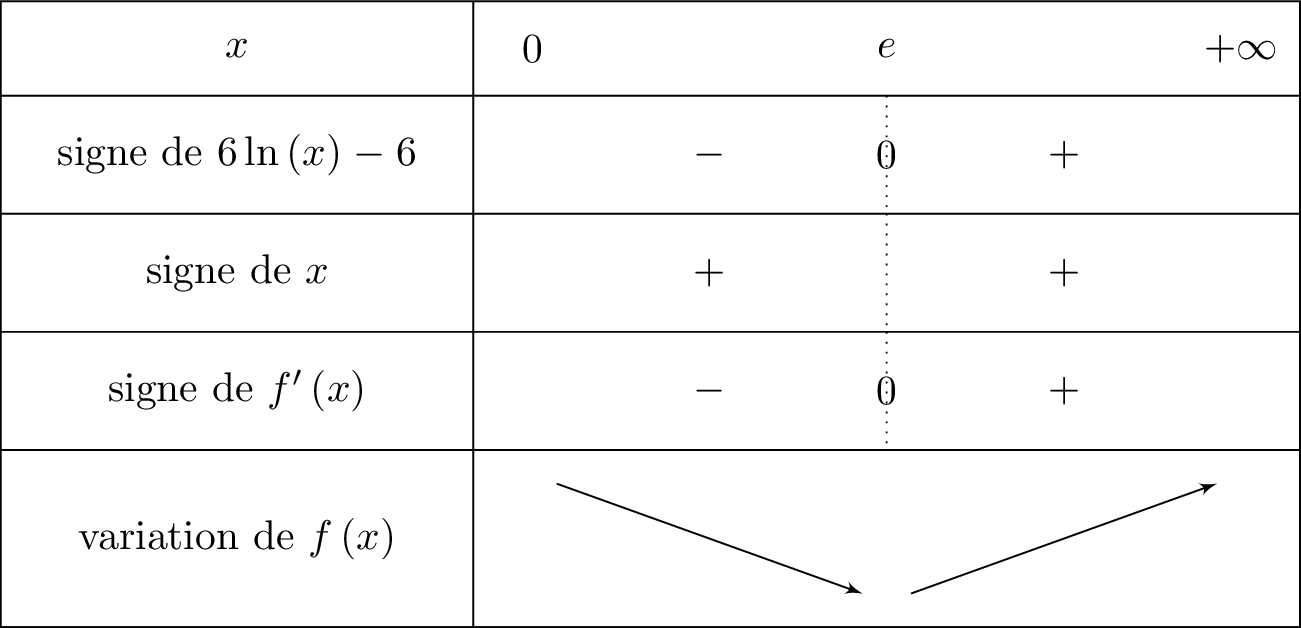
Notons , il en résulte donc que : .
Nous allons pouvoir maintenant calculer la dérivée de . Ainsi :
est dérivable sur .
Comme alors et donc le signe de dépend de .
Cela signifie que l'on mettra le signe pour le signe de dès que
Question 7
sur
Correction
est dérivable sur .
On reconnaît la forme avec ; et .
Ainsi ; et .
Il vient alors que :
Le signe de dépend donc de .
Cela signifie que l'on mettra le signe pour le signe de dès que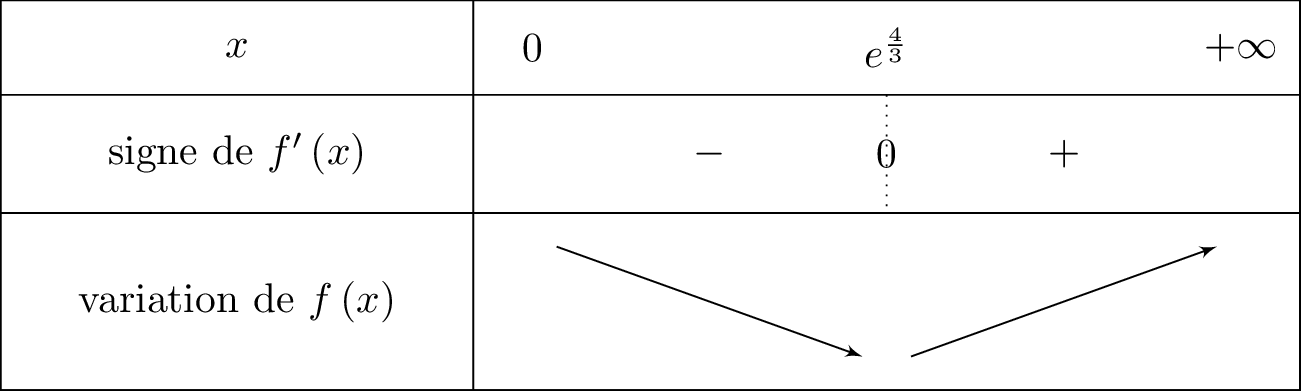
On reconnaît la forme avec ; et .
Ainsi ; et .
Il vient alors que :
Le signe de dépend donc de .
Cela signifie que l'on mettra le signe pour le signe de dès que

Question 8
sur
Correction
est dérivable sur .
On reconnaît ici où et . Ainsi .
Il en résulte que :
Finalement :
Pour tout réel , on vérifie aisément que et . Il en résulte donc que le signe de dépend de .
Cela signifie que l'on mettra le signe pour le signe de dès que .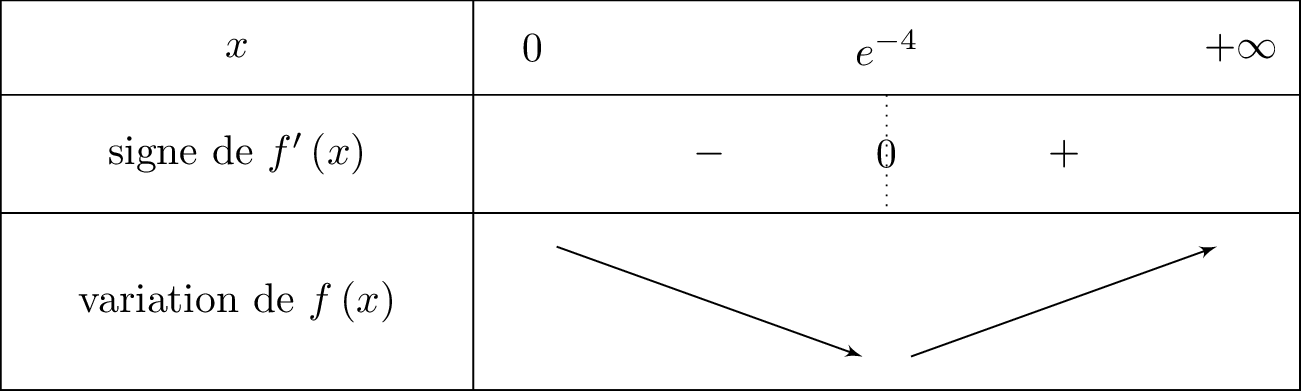
Il en résulte que :
Finalement :
Pour tout réel , on vérifie aisément que et . Il en résulte donc que le signe de dépend de .
Cela signifie que l'on mettra le signe pour le signe de dès que .
