La fonction exponentielle
A la mode au bac : des exponentielles et des sciences physiques - Exercice 1
1 h 5 min
95
Les parties et peuvent être traitées de façon indépendante.
Dans une usine, un four cuit des céramiques à la température de °C. À la fin de la cuisson, il est éteint et il refroidit. On s’intéresse à la phase de refroidissement du four, qui débute dès l’instant où il est éteint. La température du four est exprimée en degré Celsius (°C). La porte du four peut être ouverte sans risque pour les céramiques dès que sa température est inférieure à ° C. Sinon les céramiques peuvent se fissurer, voire se casser.
Dans une usine, un four cuit des céramiques à la température de °C. À la fin de la cuisson, il est éteint et il refroidit. On s’intéresse à la phase de refroidissement du four, qui débute dès l’instant où il est éteint. La température du four est exprimée en degré Celsius (°C). La porte du four peut être ouverte sans risque pour les céramiques dès que sa température est inférieure à ° C. Sinon les céramiques peuvent se fissurer, voire se casser.
Question 1
Partie . Pour un nombre entier naturel , on note la température en degré Celsius du four au bout de heures écoulées à partir de l’instant où il a été éteint. On a donc . La température est calculée par l’algorithme suivant :
Pour allant de à
Fin Pour
Pour allant de à
Fin Pour
Déterminer la température du four, arrondie à l’unité, au bout de heures de refroidissement.
Correction
Il nous faut calculer les ; et pour obtenir .
De plus, pour les calculs intermédiaires, nous allons donner les valeurs exactes afin de faire l'arrondi que pour la valeur de .
Il vient alors que :
d'où : ainsi :
d'où : ainsi :
d'où :
d'où :
La température du four, arrondie à l’unité, au bout de heures de refroidissement est alors de °C.
On peut aussi en conclure que d'après l'algorithme que :
De plus, pour les calculs intermédiaires, nous allons donner les valeurs exactes afin de faire l'arrondi que pour la valeur de .
Il vient alors que :
d'où : ainsi :
d'où : ainsi :
d'où :
d'où :
La température du four, arrondie à l’unité, au bout de heures de refroidissement est alors de °C.
On peut aussi en conclure que d'après l'algorithme que :
Question 2
Démontrer que, pour tout nombre entier naturel , on a :
Correction
Nous allons procéder par récurrence.
Pour tout entier naturel , posons la propriété
Etape d'initialisation
On sait que et que .
La propriété est vraie.
Etape d'hérédité
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire
Par hypothèse de récurrence :
, on multiplie par de part et d'autre de l'égalité
. On va maintenant additionner par de part et d'autre de l'égalité (notre objectif est de faire apparaître dans le membre de gauche )
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , on a bien :
Pour tout entier naturel , posons la propriété
Etape d'initialisation
On sait que et que .
La propriété est vraie.
Etape d'hérédité
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire
Par hypothèse de récurrence :
, on multiplie par de part et d'autre de l'égalité
. On va maintenant additionner par de part et d'autre de l'égalité (notre objectif est de faire apparaître dans le membre de gauche )
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , on a bien :
Question 3
Au bout de combien d’heures le four peut-il être ouvert sans risque pour les céramiques?
Correction
La porte du four peut être ouverte sans risque pour les céramiques dès que sa température est inférieure à ° C. Il nous faut donc résoudre
équivaut successivement à :
Il nous faut donc que .
Cela signifie que l'on pourra ouvrir le four au bout de heures.
équivaut successivement à :
Il nous faut donc que .
Cela signifie que l'on pourra ouvrir le four au bout de heures.
Question 4
Partie
Dans cette partie, on note le temps (en heure) écoulé depuis l’instant où le four a été éteint. La température du four (en degré Celsius) à l’instant est donnée par la fonction définie, pour tout nombre réel positif, par : où et sont deux nombres réels.
On admet que vérifie la relation suivante :
Dans cette partie, on note le temps (en heure) écoulé depuis l’instant où le four a été éteint. La température du four (en degré Celsius) à l’instant est donnée par la fonction définie, pour tout nombre réel positif, par : où et sont deux nombres réels.
On admet que vérifie la relation suivante :
Déterminer les valeurs de et sachant qu’initialement, la température du four est de °C, c’est-à-dire que .
Correction
D'une part :
Il vient alors que :
équivaut successivement à :
D'autre part :
. Il nous faut commencer par calculer la dérivée de
Ainsi :
D'où :
Nous allons maintenant résoudre cette équation : .
équivaut successivement à :
Il vient alors que :
Or , nous savons aussi, que : ce qui nous donne
Finalement :
Il vient alors que :
équivaut successivement à :
D'autre part :
. Il nous faut commencer par calculer la dérivée de
Ainsi :
D'où :
Nous allons maintenant résoudre cette équation : .
équivaut successivement à :
Il vient alors que :
Or , nous savons aussi, que : ce qui nous donne
.
Finalement :
Question 5
Pour la suite, on admet que, pour tout nombre réel positif : .
Déterminer la limite de lorsque tend vers .
Correction
Ici, il s'agit d'une limite par composition.
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Finalement :
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Finalement :
Question 6
Étudier les variations de sur . En déduire son tableau de variations complet.
Correction
est dérivable sur .
Pour tout réel positif, on vérifie aisément que et .
Il en résulte donc que et de ce fait la fonction est strictement décroissante.
Nous dressons ci-dessous le tableau de variation complet de .
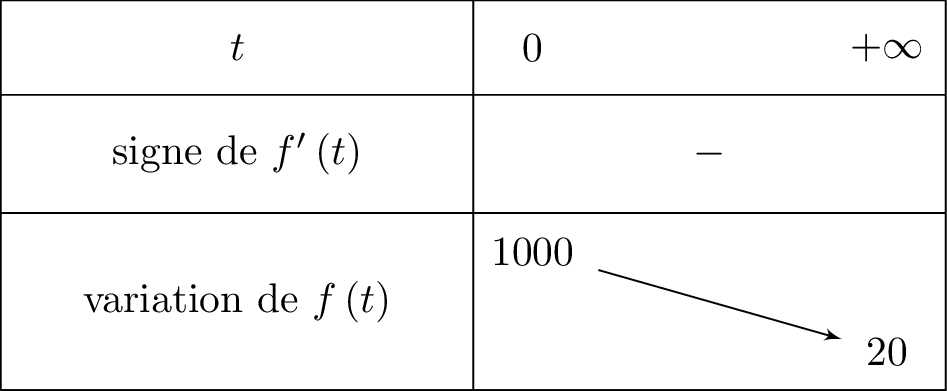
Pour tout réel positif, on vérifie aisément que et .
Il en résulte donc que et de ce fait la fonction est strictement décroissante.
Nous dressons ci-dessous le tableau de variation complet de .

Question 7
Avec ce modèle, après combien de minutes le four peut-il être ouvert sans risque pour les céramiques?
Correction
La porte du four peut être ouverte sans risque pour les céramiques dès que sa température est inférieure à ° C
Ainsi :
On trouve alors heures ce qui nous donne minutes.
Ainsi :
On trouve alors heures ce qui nous donne minutes.
Question 8
La température moyenne (en degré Celsius) du four entre deux instants et est donnée par :
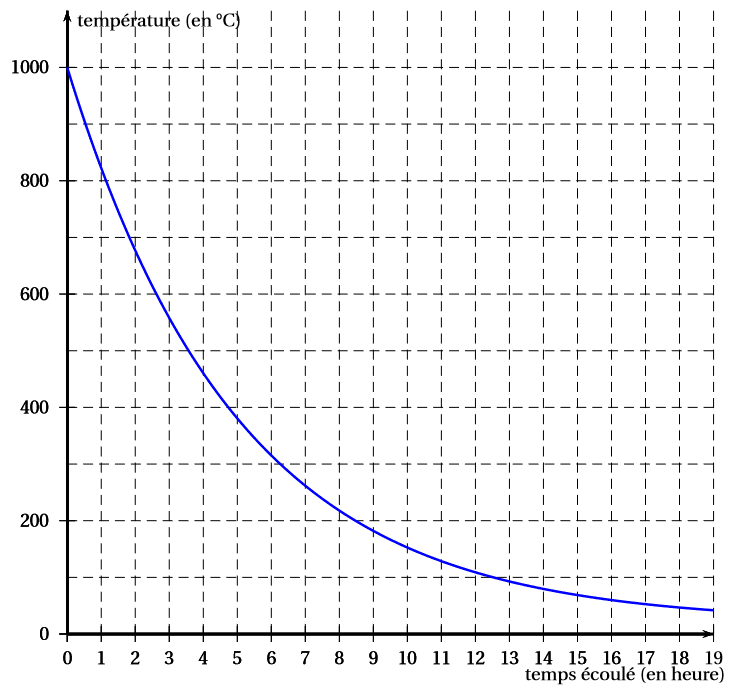
À l’aide de la représentation graphique de ci-dessous, donner une estimation de la température moyenne du four sur les premières heures de refroidissement. Expliquer votre démarche.

Correction
Il nous faut estimer l'aire sous la courbe entre et puis la diviser par .
Le quadrillage donne une aire d'environ carreaux , d'aire chacun, donc une valeur moyenne d'environ . Vu les erreurs d'arrondi, on peut annoncer une température moyenne d'environ °C.
Le quadrillage donne une aire d'environ carreaux , d'aire chacun, donc une valeur moyenne d'environ . Vu les erreurs d'arrondi, on peut annoncer une température moyenne d'environ °C.
Question 9
Calculer la valeur exacte de cette température moyenne et en donner la valeur arrondie au degré Celsius.
Correction
Ainsi :
La valeur arrondie au degré Celsius est alors °C.
Question 10
Dans cette question, on s’intéresse à l’abaissement de température (en degré Celsius) du four au cours d’une heure, soit entre deux instants et . Cet abaissement est donné par la fonction définie, pour tout nombre réel positif, par : .
Vérifier que, pour tout nombre réel positif , on a :
Correction
Nous savons que alors .
équivaut successivement à :
équivaut successivement à :
Question 11
Déterminer la limite de lorsque tend vers . Quelle interprétation peut-on en donner ?
Correction
D'après la question , on sait que :
Donc l'écart entre les heures tend à s'estomper : la température décroit de plus en plus lentement.
Donc l'écart entre les heures tend à s'estomper : la température décroit de plus en plus lentement.