Estimation et intervalles
Exercice 3 - Exercice 1
1 min
0
Une entreprise produit à la chaîne des jouets pesant en moyenne g.
Suite à une étude statistique, on considère que la masse d'un jouet est une variable aléatoire qui suit la loi normale d'espérance et d'écart-type .
Dans tout l'exercice les résultats seront arrondis à .
Suite à une étude statistique, on considère que la masse d'un jouet est une variable aléatoire qui suit la loi normale d'espérance et d'écart-type .
Dans tout l'exercice les résultats seront arrondis à .
Question 1
Déterminer .
Interpréter ce résultat.
Interpréter ce résultat.
Correction
Pour le calcul de
Avec une Texas, on tape pour NormalFrep(valeur min,valeur max ,espérance , écart type ) c'est-à-dire ici NormalFrep( , , , ) puis taper sur enter et vous obtiendrez
Avec une Casio Graph 35+, on tape pour
puis taper sur EXE et vous obtiendrez
Cela signifie qu'avec ce modèle il devrait y avoir des jouets dont la masse en grammes est comprise entre et .
Avec une Texas, on tape pour NormalFrep(valeur min,valeur max ,espérance , écart type ) c'est-à-dire ici NormalFrep( , , , ) puis taper sur enter et vous obtiendrez
Avec une Casio Graph 35+, on tape pour
Normal C.D
Lower : Valeur Minimale
Upper : Valeur Maximale
: Ecart type
: Espérance
Lower : Valeur Minimale
Upper : Valeur Maximale
: Ecart type
: Espérance
puis taper sur EXE et vous obtiendrez
Cela signifie qu'avec ce modèle il devrait y avoir des jouets dont la masse en grammes est comprise entre et .
Question 2
Justifier, en utilisant des propriétés du cours, que .
Correction
D'après les propriétés de la loi normale, on sait que .
On peut donc, pour des raisons de symétrie de la courbe en cloche, déduire que (en bleu) et que (en vert)
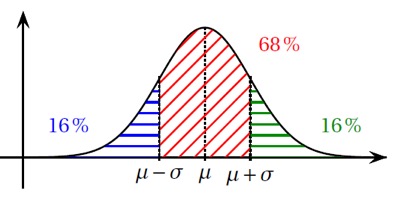 Or et donc , et donc
Or et donc , et donc
On peut donc, pour des raisons de symétrie de la courbe en cloche, déduire que (en bleu) et que (en vert)

Question 3
Un jouet est commercialisable s'il pèse au maximum g.
Quelle est la probabilité que le jouet soit commercialisable ?
Quelle est la probabilité que le jouet soit commercialisable ?
Correction
Un jouet est commercialisable s'il pèse au maximum g.
Pour le calcul de
Avec une Texas, on tape pour NormalFrep(valeur min,valeur max ,espérance , écart type ) c'est-à-dire ici NormalFrep( , , , ) puis taper sur enter et vous obtiendrez
Avec une Casio Graph 35+, on tape pour
puis taper sur EXE et vous obtiendrez
La probabilité qu'un jouet soit commercialisable est de .
On cherche à contrôler la qualité des jouets.
Pour cela on choisit de façon aléatoire un échantillon de jouets.
Pour le calcul de
Avec une Texas, on tape pour NormalFrep(valeur min,valeur max ,espérance , écart type ) c'est-à-dire ici NormalFrep( , , , ) puis taper sur enter et vous obtiendrez
Avec une Casio Graph 35+, on tape pour
Normal C.D
Lower : Valeur Minimale
Upper : Valeur Maximale
: Ecart type
: Espérance
Lower : Valeur Minimale
Upper : Valeur Maximale
: Ecart type
: Espérance
puis taper sur EXE et vous obtiendrez
La probabilité qu'un jouet soit commercialisable est de .
On cherche à contrôler la qualité des jouets.
Pour cela on choisit de façon aléatoire un échantillon de jouets.
Question 4
Vérifier que les conditions de détermination de l'intervalle de fluctuation asymptotique au seuil de de la fréquence de jouets commercialisables sont vérifiées.
Correction
Les conditions de détermination de l'intervalle de fluctuation asymptotique au seuil de 95% de la fréquence de jouets commercialisables sont : , et .
et et .
Les conditions sont donc vérifiées.
et et .
Les conditions sont donc vérifiées.
Question 5
Déterminer cet intervalle.
Correction
L'intervalle de fluctuation asymptotique au seuil de de la fréquence de jouets commercialisables est :
Ici est une valeur approchée par défaut de
Ici est une valeur approchée par excès de
Ici est une valeur approchée par défaut de
Ici est une valeur approchée par excès de
Question 6
On constate que jouets de l'échantillon sont commercialisables.
Ce résultat remet-il en question la modélisation effectuée par l'entreprise ?
Correction
On constate que jouets de l'échantillon sont commercialisables, ce qui fait une fréquence observée de .
Or donc ce résultat remet en cause la modélisation effectuée par l'entreprise.
Or donc ce résultat remet en cause la modélisation effectuée par l'entreprise.