Les lois continues
Exercice 1 - Exercice 1
1 min
0
Cet exercice est un questionnaire à choix multiples.
Chaque question ci-après comporte quatre propositions de réponse.
Pour chacune de ces questions, une seule des réponses proposées est exacte.
On demande bien sûr de justifier.
Chaque question ci-après comporte quatre propositions de réponse.
Pour chacune de ces questions, une seule des réponses proposées est exacte.
On demande bien sûr de justifier.
Question 1
Partie A
Un fumeur est dit fumeur régulier s'il fume au moins une cigarette par jour.
En , en France, la proportion notée de fumeurs réguliers, âgés de à ans, était de .
On a .
La probabilité que, sur un groupe de jeunes âgés de à ans choisis au hasard et de manière indépendante, aucun ne soit fumeur régulier est, à près :
En , en France, la proportion notée de fumeurs réguliers, âgés de à ans, était de .
On a .
La probabilité que, sur un groupe de jeunes âgés de à ans choisis au hasard et de manière indépendante, aucun ne soit fumeur régulier est, à près :
Correction
La proposition correcte est c.
Chaque choix de jeune peut être considéré comme une épreuve de Bernoulli.
Le succès est l'évènement « le jeune est fumeur régulier ».
La probabilité de succès est .
On répète épreuves de Bernoulli identiques et indépendantes.
Si on note la variable aléatoire correspondant au nombre de succès, suit la loi binomiale de paramètres et
. Utilisez votre calculatrice :)
Chaque choix de jeune peut être considéré comme une épreuve de Bernoulli.
Le succès est l'évènement « le jeune est fumeur régulier ».
La probabilité de succès est .
On répète épreuves de Bernoulli identiques et indépendantes.
Si on note la variable aléatoire correspondant au nombre de succès, suit la loi binomiale de paramètres et
Question 2
Un intervalle de fluctuation asymptotique au seuil de de la fréquence de fumeurs réguliers dans un échantillon de jeunes âgés de à ans est :
(les bornes de chaque intervalle sont données à près)
(les bornes de chaque intervalle sont données à près)
Correction
La proposition correcte est a.
La taille de l'échantillon est supérieur à .
On a également :
et
Pour la borne inférieure, on donne une valeur approchée par défaut.
Pour la borne supérieure, on donne une valeur approchée par excès.
La taille de l'échantillon est supérieur à .
On a également :
et
Pour la borne inférieure, on donne une valeur approchée par défaut.
Pour la borne supérieure, on donne une valeur approchée par excès.
Question 3
La taille de l'échantillon choisi afin que l'amplitude de l'intervalle de fluctuation au seuil de soit inférieure à , vaut :
Correction
La proposition correcte est d.
équivaut successivement à
Ensuite on inverse les deux quotients, le sens de l'inégalité changera.
Ainsi :
équivaut successivement à
Ensuite on inverse les deux quotients, le sens de l'inégalité changera.
Ainsi :
Question 4
Dans un échantillon de jeunes fumeurs réguliers, âgés de à ans, sont des filles.
(les bornes de chaque intervalle sont données à près)
(les bornes de chaque intervalle sont données à près)
Correction
La proposition correcte est b.
On a bien ; et .
L'intervalle de confiance au niveau de confiance est donné par la formule suivante.
On arrondit la borne inférieure par défaut.
On arrondit la borne supérieure par excès.
On a bien ; et .
L'intervalle de confiance au niveau de confiance est donné par la formule suivante.
On arrondit la borne inférieure par défaut.
On arrondit la borne supérieure par excès.
Question 5
Partie B
Cette partie est indépendante de la partie A.
Cette partie est indépendante de la partie A.
Pour la fête du village de Boisjoli, le maire a invité les enfants des villages voisins.
Les services de la mairie ayant géré les inscriptions dénombrent enfants à cette fête ; ils indiquent aussi que des enfants présents sont des enfants qui habitent le village de Boisjoli.
Le nombre d'enfants issus des villages voisins est :
Les services de la mairie ayant géré les inscriptions dénombrent enfants à cette fête ; ils indiquent aussi que des enfants présents sont des enfants qui habitent le village de Boisjoli.
Le nombre d'enfants issus des villages voisins est :
Correction
La proposition correcte est b.
Il y a d’enfants de Boisjoli, donc d’enfants des villages voisins :
D'où :
Il y a d’enfants de Boisjoli, donc d’enfants des villages voisins :
D'où :
Question 6
Lors de cette fête, huit enfants sont choisis au hasard afin de former une équipe qui participera à un défi sportif.
On admet que le nombre d'enfants est suffisamment grand pour que cette situation puisse être assimilée à un tirage au hasard avec remise.
On admet que le nombre d'enfants est suffisamment grand pour que cette situation puisse être assimilée à un tirage au hasard avec remise.
On appelle la variable aléatoire prenant pour valeurs le nombre d'enfants de l'équipe habitant le village de Boisjoli.
La variable aléatoire suit la loi binomiale de paramètres :
- et
- et
- et
- et
La variable aléatoire suit la loi binomiale de paramètres :
- et
- et
- et
- et
Correction
La proposition correcte est c.
La probabilité qu’un enfant soit de Boisjoli est puisqu’il y a d’enfants de ce village.
On choisit enfants donc
La probabilité qu’un enfant soit de Boisjoli est puisqu’il y a d’enfants de ce village.
On choisit enfants donc
Question 7
La probabilité que dans l'équipe il y ait au moins un enfant habitant le village de Boisjoli est :
Correction
La proposition correcte est c.
On cherche .
Or :
Avec la calculatrice on obtient :
On cherche .
Or :
Avec la calculatrice on obtient :
Question 8
L'espérance mathématique de est :
Correction
La proposition correcte est c.
est une variable aléatoire qui suit une loi binomiale , alors l’espérance mathématique , la variance et l’écart type sont égales à :
Donc : Question 9
Partie C
Cette partie est indépendante de la partie et de la partie .
Cette partie est indépendante de la partie et de la partie .
Dans un parc d'attraction, le temps d'attente pour profiter de l'attraction phare, exprimé en minutes, sur la loi uniforme sur l'intervalle
Quelle est la probabilité que le temps d'attente soit compris entre à minutes ?
Quelle est la probabilité que le temps d'attente soit compris entre à minutes ?
Correction
La proposition correcte est a.
Soit une variable aléatoire suivant la loi uniforme sur l'intervalle alors :
équivaut successivement à :Question 10
Préciser le temps d'attente moyen à la caisse :
Correction
La proposition correcte est b.
Il en résulte que :
Si suit la loi uniforme sur un intervalle alors son espérance mathématique vaut
Il en résulte que :
Question 11
Cette question est indépendante.
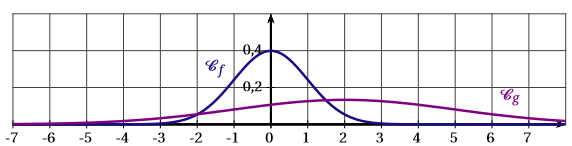
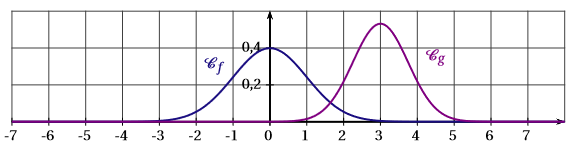
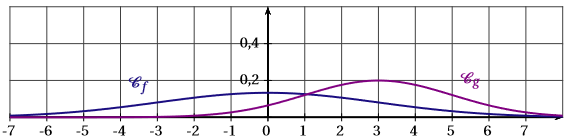
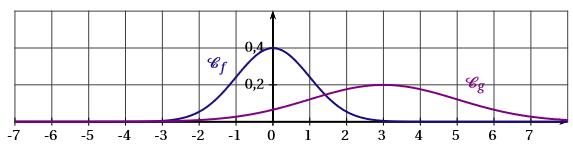
La fonction est la fonction densité de probabilité associée à la loi normale centrée réduite .
La fonction est la fonction de densité de probabilité associée à la loi normale de moyenne et d’écart-type .
La fonction est la fonction densité de probabilité associée à la loi normale centrée réduite .
La fonction est la fonction de densité de probabilité associée à la loi normale de moyenne et d’écart-type .
La représentation graphique de ces deux fonctions est :
Correction
- La fonction est la fonction de Gauss définie par . Ainsi : ce qui exclu automatiquement la courbe c.
- La courbe représentative de doit être symétrique par rapport à la droite d’équation ; cela exclut la courbe a.
- On sait également que : . Cela exclut la figure b, car l’aire correspondante entre et est visiblement supérieure à quatre carreaux, donc supérieure à .
Question 12
Cette question est indépendante.
Soit une variable aléatoire réelle . On admet que celle-ci suit une loi normale de moyenne et d’écart-type .
Soit une variable aléatoire réelle . On admet que celle-ci suit une loi normale de moyenne et d’écart-type .
La fonction densité associée à est représentée sur un seul de trois graphiques ci-dessous. Quel est ce graphique? Expliquer le choix.
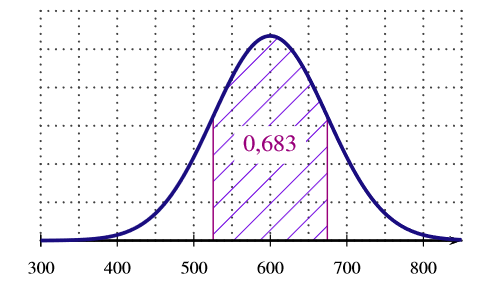
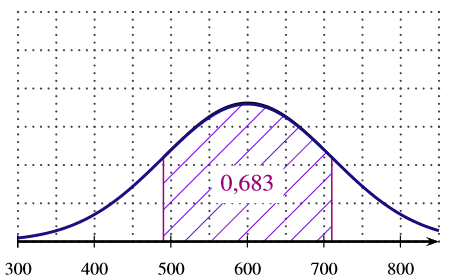
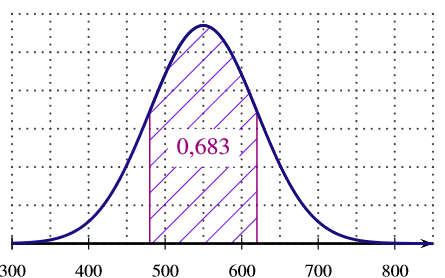
- aucun des graphiques ne correspond à la fonction de densité



- aucun des graphiques ne correspond à la fonction de densité
Correction
La proposition correcte est a.
ainsi
Il n'y a que le graphique de la réponse qui donne des valeurs de comprise entre et .
Si suit une loi normale de paramètre et alors :
L'aire hachurée correspond à une aire de . Ce qui signifie qu'il faut utiliser . Avec les données de l'exercice, il vient alors que :ainsi
Il n'y a que le graphique de la réponse qui donne des valeurs de comprise entre et .