La fonction logarithme
Exercice 9 - Exercice 1
1 min
0
Question 1
Soit la fonction définie sur par : . On note la courbe représentative de la fonction .
Calculer .
Correction
. Nous allons maintenant tout mettre au même dénominateur.
Question 2
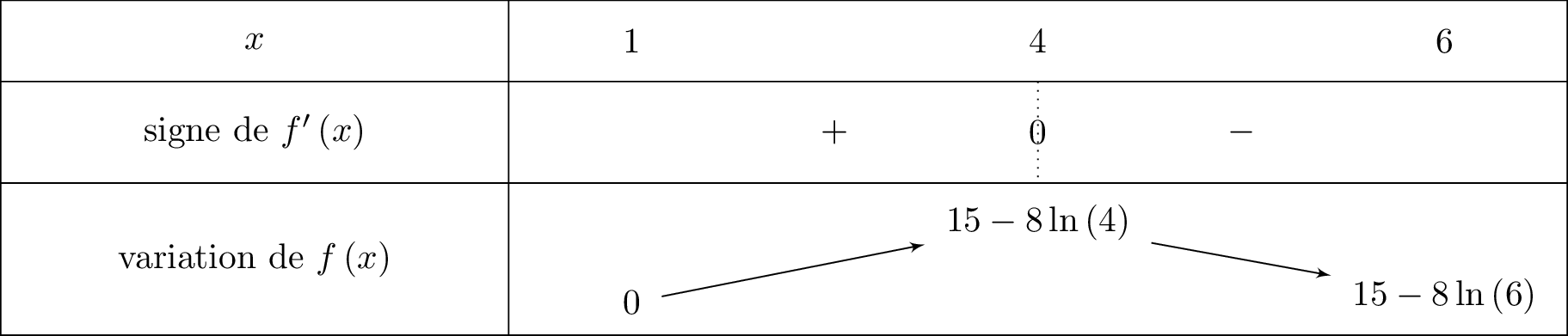
Etudier le signe de sur l'intervalle et dresser le tableau de variation de .
Correction
Sur l'intervalle , donc est du signe de .
On cherche le signe de .
On va utiliser le discriminant :
.
Il existe donc deux solutions que l'on note
Les racines du polynôme sont :
Comme , la parabole est tournée vers le haut c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
De plus :
On cherche le signe de .
On va utiliser le discriminant :
.
Il existe donc deux solutions que l'on note
Les racines du polynôme sont :
Comme , la parabole est tournée vers le haut c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
De plus :
- d'où :
- d'où :
- d'où :

Question 3
Soit une fonction définie sur
Prouver que est une primitive de la fonction
Correction
Dans le cas où une primitive est donnée, il vous suffit de dériver la primitive et d'obtenir comme résultat .
Autrement dit, dans notre cas, il faut montrer que : Soit .
Ici on reconnaît la forme : avec ; et .
Ainsi : ; et .
Il vient alors que :
équivaut successivement à :
D'où :
Nous venons de montrer que est une primitive de la fonction
Question 4
En déduire une primitive de la fonction sur l’intervalle .
Correction
Nous rappelons que : et nous savons également que est une primitive de la fonction .
Il en résulte donc que :
Il en résulte donc que :
Question 5
Calculer la valeur moyenne de la fonction sur l'intervalle . Donner la valeur exacte puis une valeur décimale arrondie au dixième.
Correction
une fonction continue sur un intervalle .
La valeur moyenne de la fonction sur est le réel défini par
On a :La valeur moyenne de la fonction sur est le réel défini par
. Il s'agit de la valeur exacte.
au dixième près.