Continuité, dérivation, lectures graphiques et convexité
Exercice 3 - Exercice 1
1 min
0
Cet exercice est un questionnaire à choix multiples.
Pour chaque question posée, une seule des réponses proposées est exacte.
On demande bien sûr de justifier.
Pour chaque question posée, une seule des réponses proposées est exacte.
On demande bien sûr de justifier.
Question 1
Partie A
Pour les deux questions suivantes, on considère une fonction deux fois dérivable sur .
On donne ci-dessous le tableau de variation de .

Pour les deux questions suivantes, on considère une fonction deux fois dérivable sur .
On donne ci-dessous le tableau de variation de .

La fonction est :
- Croissante sur
- Décroissante sur
- Décroissante sur
- Croissante sur
- Croissante sur
- Décroissante sur
- Décroissante sur
- Croissante sur
Correction
La bonne réponse est b.
On va établir le tableau de signe de et on aura ainsi les variations de .
On remarque grâce au tableau de variation de que :
Ce qui donne :
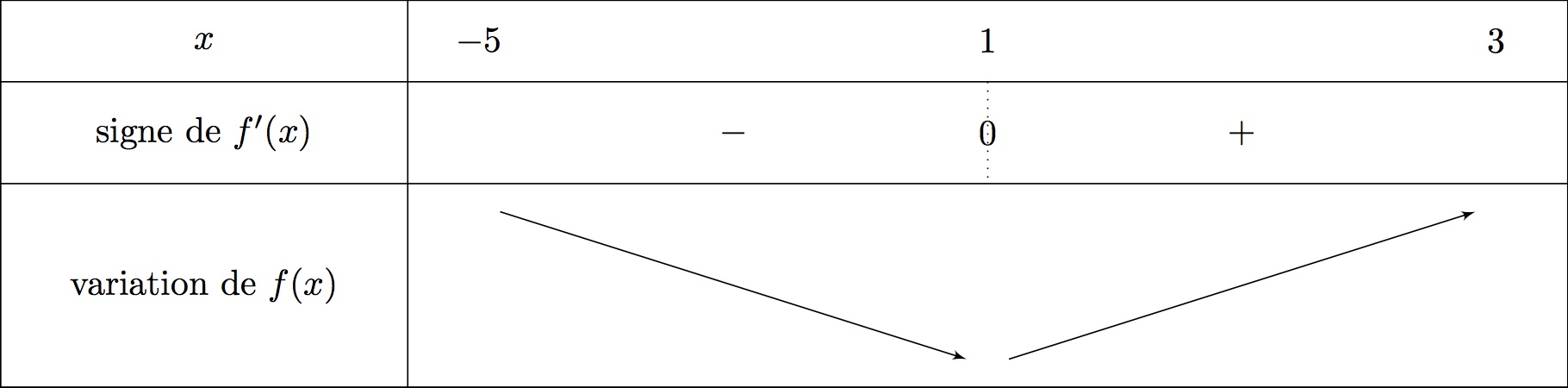
- Si est négative sur donc que est décroissante sur .
- Si est positive sur donc que est croissante sur .
On remarque grâce au tableau de variation de que :
- est négative sur donc que est décroissante sur .
- est positive sur donc que est croissante sur .
Ce qui donne :

Question 2
La fonction est :
- Convexe sur
- Concave sur
- Concave sur
- Convexe sur
- Convexe sur
- Concave sur
- Concave sur
- Convexe sur
Correction
La bonne réponse est b.
D'après le tableau de variation de , on en déduit :
est croissante alors est convexe sur
est décroissante alors est concave sur
- Si est croissante alors est convexe sur
- Si est décroissante alors est concave sur
est croissante alors est convexe sur
est décroissante alors est concave sur
Question 3
Partie B
Dans cette partie, il faudra répondre Vrai ou Faux mais bien sûr vous devez justifier.
On donne ci-dessous la courbe représentative de la dérivée d'une fonction définie sur .
On admet que la fonction est deux fois dérivable sur et on note sa dérivée seconde.
Les droites et sont tangentes à la courbe respectivement aux points d'abscisse et d'abscisse 1.
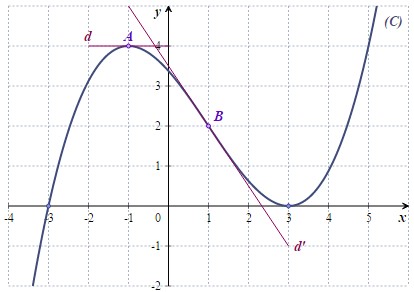
Dans cette partie, il faudra répondre Vrai ou Faux mais bien sûr vous devez justifier.
On donne ci-dessous la courbe représentative de la dérivée d'une fonction définie sur .
On admet que la fonction est deux fois dérivable sur et on note sa dérivée seconde.
Les droites et sont tangentes à la courbe respectivement aux points d'abscisse et d'abscisse 1.

Au point d'abscisse , la courbe représentative de la fonction admet un point d'inflexion.
Correction
La réponse est Vrai.
Nous disposons de la représentation graphique de .
Nous allons donc dresser le tableau de variation de qui nous indiquera ensuite le signe de la dérivée seconde .
Nous en déduirons donc les différents points d'inflexions.
Il vient alors :
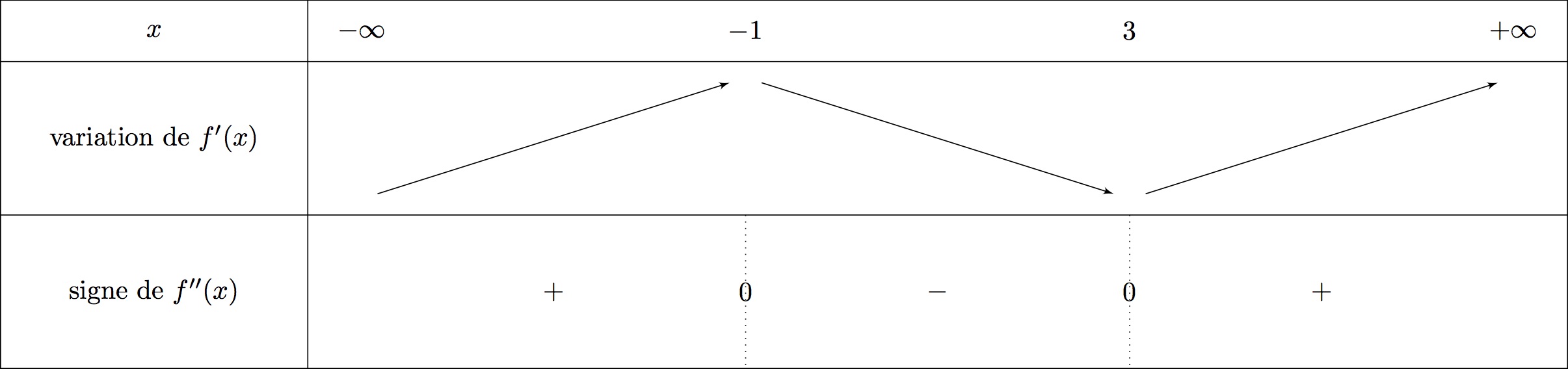 On voit que la signe de change de signe au point d'abscisse .
On voit que la signe de change de signe au point d'abscisse .
Il en résulte que la courbe, au point d'abscisse , la courbe représentative de la fonction admet un point d'inflexion.
Il en est de même pour l'abscisse
Nous disposons de la représentation graphique de .
Nous allons donc dresser le tableau de variation de qui nous indiquera ensuite le signe de la dérivée seconde .
Nous en déduirons donc les différents points d'inflexions.
Il vient alors :

Il en résulte que la courbe, au point d'abscisse , la courbe représentative de la fonction admet un point d'inflexion.
Il en est de même pour l'abscisse
Question 4
La courbe représentative de la fonction est croissante sur l'intervalle
Correction
La réponse est Faux.
Nous disposons de la représentation graphique de .
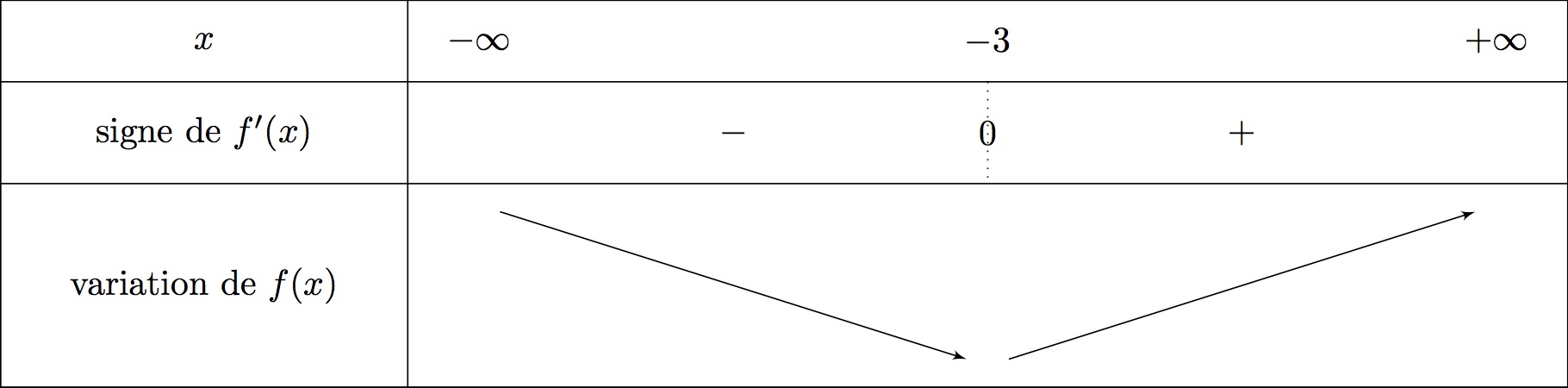 Nous allons donc dresser le tableau de signe de .
Nous allons donc dresser le tableau de signe de .
La courbe représentative de la fonction est décroissante sur l'intervalle
- Si est négative sur donc que est décroissante sur .
- Si est positive sur donc que est croissante sur .

La courbe représentative de la fonction est décroissante sur l'intervalle
Question 5
La courbe représentative de la fonction est concave sur l'intervalle .
Correction
La réponse est Vrai.
Nous disposons de la représentation graphique de .
Nous allons donc dresser le tableau de variation de qui nous indiquera ensuite le signe de la dérivée seconde .
On obtiendra ainsi la convexité de .
Il vient alors :
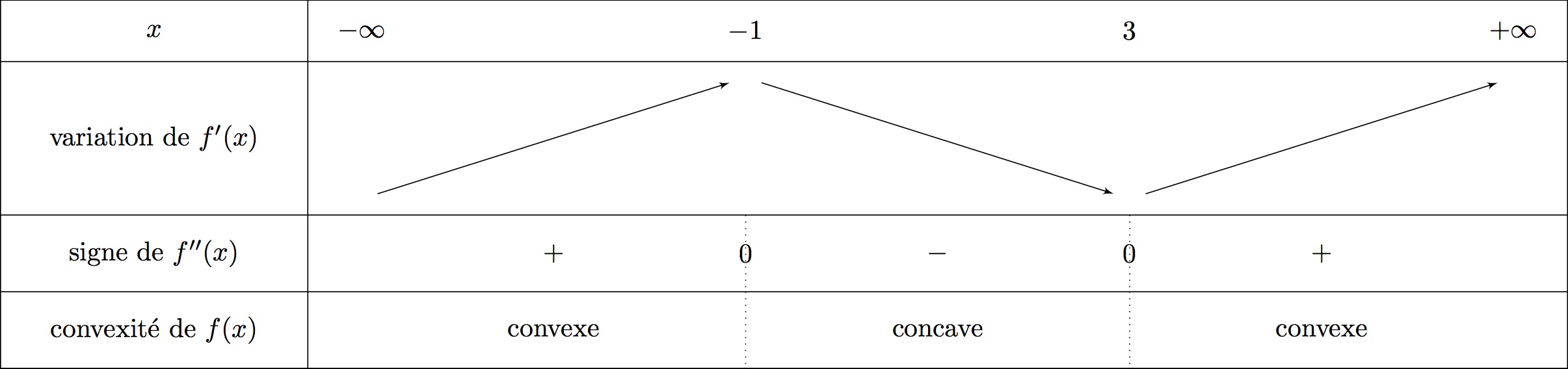
La courbe représentative de la fonction est bien concave sur l'intervalle .
Nous disposons de la représentation graphique de .
Nous allons donc dresser le tableau de variation de qui nous indiquera ensuite le signe de la dérivée seconde .
On obtiendra ainsi la convexité de .
Il vient alors :

La courbe représentative de la fonction est bien concave sur l'intervalle .
Question 6
Partie C
Dans cette partie, il faudra répondre Vrai ou Faux mais bien sûr vous devez justifier.
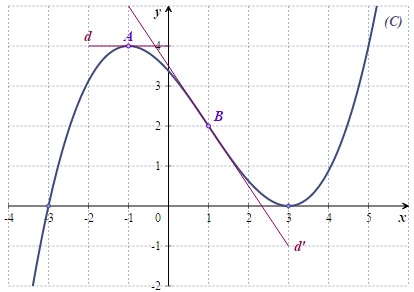
On donne ci-dessous la courbe représentative d'une fonction définie sur .
Dans cette partie, il faudra répondre Vrai ou Faux mais bien sûr vous devez justifier.
On donne ci-dessous la courbe représentative d'une fonction définie sur .

et
Correction
La proposition est Faux.
Pour déterminer la valeur de , on doit lire le coefficient directeur de la tangente au point d'abscisse .
Pour déterminer la valeur de , on doit lire le coefficient directeur de la tangente au point d'abscisse .
(cf. vidéo Lecture graphique et nombre dérivée).
donc
Pour déterminer la valeur de , on doit lire le coefficient directeur de la tangente au point d'abscisse .
car la tangente est horizontale
Pour déterminer la valeur de , on doit lire le coefficient directeur de la tangente au point d'abscisse .
(cf. vidéo Lecture graphique et nombre dérivée).
donc
Question 7
Le signe de est négatif.
Correction
La proposition est Faux.
Nous disposons de la représentation graphique de .
Nous allons donc dresser le tableau de variation de et nous obtiendrons le signe de .
Il vient alors que :

Sur l'intervalle la fonction est croissante il en résulte donc est positive sur .
Ainsi le signe de est positif.
- Si est décroissante sur alors est négative sur
- Si est croissante sur alors est positive sur
Nous allons donc dresser le tableau de variation de et nous obtiendrons le signe de .
Il vient alors que :

Sur l'intervalle la fonction est croissante il en résulte donc est positive sur .
Ainsi le signe de est positif.
Question 8
Un encadrement de par des entiers naturels successifs est : .
Correction
La proposition est Faux
La fonction est positive sur donc l'intégrale est positive et est égale à l'aire sous la courbe et l'axe des abscisses et délimité par les droites verticales et .
Il suffit de compter les nombres de carreaux sous la courbe et l'axe des abscisses et délimité par les droites verticales et .
Il y a plus d'un carreau mais moins de deux carreaux, donc
La fonction est positive sur donc l'intégrale est positive et est égale à l'aire sous la courbe et l'axe des abscisses et délimité par les droites verticales et .
Il suffit de compter les nombres de carreaux sous la courbe et l'axe des abscisses et délimité par les droites verticales et .
Il y a plus d'un carreau mais moins de deux carreaux, donc
Question 9
Partie D.
une seule des réponses proposées est exacte.
une seule des réponses proposées est exacte.
, , sont les courbes représentatives d’une fonction , de sa dérivée et d’une de ses primitives .
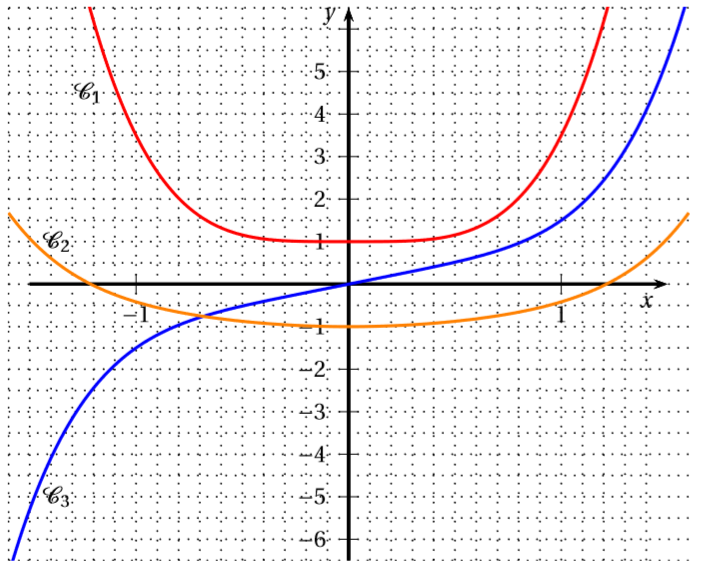 , , sont respectivement les courbes représentatives de :
, , sont respectivement les courbes représentatives de :
- , et
- , et
- , et
- , et

- , et
- , et
- , et
- , et
Correction
La bonne réponse est .
D'après le graphique, nous allons considérer travailler sur l'intervalle .
On observe que :
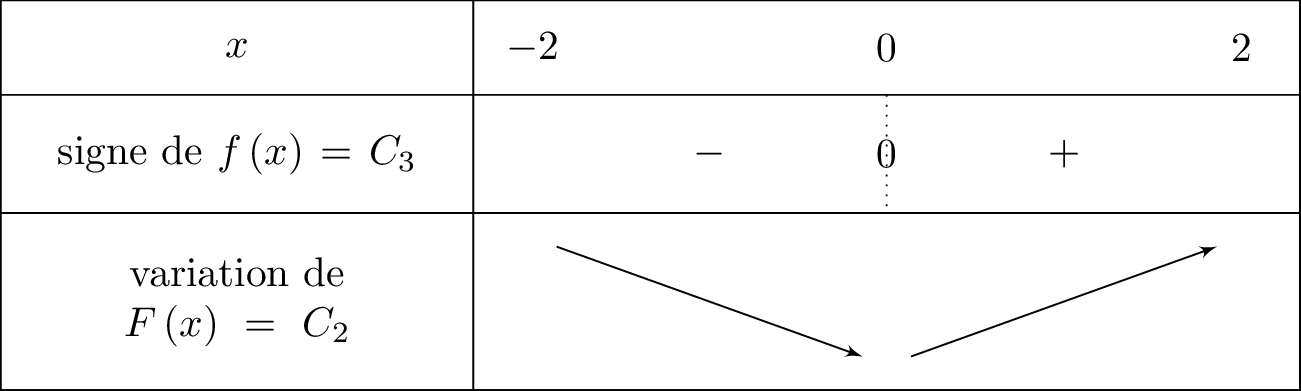
D'après le graphique, nous allons considérer travailler sur l'intervalle .
On observe que :
- Si est négative sur alors est décroissante sur
- Si est positive sur alors est croissante sur

- Lorsque est positive sur alors est croissante sur
- Lorsque est négative sur alors est décroissante sur
