🔴 Lives #BAC2024
À partir du 12 mai, révise le bac avec nous sur YouTube tous les soirs à 19h30 ! Découvrir la chaîne →
Géométrie repérée : équation de droite, vecteur normal et équation de cercle
Exercices types : ème partie - Exercice 1
10 min
15
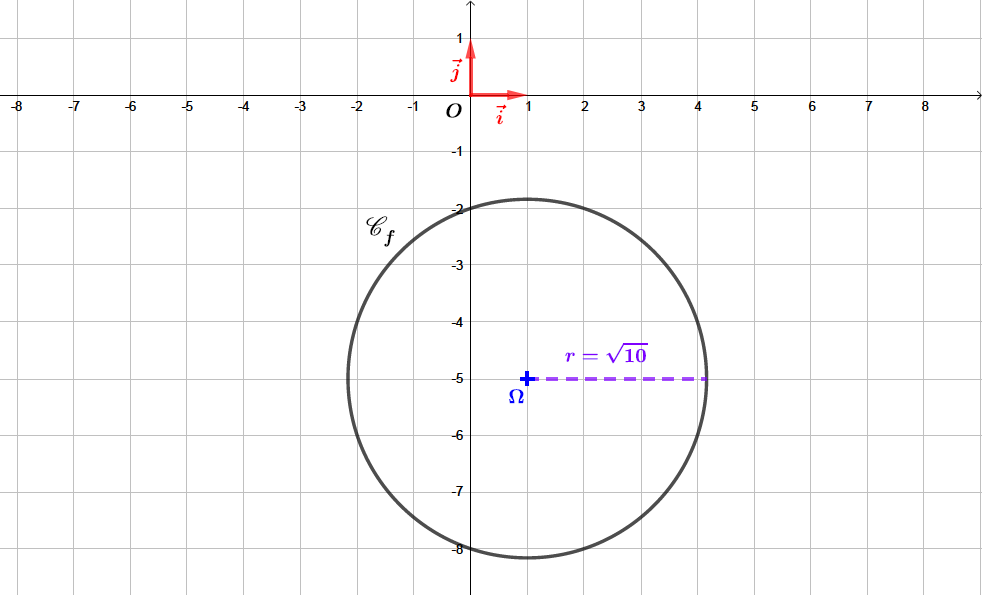
On donne l'équation d'un cercle de la forme
Question 1
Tracer la représentation graphique de dans un repère
Correction
- L’équation cartésienne d'un cercle de centre de coordonnée et de rayon est donnée par la formule :
On peut donc l'écrire également :
Avec
On peut donc conclure que est l'équation d'un cercle de centre de coordonnée et de rayon .
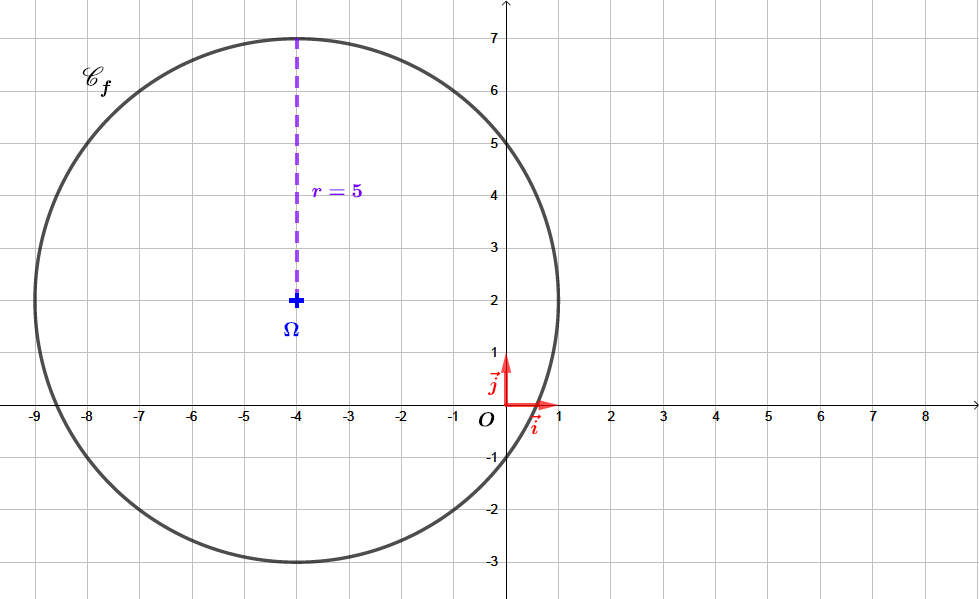
Question 2
On donne l'équation d'un cercle de la forme
Tracer la représentation graphique de dans un repère
Correction
- L’équation cartésienne d'un cercle de centre de coordonnée et de rayon est donnée par la formule :
On peut donc l'écrire également :
Avec
On peut donc conclure que est l'équation d'un cercle de centre de coordonnée et de rayon .
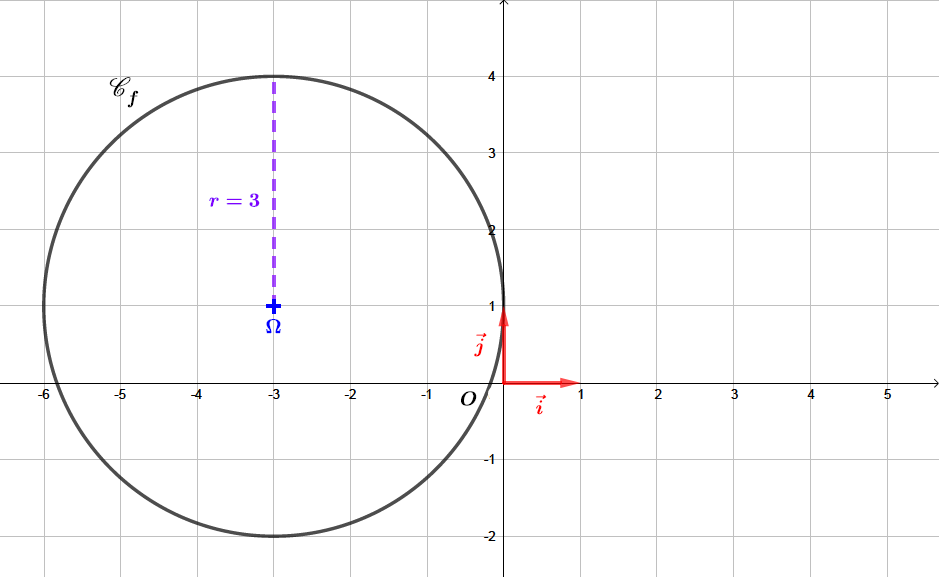
Question 3
On donne l'équation d'un cercle de la forme
Tracer la représentation graphique de dans un repère
Correction
- L’équation cartésienne d'un cercle de centre de coordonnée et de rayon est donnée par la formule :
On peut donc l'écrire également :
Avec
On peut donc conclure que est l'équation d'un cercle de centre de coordonnée et de rayon .
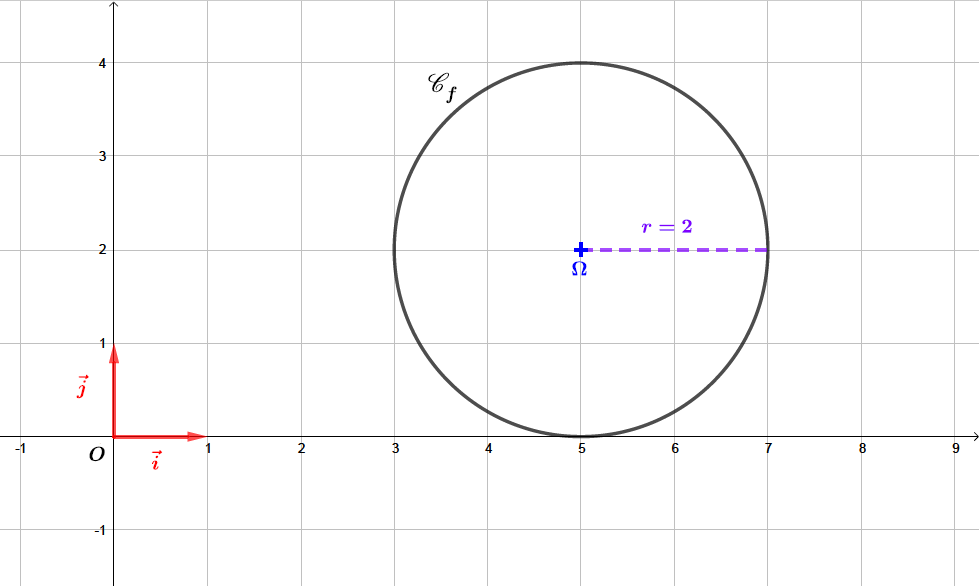
Question 4
On donne l'équation d'un cercle de la forme
Tracer la représentation graphique de dans un repère
Correction
- L’équation cartésienne d'un cercle de centre de coordonnée et de rayon est donnée par la formule :
On peut donc l'écrire également :
Avec
On peut donc conclure que est l'équation d'un cercle de centre de coordonnée et de rayon .