Variations des fonctions associées
Variation des fonctions de référence - Exercice 1
1 min
0
Déterminer le tableau de variation des fonctions suivantes sur l'intervalle considéré.
Question 1
;
Correction
Si alors il s'agit d'une parabole dont le sommet est .
- Si la fonction est décroissante sur et croissante sur
- Si la fonction est croissante sur et décroissante sur
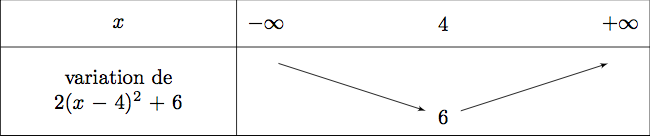
Nous avons ici : ; et .
Comme la fonction est décroissante sur et croissante sur .
On en déduit le tableau de variation suivant :
Question 2
;
Correction
Si alors il s'agit d'une parabole dont le sommet est .
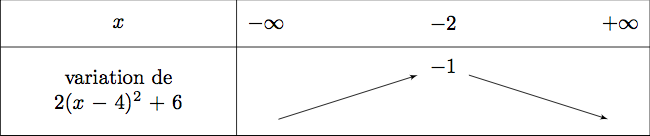
Nous avons ici : ; et . - Si la fonction est décroissante sur et croissante sur
- Si la fonction est croissante sur et décroissante sur
Comme la fonction est croissante sur et décroissante sur .
On en déduit le tableau de variation suivant :
Question 3
;
Correction
On décompose la fonction en avec .
est une fonction affine croissante car le coefficient directeur .
De plus, la fonction est de signe constant sur l'intervalle comme le montre le tableau de signe ci-dessous :
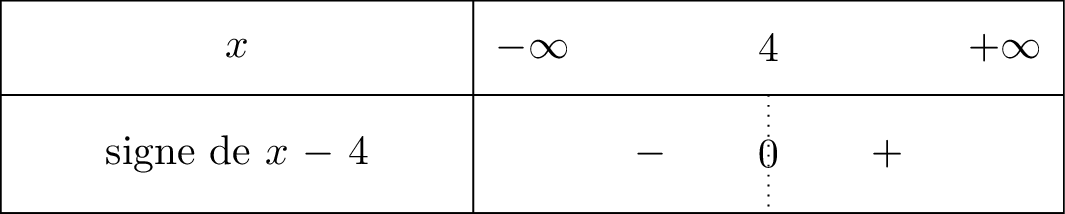
Comme les fonctions et ont des sens de variations contraires, alors la fonction c'est à dire est décroissante sur l'intervalle .
On résume cela dans le tableau de variation ci-dessous :
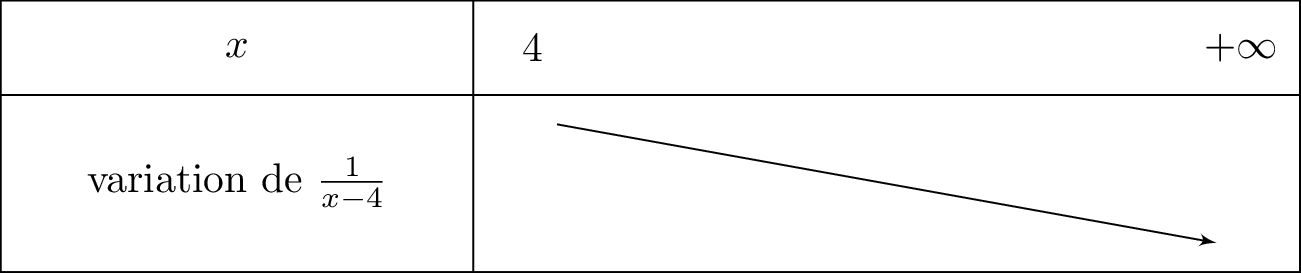
est une fonction affine croissante car le coefficient directeur .
De plus, la fonction est de signe constant sur l'intervalle comme le montre le tableau de signe ci-dessous :

Comme les fonctions et ont des sens de variations contraires, alors la fonction c'est à dire est décroissante sur l'intervalle .
On résume cela dans le tableau de variation ci-dessous :

Question 4
;
Correction
On décompose la fonction en avec .
est une fonction affine décroissante car le coefficient directeur .
De plus, la fonction est de signe constant sur l'intervalle comme le montre le tableau de signe ci-dessous :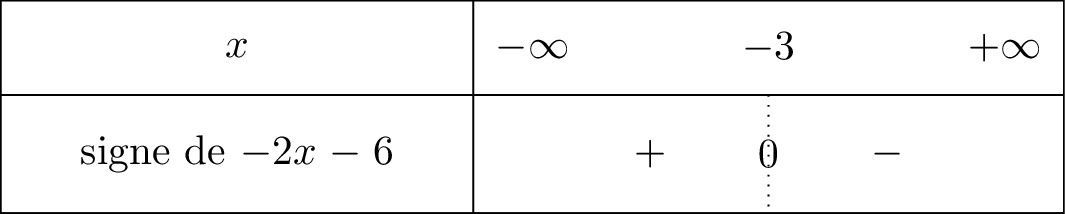 Comme les fonctions et ont des sens de variations contraires, alors la fonction c'est à dire est croissante sur l'intervalle .
Comme les fonctions et ont des sens de variations contraires, alors la fonction c'est à dire est croissante sur l'intervalle .
On résume cela dans le tableau de variation ci-dessous :
est une fonction affine décroissante car le coefficient directeur .
De plus, la fonction est de signe constant sur l'intervalle comme le montre le tableau de signe ci-dessous :

On résume cela dans le tableau de variation ci-dessous :

Question 5
;
Correction
- Si alors .
- Si alors .
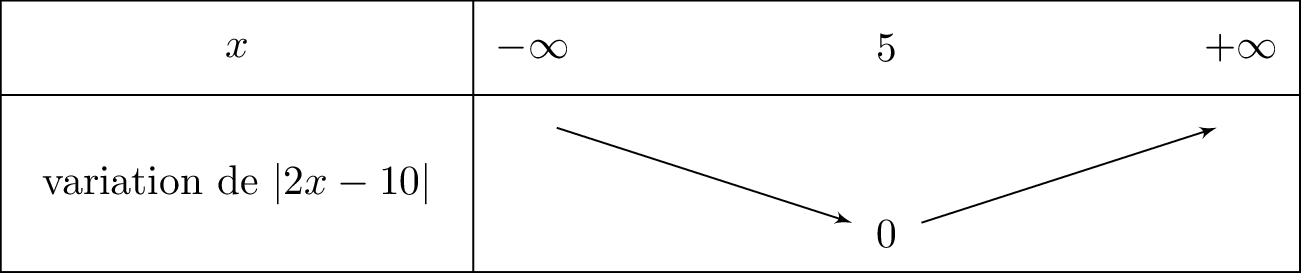
On commence par étudier le signe . Il s'agit d'une fonction affine.
équivaut à . On a donc :

si alors . Il en résulte que : . La fonction affine est croissante car le coefficient directeur est négatif.
Finalement :
Question 6
;
Correction
- Si alors .
- Si alors .
On commence par étudier le signe . Il s'agit d'une fonction affine.
équivaut à . On a donc :
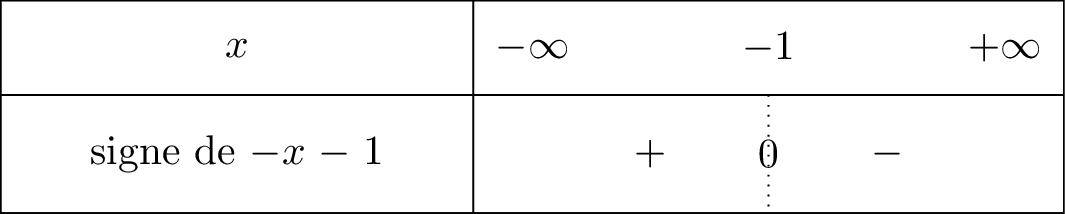
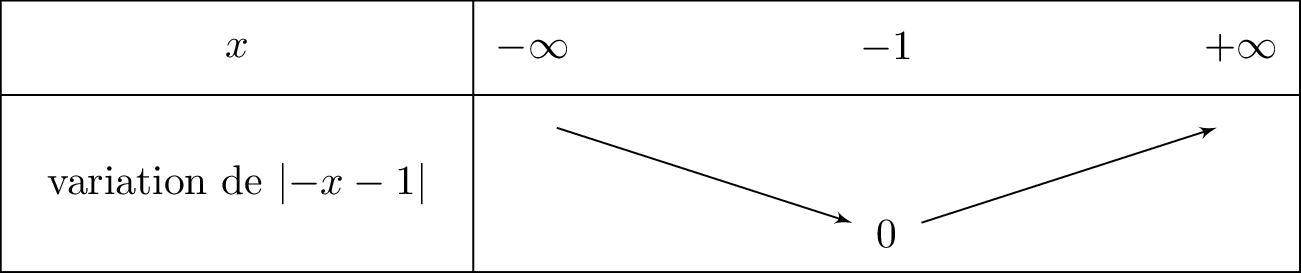
si alors . Il en résulte que : . La fonction affine est croissante car le coefficient directeur est positif.
Finalement :
Question 7
;
Correction
Pour les variations, on décompose la fonction en avec .
La fonction est une fonction affine de coefficient directeur . La fonction est donc croissante sur .
Comme les fonctions et ont les mêmes variations, la fonction est croissante sur .
La fonction est une fonction affine de coefficient directeur . La fonction est donc croissante sur .
- Racine carré
- Soit une fonction positive sur , alors les fonctions et ont les mêmes variations.
Question 8
;
Correction
Pour les variations, on décompose la fonction en avec .
La fonction est une fonction affine de coefficient directeur . La fonction est donc décroissante sur .
Comme les fonctions et ont les mêmes variations, la fonction est décroissante sur .
La fonction est une fonction affine de coefficient directeur . La fonction est donc décroissante sur .
- Racine carré
- Soit une fonction positive sur , alors les fonctions et ont les mêmes variations.
Question 9
;
Correction
On décompose la fonction en avec .
est une fonction affine croissante car le coefficient directeur .
De plus, la fonction est de signe constant sur l'intervalle comme le montre le tableau de signe ci-dessous :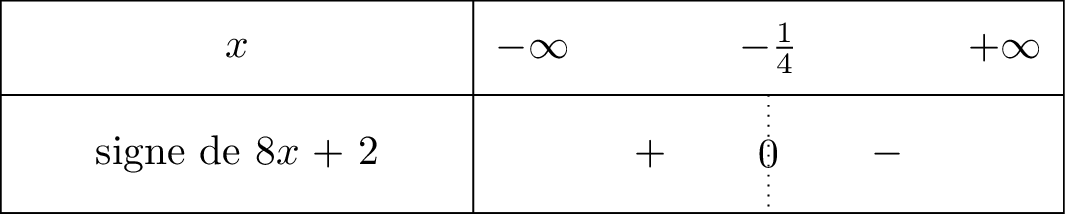 Comme les fonctions et ont des sens de variations contraires, alors la fonction c'est à dire est décroissante sur l'intervalle .
Comme les fonctions et ont des sens de variations contraires, alors la fonction c'est à dire est décroissante sur l'intervalle .
On résume cela dans le tableau de variation ci-dessous :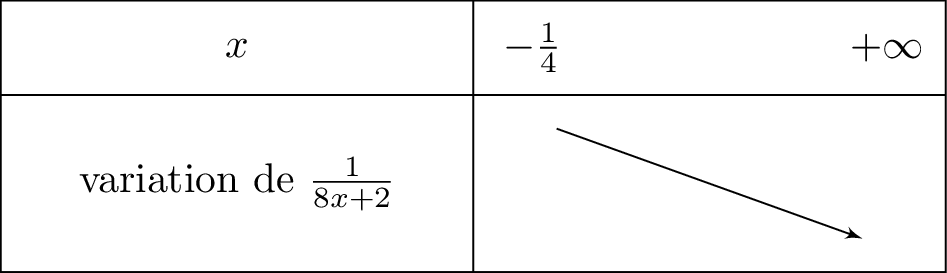
est une fonction affine croissante car le coefficient directeur .
De plus, la fonction est de signe constant sur l'intervalle comme le montre le tableau de signe ci-dessous :

On résume cela dans le tableau de variation ci-dessous :
