Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Sujet inédit 1 - Exercice 1

1 min
0
Question 1
Lors d’un meeting aérien, un avion passe devant des spectateurs immobiles à une vitesse v=720v=720 km.h−1km.h^{-1} selon le schéma ci-dessous en émettant un son de fréquence fe=1000f_{e}=1000 Hz se propageant à la célérité 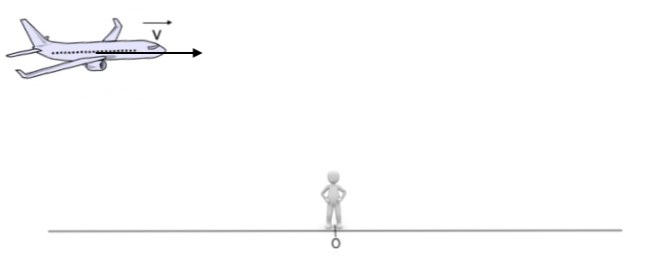c=340c=340 m.s−1m.s^{-1}

La célérité d’un son dépend de sa fréquence.

Correction
La proposition est FAUSSE.
La vitesse d'un son ne dépend que du milieu de propagation.
  • Un ultrason, un infrason, un son audible, ont des fréquences différentes, mais dans l'air ils se propagent tous à la même vitesse de 340340 m.s−1^{-1} .
    • Question 2

    A l’approche de l’avion les spectateurs perçoivent un son plus grave que celui émis par l’avion.

    Correction
    La proposition est FAUSSE.
    La source se rapproche des spectateurs, donc devant le nez de l'avion les ondes sonores ont des longueurs d'onde plus petites. L'avion tend à rattraper les ondes qu'il crée.
    Or : V=f×λV=f\times \lambda et VV est constant pour un son dans l'air (340340 m.s−1^{-1}). Donc si λ\lambda diminue alors ff augmente, si ff augmente le son perçu sera plus aigu.
    Question 3
    On rappelle l'énoncé de l'exercice :
    Lors d’un meeting aérien, un avion passe devant des spectateurs immobiles à une vitesse v=720v=720 km.h−1km.h^{-1} selon le schéma ci-dessous en émettant un son de fréquence fe=1000f_{e}=1000 Hz se propageant à la célérité c=340c=340 m.s−1m.s^{-1}

    En utilisant la relation traduisant l’effet Doppler pour un émetteur s’approchant d’un récepteur fp=cc−v⋅fef_{p} =\frac{c}{c-v} \cdot f_{e}
    La fréquence perçue fpf_{p} à l'approche est de l'ordre de fp≈2500f_{p}\approx2500 Hz .

    Correction
    La proposition est VRAIE.
    On a : fp=cc−v⋅fef_{p} =\frac{c}{c-v} \cdot f_{e}.
    Or c=340c=340 m.s−1m.s^{-1} . De plus, v=720v=720 km.h−1km.h^{-1} ce qui donne v=7203,6=200v=\frac{720}{3,6}=200 m.s−1^{-1}.
    Il vient alors que :
    fp=340340−200×1000f_{p} =\frac{340}{340-200} \times 1000
    fp=340140×1000f_{p} =\frac{340}{140} \times 1000 . Or : 340140≈2,5\frac{340}{140} \approx 2,5
    Ainsi :
    fp≈2,5×1000f_{p} \approx 2,5\times 1000
    fp≈2500f_{p} \approx 2500 Hz
    Question 4
    Le son perçu est enregistré à l’aide d’une carte d’acquisition reliée à un ordinateur.

    Le signal obtenu est un signal périodique mais non sinusoïdal. Le son enregistré est pur.

    Correction
    La proposition est FAUSSE.
    Définition du cours :
    Un son périodique mais non-sinusoidal est complexe.
    Question 5

    L’intensité sonore mesurée par un spectateur est de 10−610^{-6} W.m2W.m^{2}. La valeur du niveau sonore est donc ( avec I0=10−12I_{0}=10^{-12} W.m2W.m^{2} ) L=6L=6 dBdB .

    Correction
    La proposition est FAUSSE.
    Définition du cours :
  • On appelle niveau sonore, le nombre LL, exprimé en décibel dB, défini par : L=10log⁡(II0)L=10\log \left(\frac{I}{I_{0} } \right) .
    Avec II l'intensité mesurée en W.m−2W.m^{-2} ; LL le niveau sonore en dB et I0I_{0} intensité sonore de référence I0=1⋅10−12I_{0}=1\cdot 10^{-12} W.m−2W.m^{-2}
    • Ainsi :
    L=10log⁡(II0)L=10\log \left(\frac{I}{I_{0} } \right) équivaut successivement à :
    L=10log⁡(1⋅10−61⋅10−12)L=10\log \left(\frac{1\cdot 10^{-6}}{1\cdot 10^{-12} } \right)
    L=10log⁡(106)L=10\log \left(10^{6} \right)
    Définition du cours :
  • log⁡(10x)=x\log \left(10^{x} \right)=x
    • L=10×6L=10\times6
    L=60L=60 dBdB

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.