Concours Avenir 2018 - Avenir - Concours

Question 1

Thomas Pesquet décolle le

17

novembre

2016

à

20

h

20

TUC à bord d'un vaisseau Soyouz. Le Soyouz MS-03 est placé en orbite par une fusée Soyouz tirée depuis le cosmodrome de Baïkonour au Kazakhstan.
On étudiera dans un premier temps la phase de décollage de la fusée, ensuite son mouvement une fois les réacteurs éteints et enfin le mouvement de la station spatiale sur son orbite autour de la Terre.
La photographie suivante représente la fusée sur le tir de lancement.

Donnée : intensité de pesanteur

g=9,8

N.kg

^{-1}

On étudie le décollage de la fusée par rapport au référentiel terrestre. Durant son décollage, grâce à ses moteurs qui éjectent des gaz, la fusée acquiert une accélération qui lui permet de décoller.
On désignera par

m_{f}

la masse de la fusée,

m_{g}

la masse des gaz éjectés,

\vec{V_{f}}

la vitesse de la fusée et

\vec{V_{g}}

la vitesse des gaz.
Le système {fusée + gaz} sera considéré comme pseudo-isolé.

Afin de pouvoir décoller et quitter le sol terrestre, la fusée doit acquérir une accélération de norme :
nulle
inférieure à $g$
égale à $g$
supérieur à $g$

Correction

La bonne réponse est d.
Une force en physique est équivalente au produit d'une masse par une accélération :

\text{FORCE}=\text{MASSE}\times\text{ACCELERATION}

ou de façon plus réduite :

F=m\times a

.
Or, pour que la fusée décolle, il faut une force

F

supérieure à son poids

P

dirigée vers le haut.
Ainsi :

F>P

mais comme

P=mg

, il en résulte que :

m\times a>mg

et cela nous donne

a>g

.

Question 2

Au moment du décollage, la quantité de mouvement du système {fusée + gaz}, $\vec{p}$ est :
$\vec{p}=\vec{0}$
$\vec{p}=m_{f} \cdot \vec{V_{f}} \left(t\right)$
$\vec{p}=m_{g} \cdot \vec{V_{g}} \left(t\right)$
$\vec{p}=m_{f} \cdot \vec{V_{f}} \left(t\right)-m_{g} \cdot \vec{V_{g}} \left(t\right)$

Correction

La bonne réponse est a.
La quantité de mouvement d'un système pseudo-isolé est constante.
Ici, avant le décollage, le système subit son poids et la réaction du sol. Le système est immobile ( il n'est pas encore en mouvement ) donc la vitesse de la fusée est nulle et de ce fait sa quantité de mouvement est nulle.

Question 3

Au cours du décollage, la quantité de mouvement du système {fusée + gaz} :
diminue
reste constante
augmente
est nulle

Correction

La bonne réponse est b.

Définition du cours :

Un système pseudo-isolé a une quantité de mouvement constante.

Question 4

Lorsque les réacteurs s’éteignent, la fusée se situe à une altitude

h

du sol terrestre et a une vitesse

\vec{V_{0}}

de coordonnées

\left(V_{Ox}, V_{Oy}\right)

dans le repère

\left(Oxy\right)

. Durant cette phase, la fusée n’est soumise qu’à son poids. Les frottements avec l’air seront négligés. La fusée sera assimilée à un corps ponctuel noté

f

.

Les coordonnées de la vitesse initiale $\vec{V_{0}}$ dans le repère $\left(Oxy\right)$ sont :
$\left(V_{0} ;0\right)$
$\left(0;V_{0} \right)$
$\left(V_{0} \cdot \sin \alpha ;V_{0} \cdot \cos \alpha \right)$
$\left(V_{0} \cdot \cos \alpha ;V_{0} \cdot \sin \alpha \right)$

Correction

La bonne réponse est c.

Le vecteur

\vec{V_{0}}

a deux composantes : ce sont les deux projections orthogonales sur les droites

\left(Ox\right)

et

\left(Oy\right)

.
La composante sur

\left(Oy\right)

est le segment qui représente le coté adjacent du triangle rectangle dont

V_{0}

est l'hypoténuse, et la composante sur

\left(Ox\right)

est le segment qui représente le coté opposé de ce triangle.
Il en résulte donc que

\vec{V_{0}}

a comme composante

\left(V_{0} \cdot \sin \alpha ;V_{0} \cdot \cos \alpha \right)

Question 5

Pour déterminer l’accélération, on utilisera ici :
la $1$ ^ère loi de Newton
la $2$ ^ème loi de Newton
la $2$ ^ème loi de Kepler
la $3$ ^ème loi de Kepler

Correction

La bonne réponse est b.
L'accélération est la base des études dynamiques. C'est la

2

^ème loi de Newton qui en est l'expression :

\sum \vec{F_{\text{ext}}}=m\times \vec{a}

Question 6

L’accélération de la fusée pendant cette phase a pour expression :
$\vec{a}=\vec{g}$
$\vec{a}=-\vec{g}$
$\vec{a}=\vec{P}$
$\vec{a}=-\vec{P}$

Correction

La bonne réponse est a.

La fusée n'est soumise qu'à son poids

\vec{P}

. Donc, si on lui applique la

2

^ème loi de Newton

\sum \vec{F_{\text{ext}}}=m\times \vec{a}

, on aura :

\vec{P}=m\times \vec{a}

m\times \vec{g}=m\times \vec{a}

\vec{g}= \vec{a}

Question 7

Pour obtenir l’expression des coordonnées de la fusée en fonction du temps, il faut :
dériver l’accélération
dériver la dérivée de l’accélération
obtenir la primitive de l’accélération
obtenir la primitive de la primitive de l’accélération

Correction

La bonne réponse est d.
Quand on part de la position

\vec{OM}

, on dérive par rapport au temps pour trouver la vitesse

\vec{v}=\frac{d\vec{OM}}{dt}

et même chose pour trouver l'accélération

\vec{a}=\frac{d\vec{v}}{dt}

.
Quand on part de l'accélération, il faut donc intégrer pour trouver la vitesse puis faire une deuxième primitive pour trouver la position.

Question 8

Les coordonnées de la vitesse $\vec{V}$ de la fusée en fonction du temps sont :
$V_{x} \left(t\right)=V_{0} \cdot \sin \alpha$ ; $V_{y} \left(t\right)=-gt+V_{0} \cdot \cos \alpha$
$V_{x} \left(t\right)=V_{0} \cdot \sin \alpha$ ; $V_{y} \left(t\right)=gt+V_{0} \cdot \cos \alpha$
$V_{x} \left(t\right)=V_{0} \cdot \cos \alpha$ ; $V_{y} \left(t\right)=-gt+V_{0} \cdot \sin \alpha$
$V_{x} \left(t\right)=V_{0} \cdot \cos \alpha$ ; $V_{y} \left(t\right)=-gt-V_{0} \cdot \sin \alpha$

Correction

La bonne réponse est a.

L'accélération

\vec{a}

de la fusée est

\vec{g}

. Or le vecteur

\vec{g}

est dirigé vers le bas, donc sans le sens inverse de l'axe

\left(Oy\right)

.
Le vecteur

\vec{g}

a pour coordonnées

\vec{g} \left(\begin{array}{c} {g_{x}\left(t\right) =0} \\ {g_{y}\left(t\right) =-g } \end{array}\right)

.
Pour trouver la vitesse, on cherche la primitive de

\vec{g}

. Il vient alors que :

\vec{V} \left(\begin{array}{c} {V_{x}\left(t\right) =V_{0}\sin \left(\alpha \right)} \\ {V_{y}\left(t\right) =-gt+V_{0}\cos \left(\alpha \right) } \end{array}\right)

Question 9

Les coordonnées de la position $\vec{OM}$ de la fusée en fonction du temps sont :
$x\left(t\right)=V_{0} \cdot \sin \alpha \cdot t$ ; $y\left(t\right)=\frac{1}{2} gt^{2} +V_{0} \cdot \cos \alpha \cdot t+h$
$x\left(t\right)=V_{0} \cdot \sin \alpha \cdot t$ ; $y\left(t\right)=-\frac{1}{2} gt^{2} +V_{0} \cdot \cos \alpha \cdot t+h$
$x\left(t\right)=V_{0} \cdot \cos \alpha \cdot t$ ; $y\left(t\right)=-\frac{1}{2} gt^{2} +V_{0} \cdot \cos \alpha \cdot t+h$
$x\left(t\right)=V_{0} \cdot \cos \alpha \cdot t$ ; $y\left(t\right)=\frac{1}{2} gt^{2} +V_{0} \cdot \cos \alpha \cdot t+h$

Correction

La bonne réponse est b.

On cherche la primitive de

\vec{V}

qui est la position

\vec{OM}

de la fusée.
D'après la question précédente, nous savons que :

\vec{V} \left(\begin{array}{c} {V_{x}\left(t\right) =V_{0}\sin \left(\alpha \right)} \\ {V_{y}\left(t\right) =-gt+V_{0}\cos \left(\alpha \right) } \end{array}\right)

On intègre, il vient que :

\vec{OM} \left(\begin{array}{c} {x\left(t\right) =V_{0}\sin \left(\alpha \right)\times t} \\ {y\left(t\right) =-\frac{1}{2}gt^{2}+V_{0}\cos \left(\alpha \right)\times t+h } \end{array}\right)

Question 10

Soyouz MS-03 est maintenant arrimée à la Station Spatiale Internationale ISS dont nous allons étudier ici quelques paramètres. On supposera que la Station Spatiale Internationale ne subit que l’attraction gravitationnelle de la Terre.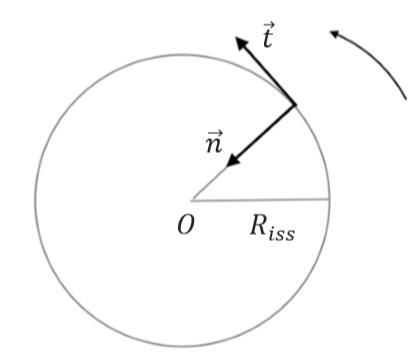

Données : Expression de l’accélération de la station dans la base de Frenet :

\vec{a}=\frac{dv}{dt} \vec{t}+\frac{v^{2} }{R_{\text{iss}} } \vec{n}

\vec{a}

: accélération de la Station Spatiale Internationale

v

: norme de la vitesse de la Station Spatiale Internationale

R_{\text{iss}}

: distance entre la Station Spatiale Internationale et la Terre

\vec{t}

et

\vec{n}

: vecteurs unitaires de la base de Frenet

Pour étudier la trajectoire de la Station Spatiale Internationale ISS (masse $M_{S}$ ) autour de la Terre (masse $M_{T}$ ), il faut se placer dans le référentiel :
héliocentrique
géocentrique
terrestre
de Kepler

Correction

La bonne réponse est b.
La station tourne autour de la Terre, ne touche pas sa surface donc le référentiel adapté est le référentiel géocentrique.

Question 11

Une des lois de Kepler permet de relier la période d’un Astre sur son orbite au rayon de celle-ci. Il s’agit :
de la $1$ ^ère loi de Kepler
de la $2$ ^ème loi de Kepler
de la loi des aires
de la $3$ ^ème loi de Kepler

Correction

La bonne réponse est d.
La

3

^ème loi de Kepler relie la période

T

d'un astre au rayon

R

de son orbite. Nous avons :

\frac{T^{2}}{R^{3}}=\text{constante}

Question 12

La période $T_{\text{iss}}$ de révolution de la Station Spatiale Internationale en fonction de rayon $R_{\text{iss}}$ est :
$\frac{R_{\text{iss}}^{3} }{T_{\text{iss}}^{2} } =\frac{4\pi ^{2} }{GM_{T} }$
$\frac{R_{\text{iss}}^{2} }{T_{\text{iss}}^{3} } =\frac{4\pi ^{2} }{GM_{S} }$
$\frac{T_{\text{iss}}^{3} }{R_{\text{iss}}^{2} } =\frac{4\pi ^{2} }{GM_{S} }$
$\frac{T_{\text{iss}}^{2} }{R_{\text{iss}}^{3} } =\frac{4\pi ^{2} }{GM_{T} }$

Correction

La bonne réponse est d.
D'après la question précédente, la

3

^ème loi de Kepler relie la période

T

d'un astre au rayon

R

de son orbite.
Nous avons :

\frac{T^{2}}{R^{3}}=\text{constante}

Pour calculer la constante, il faut savoir autour de quoi l'objet tourne. Ici, il s'agit de la Terre, donc :

\frac{T_{\text{iss}}^{2} }{R_{\text{iss}}^{3} } =\frac{4\pi ^{2} }{GM_{T} } =\text{constante}

La valeur de la constante change en fonction de l'objet autour duquel tourne notre objet satellite.

Question 13

En doublant la distance entre la Station Spatiale Internationale et la Terre, la période de révolution de la station sera :
multipliée par $2$
multipliée par $\sqrt{8}$
multipliée par $4$
multipliée par $8$

Correction

La bonne réponse est b.
Soit

R_{1}

la distance Terre/ISS. La période correspondante est

\frac{T_{1}^{2}}{R_{1}^{3}}=\text{constante}

. Si on double la distance :

2\times R_{1}=R_{2}

, la période devient

\frac{T_{2}^{2}}{R_{2}^{3}}=\text{constante}

.
Ainsi :

\frac{T_{1}^{2}}{R_{1}^{3}}=\frac{T_{2}^{2}}{R_{2}^{3}}

. Or ,

2\times R_{1}=R_{2}

. Il vient que :

\frac{T_{1}^{2} }{R_{1}^{3} } =\frac{T_{2}^{2} }{\left(2R_{1} \right)^{3} }

\frac{T_{1}^{2} }{R_{1}^{3} } =\frac{T_{2}^{2} }{8R_{1}^{3} }

\frac{T_{1}^{2} }{R_{1}^{3} } \times 8R_{1}^{3} =T_{2}^{2}

T_{2}^{2} =\frac{T_{1}^{2} }{R_{1}^{3} } \times 8R_{1}^{3}

T_{2}^{2} =8T_{1}^{2}

T_{2} =\sqrt{8T_{1}^{2} }

T_{2} =\sqrt{8} T_{1}

Question 14

L’expression de la force subie par la Station Spatiale Internationale est :
$\vec{F}=-\frac{GM_{T} M_{S} }{R_{\text{iss}} } \vec{n}$
$\vec{F}=-\frac{GM_{T} M_{S} }{\left(R_{\text{iss}} \right)^{2} } \vec{n}$
$\vec{F}=\frac{GM_{T} M_{S} }{R_{\text{iss}} } \vec{n}$
$\vec{F}=\frac{GM_{T} M_{S} }{\left(R_{\text{iss}} \right)^{2} } \vec{n}$

Correction

La bonne réponse est d.
La force que subit l'ISS est dirigée de l'ISS vers la Terre. C'est la Terre qui attire à elle l'ISS. Donc cette force est dans le même sens que

\vec{n}

.
Soit :

\vec{F}=\frac{GM_{T} M_{S} }{\left(R_{\text{iss}} \right)^{2} } \vec{n}

Question 15

L’accélération de la station est :
centripète
centrifuge
tangente à la trajectoire
nulle

Correction

La bonne réponse est a.
L'accélération est dirigée de l'ISS vers la terre, car la Terre attire l'ISS. Donc l'accélération est bien dirigé vers le centre de la Terre, elle est centripète.

Question 16

En utilisant la $2$ ^ème loi de Newton et l’expression de l’accélération de la station dans la base de Frenet, on obtient l’expression suivante de la norme de la vitesse de la Station autour de la Terre :
$V=\frac{GM{}_{T} }{R_{\text{iss}} }$
$V=\frac{GM_{T} }{\left(R_{\text{iss}} \right)^{2} }$
$V=\sqrt{\frac{GM{}_{T} }{R_{\text{iss}} } }$
$V=\sqrt{\frac{GM_{T} }{\left(R_{\text{iss}} \right)^{2} } }$

Correction

La bonne réponse est c.
D'après la question

14

, on sait que :

\vec{F}=\frac{GM_{T} M_{S} }{\left(R_{\text{iss}} \right)^{2} } \vec{n}

La

2

^ème loi de Newton est :

\sum \vec{F_{\text{ext}}}=m\times \vec{a}

.
L'accélération de l'ISS est uniquement suivant

\vec{n}

, car elle est centripète. On a donc :

\vec{a}=\frac{V^{2}}{R_{\text{iss}}}\vec{n}

.
Ainsi :

\sum \vec{F_{\text{ext}}}=\frac{GM_{T} M_{\text{iss}}}{\left(R_{\text{iss}} \right)^{2} } \vec{n}=M_{\text{iss}}\times \vec{a}=M_{\text{iss}}\times \frac{V^{2}}{R_{\text{iss}}}\vec{n}

On simplifie par

M_{\text{iss}}

, il vient :

\frac{GM_{T} }{\left(R_{\text{iss}} \right)^{2} } \vec{n}= \vec{a}= \frac{V^{2}}{R_{\text{iss}}}\vec{n}

Autrement dit :

\frac{GM_{T} }{\left(R_{\text{iss}} \right)^{2} } = \frac{V^{2}}{R_{\text{iss}}}

V^{2} =\frac{GM_{T} R_{\text{iss}} }{\left(R_{\text{iss}} \right)^{2} }

V^{2} =\frac{GM_{T} }{R_{\text{iss}} }

V=\sqrt{\frac{GM_{T} }{R_{\text{iss}} } }

Question 17

La période de révolution de la Station sur son orbite est :
$T_{\text{iss}} =2\pi \sqrt{\frac{R_{\text{iss}} }{GM{}_{T} } }$
$T_{\text{iss}} =2\pi \sqrt{\frac{\left(R_{\text{iss}} \right)^{3} }{GM{}_{T} } }$
$T_{\text{iss}} =2\pi \sqrt{\frac{GM{}_{T} }{R_{\text{iss}} } }$
$T_{\text{iss}} =2\pi \sqrt{\frac{GM{}_{T} }{\left(R_{\text{iss}} \right)^{3} } }$

Correction

La bonne réponse est b.
La trajectoire de l'ISS est semblable à un cercle de rayon

R_{\text{iss}}

.

1

tour est égale à

2\pi R_{\text{iss}}

.
L'iSS effectue ce tour à la vitesse

V

, et elle met donc un temps

T

(

1

période) pour effectuer ce tour.
On utilise la relation :

\text{TEMPS}=\frac{\text{DISTANCE}}{\text{VITESSE}}

pour trouver

T

.

T=\frac{2\pi R_{\text{iss}} }{V}

T=\frac{2\pi R_{\text{iss}} }{\sqrt{\frac{GM_{T} }{R_{\text{iss}} } } }

T=\frac{2\pi \sqrt{\left(R_{\text{iss}} \right)^{2} } }{\sqrt{\frac{GM_{T} }{R_{\text{iss}} } } }

T=2\pi \sqrt{\frac{\left(R_{\text{iss}} \right)^{2} }{\left(\frac{GM_{T} }{R_{\text{iss}} } \right)} }

\frac{a}{\left(\frac{b}{c} \right)} =a\times \frac{c}{b}

T=2\pi \sqrt{\left(R_{\text{iss}} \right)^{2} \times \frac{R_{\text{iss}} }{GM_{T} } }

T=2\pi \sqrt{\frac{\left(R_{\text{iss}} \right)^{3} }{GM_{T} } }

Question 18

L’énergie mécanique de la Station Spatiale Internationale au cours du temps :
diminue
augmente
reste constante
est nulle

Correction

La bonne réponse est c.
L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle.

E_{m}=E_{c}+E_{p}

.
Or la vitesse de l'ISS est constante donc

E_{c}=\text{constante}

et l'ISS reste à la même altitude donc

E_{p}=\text{constante}

Il en résulte donc que l'énergie mécanique reste constante.
Il y a une deuxième façon de prouver que l'énergie mécanique reste constante.
La variation de

E_{m}

, si

E_{m}

n'est pas constante, est égale au travail des forces non conservatrices que subit l'objet. Or le poids est une force conservatrice, donc l'énergie mécanique reste constante.

Concours Avenir 2018 - Exercice 1

Afin de pouvoir décoller et quitter le sol terrestre, la fusée doit acquérir une accélération de norme : nulle inférieure à gggégale à ggg supérieur à ggg

Au cours du décollage, la quantité de mouvement du système {fusée + gaz} : diminue reste constanteaugmente est nulle

Pour déterminer l’accélération, on utilisera ici : la 111ère loi de Newton la 222ème loi de Newtonla 222ème loi de Keplerla 333ème loi de Kepler

L’accélération de la fusée pendant cette phase a pour expression : a⃗=g⃗\vec{a}=\vec{g}a=g​ a⃗=−g⃗\vec{a}=-\vec{g}a=−g​a⃗=P⃗\vec{a}=\vec{P}a=Pa⃗=−P⃗\vec{a}=-\vec{P}a=−P

Pour obtenir l’expression des coordonnées de la fusée en fonction du temps, il faut : dériver l’accélération dériver la dérivée de l’accélération obtenir la primitive de l’accélération obtenir la primitive de la primitive de l’accélération

Pour étudier la trajectoire de la Station Spatiale Internationale ISS (masse MSM_{S}MS​) autour de la Terre (masse MTM_{T}MT​), il faut se placer dans le référentiel : héliocentrique géocentrique terrestre de Kepler

Une des lois de Kepler permet de relier la période d’un Astre sur son orbite au rayon de celle-ci. Il s’agit : de la 111ère loi de Kepler de la 222ème loi de Kepler de la loi des aires de la 333ème loi de Kepler

En doublant la distance entre la Station Spatiale Internationale et la Terre, la période de révolution de la station sera : multipliée par 222 multipliée par 8\sqrt{8}8​ multipliée par 444 multipliée par 888

L’accélération de la station est : centripète centrifuge tangente à la trajectoire nulle

L’énergie mécanique de la Station Spatiale Internationale au cours du temps : diminue augmente reste constante est nulle

Afin de pouvoir décoller et quitter le sol terrestre, la fusée doit acquérir une accélération de norme :
nulle
inférieure à $g$
égale à $g$
supérieur à $g$

Au cours du décollage, la quantité de mouvement du système {fusée + gaz} :
diminue
reste constante
augmente
est nulle

Pour déterminer l’accélération, on utilisera ici :
la $1$ ^ère loi de Newton
la $2$ ^ème loi de Newton
la $2$ ^ème loi de Kepler
la $3$ ^ème loi de Kepler

L’accélération de la fusée pendant cette phase a pour expression :
$\vec{a}=\vec{g}$
$\vec{a}=-\vec{g}$
$\vec{a}=\vec{P}$
$\vec{a}=-\vec{P}$

Pour obtenir l’expression des coordonnées de la fusée en fonction du temps, il faut :
dériver l’accélération
dériver la dérivée de l’accélération
obtenir la primitive de l’accélération
obtenir la primitive de la primitive de l’accélération

Pour étudier la trajectoire de la Station Spatiale Internationale ISS (masse $M_{S}$ ) autour de la Terre (masse $M_{T}$ ), il faut se placer dans le référentiel :
héliocentrique
géocentrique
terrestre
de Kepler

Une des lois de Kepler permet de relier la période d’un Astre sur son orbite au rayon de celle-ci. Il s’agit :
de la $1$ ^ère loi de Kepler
de la $2$ ^ème loi de Kepler
de la loi des aires
de la $3$ ^ème loi de Kepler

En doublant la distance entre la Station Spatiale Internationale et la Terre, la période de révolution de la station sera :
multipliée par $2$
multipliée par $\sqrt{8}$
multipliée par $4$
multipliée par $8$

L’accélération de la station est :
centripète
centrifuge
tangente à la trajectoire
nulle

L’énergie mécanique de la Station Spatiale Internationale au cours du temps :
diminue
augmente
reste constante
est nulle