Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →

Tchat avec un prof

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →

Concours Avenir 2014 - Exercice 2

1 min

Question 1

La houle est constituée de vagues formées par le vent, qui peuvent se propager sur de grandes distances et donc être observées dans des régions dépourvues de vent. On assimilera la houle à une onde mécanique progressive sinusoïdale. La hauteur de la houle est, par définition, égale au double de l’amplitude mesurée par rapport au niveau de la mer calme.
Deux bouées distantes de

D = 50

m sont alignées dans le sens de propagation de la houle (voir schéma ci-dessous).

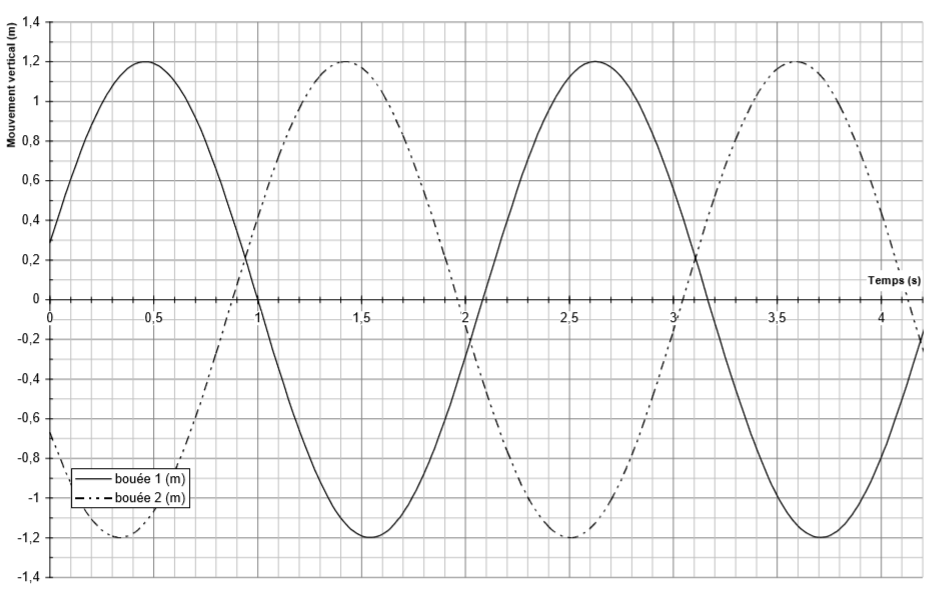
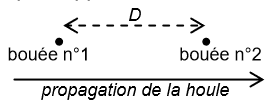Chacune est munie d’un accéléromètre qui enregistre leur déplacement vertical en fonction du temps. Les données recueillies sont présentées dans le graphe ci-dessous :

La hauteur $h$ de la houle est :
$h=1,0$ m
$h=1,2$ m
$h=2,1$ m
$h=2,4$ m

Correction

La bonne réponse est d.
Par lecture directe, de "crête à creux" , la hauteur de la houle mesure

h=2,4

Question 2

La période $T$ de la houle est :
$T = 1,19$ s
$T = 2,17$ s
$T = 3,16$ s
$T = 3,63$ s

Correction

La bonne réponse est b.
Par lecture directe sur l'axe des abscisses ( le temps ), un point de la houle revient dans le même "état vibratoire" avec une période de

T = 2,17

s. Par exemple, au point d'abscisse

1

la sinusoïde qui représente la bouée 1 revient à au même état au point d'abscisse 3,17 ainsi la période est bien de

T = 2,17

Question 3

La fréquence $f$ de la houle est :
$f = 0,32$ Hz
$f = 0,46$ Hz
$f = 0,67$ Hz
$f = 0,84$ Hz

Correction

La bonne réponse est b.
Par définition :

{\text{fréquence}} = \frac{1}{\text{période}}

où la fréquence est en Hertz et la période en seconde.
Donc :

f=\frac{1}{2,17}=0,46

Question 4

Le plus petit retard apparent lu sur le graphique, de la houle entre les deux bouées est :

$\Delta t_{app} =0,20$ s
$\Delta t_{app} =0,96$ s
$\Delta t_{app} =1,09$ s
$\Delta t_{app} =1,22$ s

Correction

La bonne réponse est b.
Par lecture directe, il faut regarder l'écart temporel entre une crête de la bouée

2

et une crête de la bouée

1

. Cela représente le temps de propagation de la houle entre les deux bouées.

Ainsi :

\Delta t_{app} =0,96

Question 5

Le vrai retard de la houle entre les deux bouées vaut : $\Delta t=3\times T+\Delta t_{app} =7,5$ s. L’expression de la célérité de la houle est alors :
$V=D\cdot \Delta t$
$V=\frac{\Delta t}{D}$
$V=D\cdot \frac{\Delta t}{T}$
$V=\frac{D}{\Delta t}$

Correction

La bonne réponse est d.
La relation du cours est :

{\text{vitesse}} = \frac{\text{distance}}{\text{temps}}

soit

V=\frac{D}{\Delta t}

Question 6

La valeur numérique de la célérité est :
$V = 6,7$ m.s $^{-1}$
$V = 11$ m.s $^{-1}$
$V = 15$ m.s $^{-1}$
$V = 21$ m.s $^{-1}$

Correction

La bonne réponse est a.
Nous savons que

V=\frac{D}{\Delta t}

D'après la question

16

, nous savons que :

\Delta t=7,5

s et d'après les hypothèses initiales

D=50

m.
Ainsi :

V=\frac{50}{7,5}

d'où :

V = 6,7

m.s

^{-1}

Question 7

La longueur d’onde de la houle est :
$\lambda =\frac{D}{\Delta t}$
$\lambda =\frac{D\cdot T}{\Delta t}$
$\lambda =\frac{D\cdot \Delta t}{T}$
$\lambda =\frac{T}{D\cdot \Delta t}$

Correction

La bonne réponse est b.
L'expression du cours à connaître est :

{\text{longueur d'onde}}\times{\text{fréquence}}={\text{vitesse ou célérité}}

Autrement dit :

\lambda \times f =V

Or nous savons que la fréquence

f

s'écrit :

f=\frac{1}{T}

et que la vitesse

V

s'écrit :

V=\frac{D}{\Delta t}

Il en résulte donc que :

\lambda \times f =V

équivaut successivement à :

\lambda \times \frac{1}{T} =\frac{D}{\Delta t}

Finalement :

\lambda =\frac{D\cdot T}{\Delta t}

Question 8

Quand la hauteur de la houle augmente, on remarque que la période $T$ des oscillations augmente, ainsi que la distance $L$ entre deux vagues successives. Pour $h = 10$ m, on mesure alors $T = 5$ s et $L = 80$ m. La célérité est :
$V = 8$ m.s $^{-1}$
$V = 16$ m.s $^{-1}$
$V = 40$ m.s $^{-1}$
$V = 62$ m.s $^{-1}$

Correction

La bonne réponse est b.
La houle parcourt

80

mètres en

5

secondes. Sa vitesse est donc

V=\frac{80}{5}=16

m.s

^{-1}

Question 9

Dans un milieu donné dit dispersif la vitesse de propagation d’une onde dépend de sa fréquence. Le milieu de propagation est-il dispersif ?
oui
non
pour le savoir, il faut encore effectuer le calcul d’une autre grandeur
aucun de ces calculs n’est en mesure de le montrer

Correction

La bonne réponse est a.
Le milieu est dispersif car la période, donc la fréquence, fait varier la vitesse de propagation.

Par définition, l'eau est un milieu dispersif .

Question 10

Depuis

2004

, une centrale électrique installée au large de Santona, au nord de l’Espagne, exploite l’énergie de la houle. Elle couvre une surface de

2000

^{2}

mais elle est entièrement immergée et ne perturbe pas le trafic maritime. Elle est constituée de compartiments articulés dont les mouvements, sous l’effet des oscillations des vagues, propulsent de l’eau dans une turbine.
Nous allons vérifier l’ordre de grandeur de la puissance électrique générée. On peut considérer qu’à intervalles périodiques, une masse d’eau se situant au-dessus des

2000

^{2}

de la centrale descend d’une hauteur

h

(la hauteur de la houle). La centrale récupère alors l’énergie potentielle de l’eau.
Dans la suite, on considérera une hauteur

h = 1

m. On prendra pour le champ de pesanteur

g = 10

m.s

^{-2}

La valeur de la masse d’eau, située au-dessus des $2000$ m $^{2}$ , descendant périodiquement d’une hauteur de $1$ m est :
$m=2\times 10^{2}$ kg
$m=2\times 10^{4}$ kg
$m=2\times 10^{6}$ kg
$m=2\times 10^{8}$ kg

Correction

La bonne réponse est c.
Considérons un volume ( parallélépipède ) de volume

2000

^{2}

\times 1

=2000

^{3}

.
Or :

1

^{3}

contient

1\cdot 10^{3}

kg d'eau.
Donc la masse d'eau est :

m=1\cdot 10^{3} \times 2000

m=2\cdot 10^{6}

Question 11

L’énergie potentielle libérée par le mouvement de la cette masse d’eau, considérée comme due à une vague de houle, est (en prenant comme référence $E_{p}=0$ le point le plus bas du mouvement) :
$E_{p} =\frac{1}{2} m\cdot g\cdot h^{2}$
$E_{p} = m\cdot g\cdot h^{2}$
$E_{p} =\frac{1}{2} m\cdot g\cdot h$
$E_{p} =m\cdot g\cdot h$

Correction

La bonne réponse est d.

Par définition, l'expression de l'énergie potentielle est :

E_{p} =m\cdot g\cdot h

Question 12

Dans le cas où la période des vagues est de $10$ secondes, la puissance moyenne récupérable est :
$P = 2$ MW
$P = 20$ MW
$P = 200$ MW
$P = 2$ GW

Correction

La bonne réponse est a.
Toutes les

10

secondes, une énergie potentielle

E_{p} =m\cdot g\cdot h

est récupérée.

E_{p} =m\cdot g\cdot h

Or nous savons que

m=2\cdot 10^{6}

kg d'après la question

21

et d'après les hypothèses nous avons une hauteur

h = 1

m. On prendra pour le champ de pesanteur

g = 10

m.s

^{-2}

D'où :

E_{p} =2\cdot 10^{6} \times10\times1=2\cdot 10^{7}

Joules.
Or la puissance (exprimés en watt ) est le nombres de joules récupérés par seconde, donc :

P=\frac{E_{p}}{10}

équivaut successivement à :

P=\frac{2\cdot 10^{7}}{10}

P=2\cdot 10^{6}

W et donc

P = 2

car

10^{6}

=1

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.

Concours Avenir 2014 - Exercice 2

La hauteur hhh de la houle est : h=1,0h=1,0h=1,0 mh=1,2h=1,2h=1,2 m h=2,1h=2,1h=2,1 m h=2,4h=2,4h=2,4 m

La période TTT de la houle est :T=1,19T = 1,19 T=1,19 sT=2,17T = 2,17 T=2,17 s T=3,16T = 3,16 T=3,16 s T=3,63T = 3,63 T=3,63 s

La fréquence fff de la houle est :f=0,32f = 0,32 f=0,32 Hzf=0,46f = 0,46 f=0,46 Hz f=0,67f = 0,67 f=0,67 Hz f=0,84f = 0,84 f=0,84 Hz

Le plus petit retard apparent lu sur le graphique, de la houle entre les deux bouées est : Δtapp=0,20\Delta t_{app} =0,20Δtapp​=0,20 s Δtapp=0,96\Delta t_{app} =0,96Δtapp​=0,96 s Δtapp=1,09\Delta t_{app} =1,09Δtapp​=1,09 sΔtapp=1,22\Delta t_{app} =1,22Δtapp​=1,22 s

La valeur numérique de la célérité est : V=6,7V = 6,7V=6,7 m.s−1^{-1}−1 V=11V = 11V=11 m.s−1^{-1}−1 V=15V = 15V=15 m.s−1^{-1}−1V=21V = 21V=21 m.s−1^{-1}−1

La longueur d’onde de la houle est : λ=DΔt\lambda =\frac{D}{\Delta t}λ=ΔtD​λ=D⋅TΔt\lambda =\frac{D\cdot T}{\Delta t}λ=ΔtD⋅T​λ=D⋅ΔtT\lambda =\frac{D\cdot \Delta t}{T}λ=TD⋅Δt​λ=TD⋅Δt\lambda =\frac{T}{D\cdot \Delta t}λ=D⋅ΔtT​

Dans un milieu donné dit dispersif la vitesse de propagation d’une onde dépend de sa fréquence. Le milieu de propagation est-il dispersif ?oui non pour le savoir, il faut encore effectuer le calcul d’une autre grandeur aucun de ces calculs n’est en mesure de le montrer

La valeur de la masse d’eau, située au-dessus des 200020002000 m2^{2}2, descendant périodiquement d’une hauteur de 111 m est :m=2×102m=2\times 10^{2}m=2×102 kgm=2×104m=2\times 10^{4}m=2×104 kg m=2×106m=2\times 10^{6}m=2×106 kg m=2×108m=2\times 10^{8}m=2×108 kg

Dans le cas où la période des vagues est de 101010 secondes, la puissance moyenne récupérable est : P=2P = 2P=2 MW P=20P = 20P=20 MW P=200P = 200P=200 MW P=2P = 2P=2 GW

La hauteur $h$ de la houle est :
$h=1,0$ m
$h=1,2$ m
$h=2,1$ m
$h=2,4$ m

La période $T$ de la houle est :
$T = 1,19$ s
$T = 2,17$ s
$T = 3,16$ s
$T = 3,63$ s

La fréquence $f$ de la houle est :
$f = 0,32$ Hz
$f = 0,46$ Hz
$f = 0,67$ Hz
$f = 0,84$ Hz

Le plus petit retard apparent lu sur le graphique, de la houle entre les deux bouées est :

$\Delta t_{app} =0,20$ s
$\Delta t_{app} =0,96$ s
$\Delta t_{app} =1,09$ s
$\Delta t_{app} =1,22$ s

La valeur numérique de la célérité est :
$V = 6,7$ m.s $^{-1}$
$V = 11$ m.s $^{-1}$
$V = 15$ m.s $^{-1}$
$V = 21$ m.s $^{-1}$

La longueur d’onde de la houle est :
$\lambda =\frac{D}{\Delta t}$
$\lambda =\frac{D\cdot T}{\Delta t}$
$\lambda =\frac{D\cdot \Delta t}{T}$
$\lambda =\frac{T}{D\cdot \Delta t}$

Dans un milieu donné dit dispersif la vitesse de propagation d’une onde dépend de sa fréquence. Le milieu de propagation est-il dispersif ?
oui
non
pour le savoir, il faut encore effectuer le calcul d’une autre grandeur
aucun de ces calculs n’est en mesure de le montrer

La valeur de la masse d’eau, située au-dessus des $2000$ m $^{2}$ , descendant périodiquement d’une hauteur de $1$ m est :
$m=2\times 10^{2}$ kg
$m=2\times 10^{4}$ kg
$m=2\times 10^{6}$ kg
$m=2\times 10^{8}$ kg

Dans le cas où la période des vagues est de $10$ secondes, la puissance moyenne récupérable est :
$P = 2$ MW
$P = 20$ MW
$P = 200$ MW
$P = 2$ GW