Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Tchat avec un prof

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Concours Avenir 2014 - Exercice 1

1 min
0
Question 1
Un smartphone du marché, équipé d’un appareil photo, possède un objectif composé d’une lentille de diamètre a=1a = 1 mm. À l’intérieur du boîtier de l’appareil, un capteur de 88 mégapixels et de surface 1616 mm2^{2} est situé à une distance D=2,8D = 2,8 mm de l’objectif.
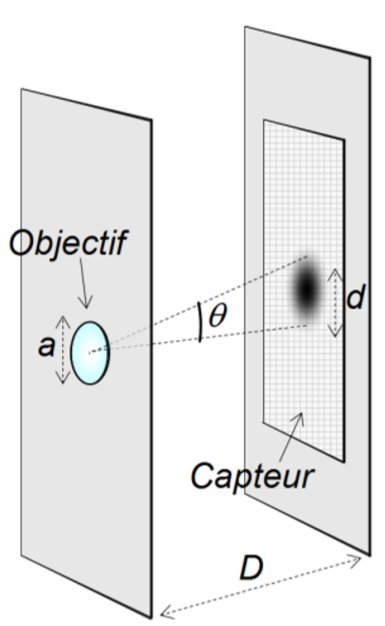
La diffraction, due à la taille de la lentille, limite la résolution de l’appareil photo. L’exercice permettra de comparer la taille de la tache principale de diffraction et la taille d’un pixel.

Avec λ\lambda la longueur d’onde de la lumière incidente, l’ouverture angulaire θ\theta de la tache centrale de diffraction (la tache d'Airy) est :
  • θ=λD\theta =\frac{\lambda }{D}
  • θ=λa\theta =\frac{\lambda }{a}
  • θ=Dλ\theta =\frac{D}{\lambda }
  • θ=aλ\theta =\frac{a}{\lambda }

Correction
La bonne réponse est b.
Dans le cas de la diffraction d'une onde lumineuse, de longueur d'onde λ\lambda , par une fente de largeur aa (ou un fil de diamètre aa ), l'écart angulaire de diffraction θ\theta a pour expression :
θ=λa\theta =\frac{\lambda }{a}

Avec :
  • λ\lambda en mètre (m)\left(m\right)
  • aa en mètre (m)\left(m\right)
  • θ\theta en radian (rad)\left(rad\right)
    • Question 2

    Pour cet appareil photo, la diffraction est un peu moins prononcée dans le cas d’une lumière :
    • violette
    • verte
    • jaune
    • rouge

    Correction
    La bonne réponse est a.
    Les différentes longueurs d'onde des 44 couleurs proposées sont dans l'ordre croissant :
    λVIOLET<λVERT<λJAUNE<λROUGE\lambda _{\text{VIOLET}}<\lambda _{\text{VERT}}<\lambda _{\text{JAUNE}}<\lambda _{\text{ROUGE}}
    La diffraction θ=λa\theta =\frac{\lambda }{a} est moins prononcé pour un λ\lambda "petit", donc pour le violet.
    Question 3

    La longueur d’onde moyenne du spectre visible est de l’ordre de :
    • λ=5×10−6\lambda =5\times 10^{-6} m
    • λ=5×10−7\lambda =5\times 10^{-7} m
    • λ=5×10−8\lambda =5\times 10^{-8} m
    • λ=5×10−9\lambda =5\times 10^{-9} m

    Correction
    La bonne réponse est b.
    Le spectre visible s'étale de λVIOLET=350\lambda _{\text{VIOLET}}=350 nmnm à λROUGE=800\lambda _{\text{ROUGE}}=800 nmnm.
    Or 11 nmnm =1⋅10−9=1\cdot 10^{-9} mm
    Ainsi, le spectre visible s'étale de λVIOLET=3,5×10−7\lambda _{\text{VIOLET}}=3,5\times 10^{-7} mm à λROUGE=8×10−7\lambda _{\text{ROUGE}}=8\times 10^{-7} mm
    La réponse doit donc s'exprimer à l'aide de 10−710^{-7} mm et seule la réponse bb propose un tel résultat.
    Question 4

    L'angle θ\theta étant petit, on fait l’approximation que tan⁡(θ)≈θ\tan \left(\theta \right)\approx \theta. Le diamètre dd de la tache centrale de diffraction correspondante, au niveau du capteur, est :
    • d=λ⋅aDd=\frac{\lambda \cdot a}{D}
    • d=D⋅aλd=\frac{D\cdot a}{\lambda }
    • d=λ⋅Dad=\frac{\lambda \cdot D}{a}
    • d=aλ⋅Dd=\frac{a}{\lambda \cdot D}

    Correction
    La bonne réponse est c.
    On sait que θ=λa\theta =\frac{\lambda }{a} et que pour un angle θ\theta , la tangente de cet angle se calcule en faisant le rapport du coté opposé sur le coté adjacent.
    D'après le graphique, donné ci-dessous :
    Le coté opposé est égale à dd et le coté adjacent est égale à DD. Il en résulte donc que :
  • tan⁡(θ)=dD\tan \left(\theta \right)=\frac{d}{D}
  • tan⁡(θ)≈θ\tan \left(\theta \right)\approx \theta
  • θ=λa\theta =\frac{\lambda }{a}
    • Ainsi : dD=λa\frac{d}{D} =\frac{\lambda }{a} et finalement :
    d=λ⋅Dad=\frac{\lambda \cdot D}{a}
    Question 5

    Application numérique. Le diamètre moyen dd de la tache est :
    • d=1,8d = 1,8 nm
    • d=1,4d = 1,4 μ \mum
    • d=1,8d = 1,8 μ\mum
    • d=5,6d = 5,6 μ\mum

    Correction
    La bonne réponse est b.
    D'après l'énoncé, on sait que :
    a=1a = 1 mm donc a=1⋅10−3a = 1\cdot 10^{-3} m
    D=2,8D = 2,8 mm donc a=2,8⋅10−3a = 2,8\cdot 10^{-3} m
    λ=5×10−7\lambda =5\times 10^{-7} m ( d'après la question 33 )
    Or :
    d=λ⋅Dad=\frac{\lambda \cdot D}{a} équivaut successivement à :
    d=5⋅10−7×2,8⋅10−31⋅10−3d=\frac{5\cdot 10^{-7} \times 2,8\cdot 10^{-3} }{1\cdot 10^{-3} }
    d=5×2,8×10−3×10−71⋅10−3d=\frac{5\times 2,8\times 10^{-3} \times 10^{-7} }{1\cdot 10^{-3} }
    d=14×10−7d=14\times 10^{-7}
    d=1,4×10−6d=1,4\times 10^{-6} m
    d=1,4d=1,4 μ\mum
    Question 6

    La surface SS d’un pixel est :
    • S=2×10−12S=2\times 10^{-12} m2^{2}
    • S=2×10−9S=2\times 10^{-9} m2^{2}
    • S=2×10−6S=2\times 10^{-6} m2^{2}
    • S=2×10−3S=2\times 10^{-3} m2^{2}

    Correction
    La bonne réponse est a.
    Il y a 88 mégapixels ( 88 millions ) sur une surface de 1616 mm2^{2}.
    Or 11 mm2^{2} vaut 1⋅10−61\cdot 10^{-6} m2^{2}.
    Ainsi :
    S=16⋅10−68⋅106S=\frac{16\cdot 10^{-6} }{8\cdot 10^{6} }
    S=2×10−12S=2\times 10^{-12} m2^{2}
    Question 7
    À la sortie du capteur, la photo est codée en une suite de nombres. Dans l’encodage « RGB 2424 bits » le plus standard (ou RVB), chaque pixel est représenté par 33 nombres de 00 à 255255, représentant les intensités lumineuses respectivement de la composante rouge, verte et bleue, de la lumière captée.

    Dans ce type de codage, un pixel représenté par les nombres (255,255,0)\left(255,255,0\right) correspond à une lumière :
    • jaune
    • cyan
    • magenta
    • grise

    Correction
    La bonne réponse est a.
    En RVB, le codage (255,255,0)\left(255,255,0\right) représente le mélange des couleurs rouge + vert, donc à la couleur jaune.
    Question 8

    En l’absence de compression numérique, la taille (en mégaoctets) du fichier (Bitmap) contenant la photo, est :
    • 44 Mo
    • 88 Mo
    • 1616 Mo
    • 2424 Mo

    Correction
    La bonne réponse est d.
    En codage RVB, un pixel est codé par 33 octets, il y a 88 millions de pixel, donc la taille du fichier en absence de compression est :
    3×8×106=243\times 8\times 10^{6} =24 Mo
    Question 9
    On règle le taux de compression de manière à obtenir un fichier JPEG de 44 Mo.
    On envoie ce fichier par mail depuis le téléphone mobile, au moyen d’une connexion à un réseau hertzien de quatrième génération (LTE ou « 4G4G ») dont le débit est d’environ 4040 Mbps (mégabits par seconde).

    La durée théorique du transfert des données (hors durée d’accès au serveur) est :
    • 0,10,1 s
    • 0,80,8 s
    • 55 s
    • 2020 s

    Correction
    La bonne réponse est b.
    11 octet représente 88 bits, un fichier de 44 Mo en contient donc 4⋅106×8=3,2⋅1074\cdot 10^{6}\times8=3,2\cdot 10^{7} bits.
    Avec un débit de 4040 Mbps (mégabits par seconde) où 4040 Mbps est égale à 40⋅10640\cdot 10^{6} bits, on trouve un temps de transfert de :
    t=3,2⋅10740⋅106t=\frac{3,2\cdot 10^{7} }{40\cdot 10^{6} }
    t=0,8t =0,8 s

    Question 10
    On rappelle que log⁡(10n)=n\log \left(10^{n} \right)=n.

    Le signal reçu est la somme {signal à transmettre + bruit}.
    Pour pouvoir le décoder correctement, il faut que le rapport en dB signal / bruit soit au moins de 2020 dB. Le rapport entre la puissance du signal reçu et la puissance moyenne des parasites (le bruit) doit être au moins :
    • 22
    • 1010
    • 2020
    • 100100

    Correction
    La bonne réponse est d.
    L'expression du cours à connaitre est :
    L'atténuation du signal AA d'une transmission est : A=10log⁡(PentreˊePsortie)A=10\log \left(\frac{P_{\text{entrée}} }{P_{sortie} } \right)
    Soit ici :
    10log⁡(Psignal recuPbruit)=2010\log \left(\frac{P_{\text{signal recu}} }{P_{bruit} } \right)=20
    log⁡(Psignal recuPbruit)=2\log \left(\frac{P_{\text{signal recu}} }{P_{bruit} } \right)=2 . Or , on nous indique que log⁡(10n)=n\log \left(10^{n} \right)=n ce qui veut dire que log⁡(102)=2\log \left(10^{2} \right)=2
    D'où :
    log⁡(Psignal recuPbruit)=log⁡(102)\log \left(\frac{P_{\text{signal recu}} }{P_{bruit} } \right)=\log \left(10^{2} \right).
    Or : log⁡(A)=log⁡(B)⇔A=B\log \left(A\right)=\log \left(B\right)\Leftrightarrow A=B
    Il en résulte donc que :
    Psignal recuPbruit=102=100\frac{P_{\text{signal recu}} }{P_{bruit} }=10^{2}=100

    Question 11

    Le signal reçu est amplifié 1010 fois. Le nouveau rapport en dB signal / bruit est de :
    • 2020 dB
    • 2323 dB
    • 3030 dB
    • 200200 dB

    Correction
    La bonne réponse est a.
    Le signal reçu est la somme {signal à transmettre + bruit}. Or si l'ensemble de ce signal est amplifié 1010 fois, le bruit est aussi amplifié 1010 fois. Le rapport ne change pas . Ainsi le rapport en dB signal / bruit est toujours de 2020 dB.

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.