Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Savoir calculer l'aire d'une figure - Exercice 1

8 min
15
Question 1

Définition de l'aire d'une figure.

Correction
L’aire d’une figure correspond à la mesure de sa surface intérieure.
La figure ci-dessous occupe une surface (qui a été hachurée), dont on peut calculer l’aire.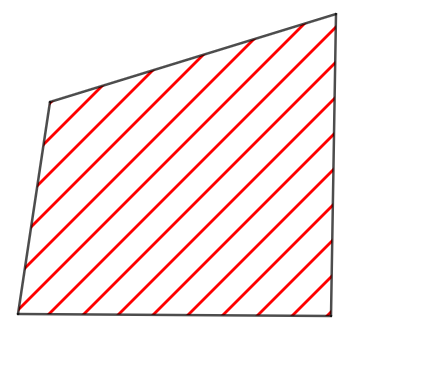
Important : L’unité de référence pour l'aire d'une figure est le mètre-carré (m2)(m^2).
Les divisions du mètre carré sont :
  • Le décimètre-carré (1  dm2).\color{blue}(1\;dm^2).
  • Le centimètre-carré (1  cm2).\color{blue}(1\;cm^2).
  • Le millimètre-carré (1  mm2).\color{blue}(1\;mm^2).
    Les multiples du mètre carré sont :
  • Le décamètre-carré (1  dam2).\color{blue}(1\;dam^2).
  • L'hectomètre-carré (1  hm2).\color{blue}(1\;hm^2).
  • Le kilomètre-carré (1  km2).\color{blue}(1\;km^2).

    • Question 2
    On considère le carré IJKLIJKL ci-dessous :

    Calculer l'aire du carré IJKLIJKL ci-dessus.

    Correction
    L’aire d’une figure correspond à la mesure de sa surface intérieure.

        \;\;L'aire du carré == c×c=c2    c\times{c}=c^2\;\;      \;\;\;⟹      \color{red}\Longrightarrow\;\;\; ou cc représente la longueur d'un côté du carré.


    L'aire du carré IJKLIJKL correspond à sa surface, ici représenté en rouge.
    L'aire du carré IJKLIJKL correspond à :
    Aire du carré IJKL=IJKL= côté ×\times côté       ⟹\;\;\;\color{red}\Longrightarrow Avec côté =IJ=5  m.=IJ=5\;m.
    Aire du carré IJKL=5×5IJKL=5\times5
    Aire  du  carreˊ  IJKL=25  m2\color{blue}\boxed{\bf{Aire \;du\;carré\;IJKL = 25\;m^2}}       \;\;\;On n'oublie pas ici de préciser l'unité d'aire.

    Question 3
    On considère le rectangle ABCDABCD ci-dessous :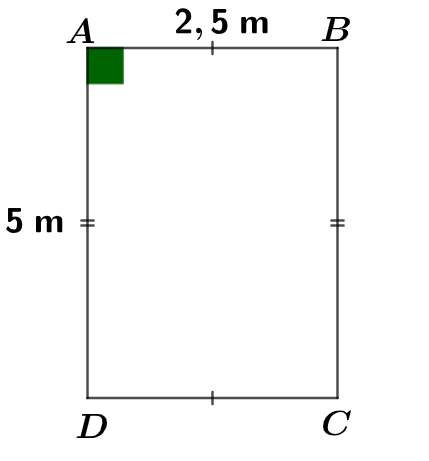

    Calculer l'aire du rectangle ABCDABCD ci-dessus.

    Correction
    L’aire d’une figure correspond à la mesure de sa surface intérieure.

        \;\;L'aire du rectangle ==L×l     {\color{green}L}\times{\color{blue}l}\;\;      \;\;\;⟹      \color{red}\Longrightarrow\;\;\; ou L{\color{green}L} représente la longueur et l{\color{blue}l} représente la largeur.

    L'aire du rectangle ABCDABCD correspond à sa surface, ici représenté en rouge.
    L'aire du rectangle ABCDABCD correspond à :
    Aire du rectangle ABCD=Longueur×largeurABCD={\color{green}Longueur}\times{\color{blue}largeur}       ⟹\;\;\;\color{red}\Longrightarrow ou L=AB=2,5  m\color{green}L=AB=2,5\;m et l=AD=5  m\color{blue}l=AD=5\;m.
    Aire du rectangle ABCD=2,5×5ABCD=2,5\times5
    Aire  du  rectangle  ABCD=12,5  m2\color{blue}\boxed{\bf{Aire \;du\;rectangle\;ABCD = 12,5\;m^2}}       \;\;\;On n'oublie pas ici de préciser l'unité d'aire.

    Question 4
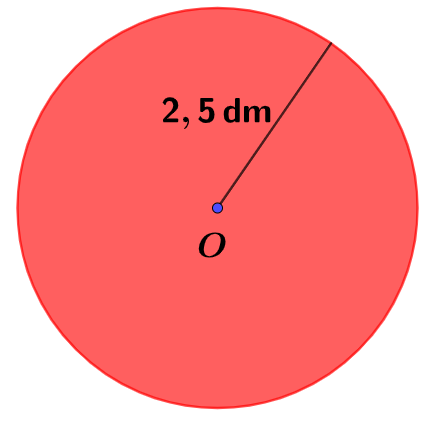
    On considère le cercle de centre OO ci-dessous :

    Calculer l'aire du cercle ci-dessus. Pour cette question, on considère que π=3,14\pi=3,14.

    Correction
    L’aire d’une figure correspond à la mesure de sa surface intérieure.

        \;\;L'aire du cercle ==π×r×r=π×r2     \pi\times{r}\times{r}=\pi\times{{\color{blue}r}^2}\;\;      \;\;\;⟹      \color{red}\Longrightarrow\;\;\; ou r{\color{blue}r} représente le rayon du cercle.

    L'aire du cercle correspond à sa surface, ici représenté en rouge.
    Aire du cercle =π×r2=\pi\times{r^2}       ⟹\;\;\;\color{red}\Longrightarrow ou r=2,5  dm.r=2,5\;dm.
    Aire du cercle =3,14×2,52=3,14\times2,5^2
    Aire  du  cercle=19,625  dm2\color{blue}\boxed{\bf{Aire \;du\;cercle = 19,625\;dm^2}}       \;\;\;On n'oublie pas ici de préciser l'unité d'aire.

    Question 5
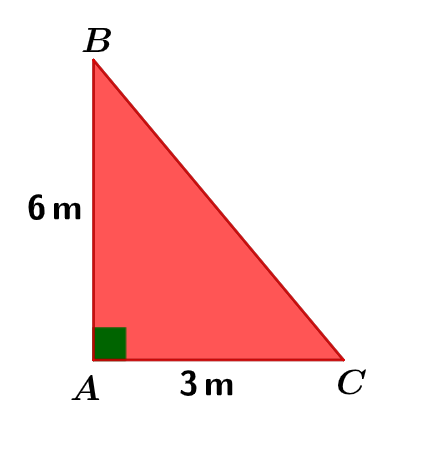
    On considère le triangle ABCABC rectangle en AA ci-dessous :

    Calculer l'aire du triangle rectangle ABCABC ci-dessus.

    Correction
    L’aire d’une figure correspond à la mesure de sa surface intérieure.
    L′aire  du  triangle=base×hauteur2\color{red}\boxed{\bf{L'aire\;du\;triangle = \frac{base\times{hauteur}}{2}}}
    L'aire du triangle ABCABC correspond à sa surface, ici représenté en rouge.
    L'aire du triangle ABCABC correspond à :
    Aire du triangle ABC=base×hauteur2ABC=\frac{{\color{green}base}\times{\color{blue}hauteur}}{2}       ⟹\;\;\;\color{red}\Longrightarrow ou la  base  AC=3  m\color{green}la\;base\;AC=3\;m et la  hauteur=AB=6  m\color{blue}la\;hauteur=AB=6\;m.
    (On aurait pu également dans le cas du triangle rectangle, dire que la base est ABAB et la hauteur ACAC).
    Aire du triangle ABC=3×62ABC=\frac{3\times6}{2}
    Aire  du  triangle  ABC=9  m2\color{blue}\boxed{\bf{Aire \;du\;triangle\;ABC = 9\;m^2}}       \;\;\;On n'oublie pas ici de préciser l'unité d'aire.

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.