Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Reconnaître un parallélogramme - Exercice 3

8 min
20
On considère un triangle IJKIJK tel que :
IJ=5  cm  ;JK=6  cmIJ=5\;cm\;;JK=6\;cm et IK=9  cm.IK=9\;cm.
Question 1

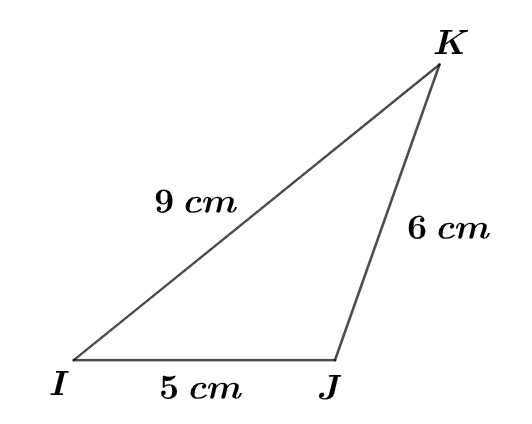
Construire le triangle IJK.IJK.

Correction
Question 2

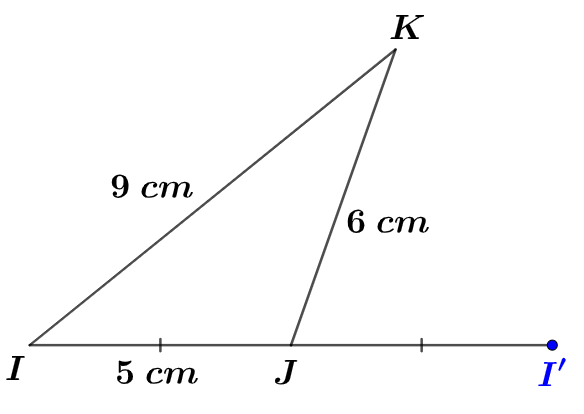
Construire le symétrique de II par rapport au point J.J.

Correction
Question 3

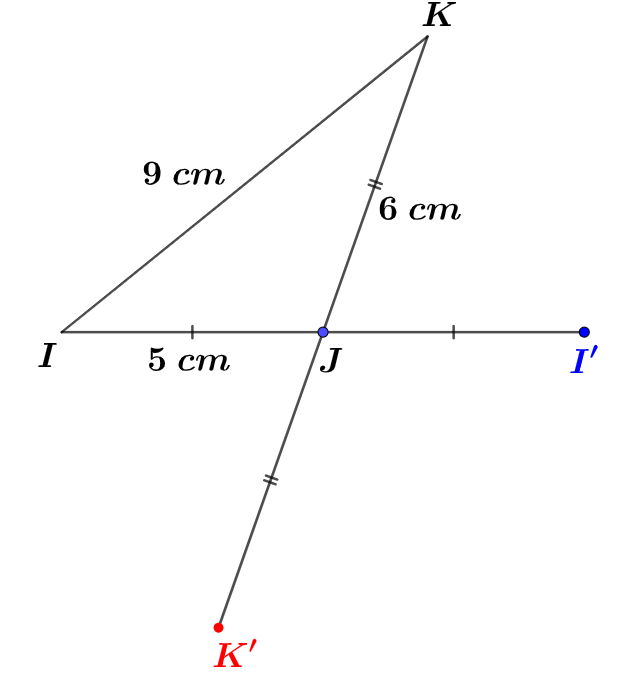
Construire le symétrique de KK par rapport au point J.J.

Correction
Question 4

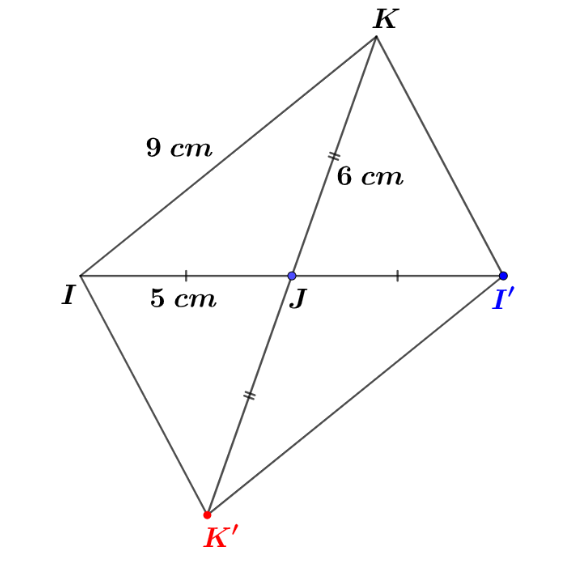
Démontrer que le quadrilatère IKI′K′IKI'K' est un parallélogramme.

Correction
Des questions précédentes, on sait que :
  • I′I' est le symétrique de II par rapport au point JJ.
  • K′K' est le symétrique de KK par rapport au point JJ.
      La symétrie centrale conserve les longueurs des segments.
    On a donc : IJ=JI′IJ=JI' et KJ=JK′KJ=JK'.
    On en déduit donc que le point JJ est le milieu des diagonales KK′KK' et II′II' du quadrilatère IKI′K′IKI'K'.
    Le quadrilatère IKI′K′IKI'K' a ses diagonales qui se coupent en leur milieu .

    • Si un quadrilatère a ses diagonales qui se coupent en leur milieu, alors ce quadrilatère est un parallélogramme.
    On peut donc conclure que le quadrilatère IKI′K′IKI'K' est un parallélogramme.

    • Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.