Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →

Reconnaître un parallélogramme - Exercice 2

8 min

En utilisant le codage des figures ci-dessous, justifier à l'aide d'une propriété de cours que le quadrilatère

ABCD

est un parallélogramme.

Question 1

Correction

Voici les propriétés qui permettent de démontrer qu'un quadrilatère est un parallélogramme :

Un quadrilatère qui a ses diagonales qui se coupent en leur milieu est un parallélogramme.
Un quadrilatère qui a ses côtés opposés $\color{red}2$ à $\color{red}2$ de mêmes longueurs est un parallélogramme.
Un quadrilatère qui a ses côtés opposés parallèles $\color{red}2$ à $\color{red}2$ est un parallélogramme.
Un quadrilatère qui a ses angles opposés de mêmes mesures est un parallélogramme.

Dans le quadrilatère

ABCD

, on a

(AB)

parallèle à

(DC)

(AD)

parallèle à

(BC).

Le quadrilatère $ABCD$ a ses côtés opposés parallèles $\color{red}2$ à $\color{red}2$ .

On peut donc conclure que le quadrilatère $ABCD$ est un parallélogramme.

Question 2

Correction

Voici les propriétés qui permettent de démontrer qu'un quadrilatère est un parallélogramme :

Un quadrilatère qui a ses diagonales qui se coupent en leur milieu est un parallélogramme.
Un quadrilatère qui a ses côtés opposés $\color{red}2$ à $\color{red}2$ de mêmes longueurs est un parallélogramme.
Un quadrilatère qui a ses côtés opposés parallèles $\color{red}2$ à $\color{red}2$ est un parallélogramme.
Un quadrilatère qui a ses angles opposés de mêmes mesures est un parallélogramme.

Dans le quadrilatère

ABCD

, le point

O

est le milieu des deux diagonales

AC

DB.

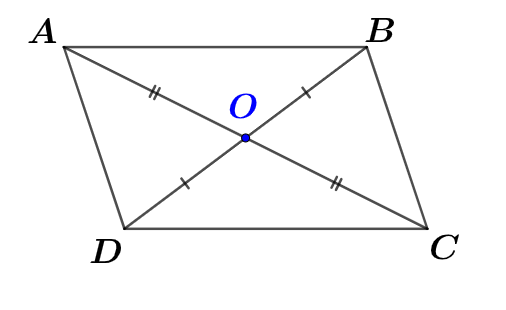
Le quadrilatère $ABCD$ a ses diagonales qui se coupent en leur milieu .

On peut donc conclure que le quadrilatère $ABCD$ est un parallélogramme.

Question 3

Correction

Voici les propriétés qui permettent de démontrer qu'un quadrilatère est un parallélogramme :

Un quadrilatère qui a ses diagonales qui se coupent en leur milieu est un parallélogramme.
Un quadrilatère qui a ses côtés opposés $\color{red}2$ à $\color{red}2$ de mêmes longueurs est un parallélogramme.
Un quadrilatère qui a ses côtés opposés parallèles $\color{red}2$ à $\color{red}2$ est un parallélogramme.
Un quadrilatère qui a ses angles opposés de mêmes mesures est un parallélogramme.

Dans le quadrilatère

ABCD

, on a :

AB=DC

AD=BC

. (Les côtés opposés sont de la même longueur).
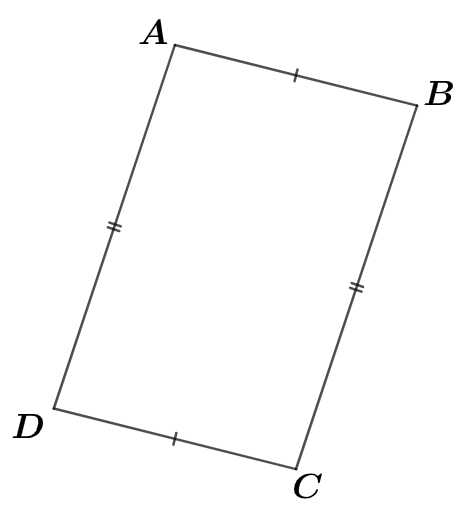
Le quadrilatère $ABCD$ a ses côtés opposés $\color{red}2$ à $\color{red}2$ de mêmes longueurs .

On peut donc conclure que le quadrilatère $ABCD$ est un parallélogramme.

Question 4

Correction

Voici les propriétés qui permettent de démontrer qu'un quadrilatère est un parallélogramme :

Un quadrilatère qui a ses diagonales qui se coupent en leur milieu est un parallélogramme.
Un quadrilatère qui a ses côtés opposés $\color{red}2$ à $\color{red}2$ de mêmes longueurs est un parallélogramme.
Un quadrilatère qui a ses côtés opposés parallèles $\color{red}2$ à $\color{red}2$ est un parallélogramme.
Un quadrilatère qui a ses angles opposés de mêmes mesures est un parallélogramme.

Dans le quadrilatère

ABCD

, on a :

\widehat{ADC}=\widehat{ABC}

\widehat{DAB}=\widehat{DCB}

. (Les angles opposés sont de la même mesure.)
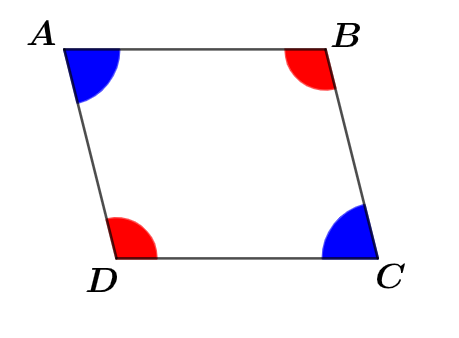
Le quadrilatère $ABCD$ a ses angles opposés de mêmes mesures .

On peut donc conclure que le quadrilatère $ABCD$ est un parallélogramme.

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.