Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ère partie - Exercice 1
5 min
10
Exercices, définitions de cours.
Question 1
Si les points et sont symétriques par rapport au point , que peut-on dire du point
Correction
- Définition d'une symétrie d'un point par une symétrie centrale :
- Le point est le milieu du segment .
Si le point est le symétrique du point par rapport au point O alors :

Question 2
On considère points alignés et
Les points et sont les images respectives des points et par une symétrie de centre .
Les points et sont les images respectives des points et par une symétrie de centre .
Que peut-on dire des points et
Correction
On peut dans un premier temps représenter la situation ci-dessous à l'aide d'une figure :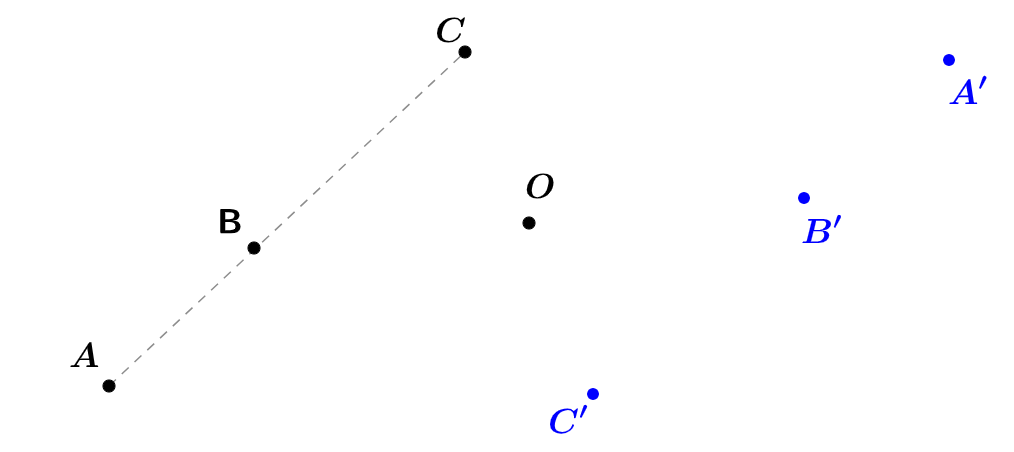 Les points et sont les images respectives des points et par une symétrie de centre .
Les points et sont les images respectives des points et par une symétrie de centre .
Les points et sont alignés.
Or la symétrie centrale conserve l'alignement des points, donc les points et sont alignés.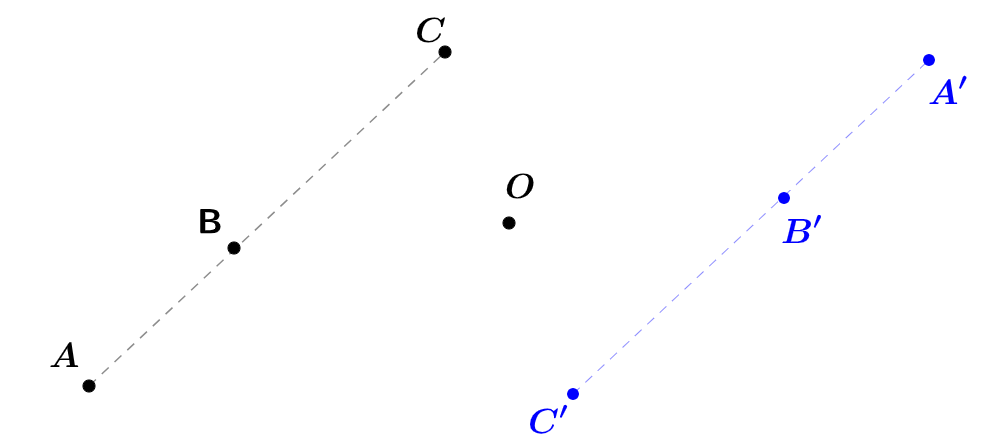

- On sait que la symétrie centrale conserve l’alignement des points.
Les points et sont alignés.
Or la symétrie centrale conserve l'alignement des points, donc les points et sont alignés.

Question 3
Que peut-on dire de deux angles symétriques par rapport à un point
Correction
On peut dans un premier temps représenter la situation ci-dessous à l'aide d'une figure :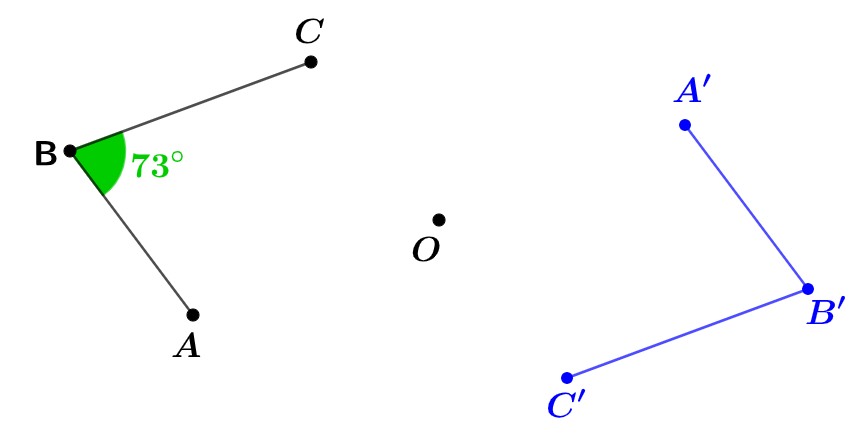 L'image de l'angle est l'angle .
L'image de l'angle est l'angle .
On sait que la symétrie conserve la mesure des angles.
Donc
Cela signifie que deux angles symétriques par rapport à un point seront de la même mesure.

- La symétrie centrale conserve : la mesure des angles.
On sait que la symétrie conserve la mesure des angles.
Donc
Cela signifie que deux angles symétriques par rapport à un point seront de la même mesure.
Question 4
Considérons deux figures symétriques par rapport à un point .
Par quel mouvement passe-t-on de la figure de départ à la figure d'arrivée ?
Par quel mouvement passe-t-on de la figure de départ à la figure d'arrivée ?
Correction
- Deux figures sont symétriques par rapport à un point lorsqu’elles se superposent en effectuant un demi-tour autour de ce point.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.