Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ème partie - Exercice 3
8 min
25
On considère le programme de calcul ci-dessous :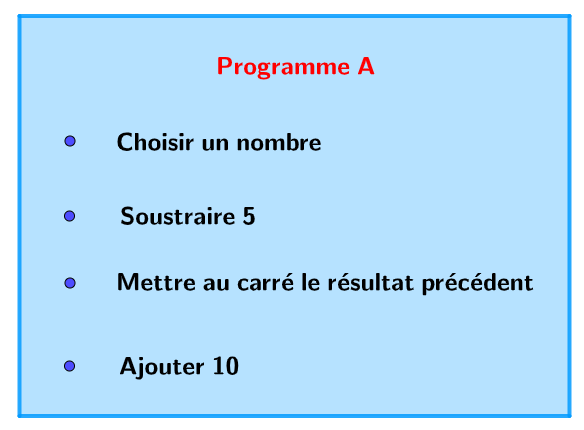

Question 1
Effectuer ce programme de calcul en prenant comme nombre de départ.
Correction
1°) Déterminons le résultat obtenu pour le programme A : (Avec comme nombre de départ 8.)
première étape :
Le nombre choisi est
deuxième étape :
On soustrait à ce nombre. C'est-à-dire soustraire à .
On obtient donc
troisième étape :
On doit mettre au carré le résultat précédent, c'est-à-dire :
Pour rappel : le carré d’un nombre est le résultat de la multiplication de ce nombre par lui-même.
quatrième étape :
On ajoute à ce nombre. C'est-à-dire additionner à .
On peut donc conclure qu'en choisissant comme nombre de départ le résultat final est .
première étape :
Le nombre choisi est
deuxième étape :
On soustrait à ce nombre. C'est-à-dire soustraire à .
On obtient donc
troisième étape :
On doit mettre au carré le résultat précédent, c'est-à-dire :
Pour rappel : le carré d’un nombre est le résultat de la multiplication de ce nombre par lui-même.
quatrième étape :
On ajoute à ce nombre. C'est-à-dire additionner à .
On peut donc conclure qu'en choisissant comme nombre de départ le résultat final est .
Question 2
Effectuer ce programme de calcul en prenant comme nombre de départ.
Correction
1°) Déterminons le résultat obtenu pour le programme A : (Avec comme nombre de départ 10.)
première étape :
Le nombre choisi est
deuxième étape :
On soustrait à ce nombre. C'est-à-dire soustraire à .
On obtient donc
troisième étape :
On doit mettre au carré le résultat précédent, c'est-à-dire :
Pour rappel : le carré d’un nombre est le résultat de la multiplication de ce nombre par lui-même.
quatrième étape :
On ajoute à ce nombre. C'est-à-dire additionner à .
On peut donc conclure qu'en choisissant comme nombre de départ le résultat final est .
première étape :
Le nombre choisi est
deuxième étape :
On soustrait à ce nombre. C'est-à-dire soustraire à .
On obtient donc
troisième étape :
On doit mettre au carré le résultat précédent, c'est-à-dire :
Pour rappel : le carré d’un nombre est le résultat de la multiplication de ce nombre par lui-même.
quatrième étape :
On ajoute à ce nombre. C'est-à-dire additionner à .
On peut donc conclure qu'en choisissant comme nombre de départ le résultat final est .
Question 3
Effectuer ce programme de calcul en prenant comme nombre de départ.
Correction
1°) Déterminons le résultat obtenu pour le programme A : (Avec comme nombre de départ .)
première étape :
Le nombre choisi est
deuxième étape :
On soustrait à ce nombre. C'est-à-dire soustraire à .
On obtient donc
troisième étape :
On doit mettre au carré le résultat précédent, c'est-à-dire :
Ici, il faut bien faire attention de mettre entre parenthèses.
En effet :
quatrième étape :
On ajoute à ce nombre. C'est-à-dire additionner à .
On peut donc conclure qu'en choisissant comme nombre de départ le résultat final est .
première étape :
Le nombre choisi est
deuxième étape :
On soustrait à ce nombre. C'est-à-dire soustraire à .
On obtient donc
troisième étape :
On doit mettre au carré le résultat précédent, c'est-à-dire :
Ici, il faut bien faire attention de mettre entre parenthèses.
En effet :
quatrième étape :
On ajoute à ce nombre. C'est-à-dire additionner à .
On peut donc conclure qu'en choisissant comme nombre de départ le résultat final est .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.