Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Tchat avec un prof

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Construction d'un point par translation (Sur quadrillage) - Exercice 1

8 min
15
Question 1

Exemple : construire à l'aide de la figure ci-dessous l'image du point CC, ( qu'on appellera le point DD) par la translation qui transforme 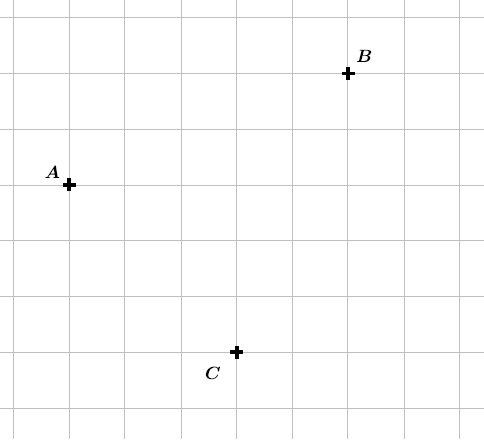AA en BB.

Correction
    Définition d'une translation :

  • Une translation est une transformation géométrique qui permet d'obtenir par glissement d'une figure initiale une figure finale.
  • Ce déplacement, (glissement) doit s'effectuer sans que la figure initiale soit tournée ou déformée.
  • Ce glissement est défini par 3 éléments : un sens, une direction et une longueur.
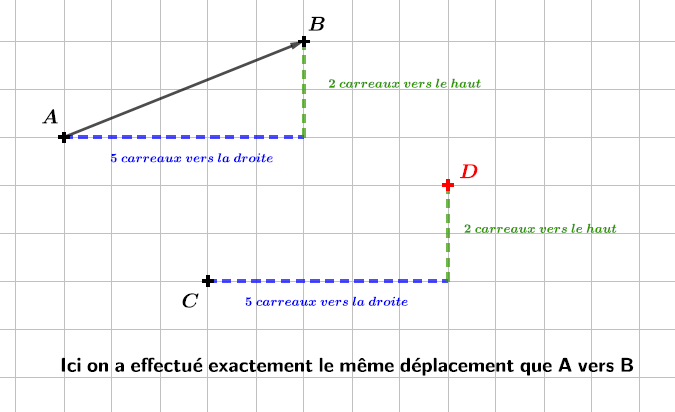
Méthode pour tracer l'image d'un point par une translation à l'aide d'un quadrillage.
1°)1°) Il faut tracer le segment [AB][AB].
2°)2°) Partant du point AA, on se déplace horizontalement pour arriver au niveau du point B.B.
(On part du point AA car on demande la translation qui transforme AA en BB).
3°)3°) Puis on se déplace verticalement pour rejoindre le point BB.
On peut également se déplacer verticalement puis horizontalement, cela ne change rien.
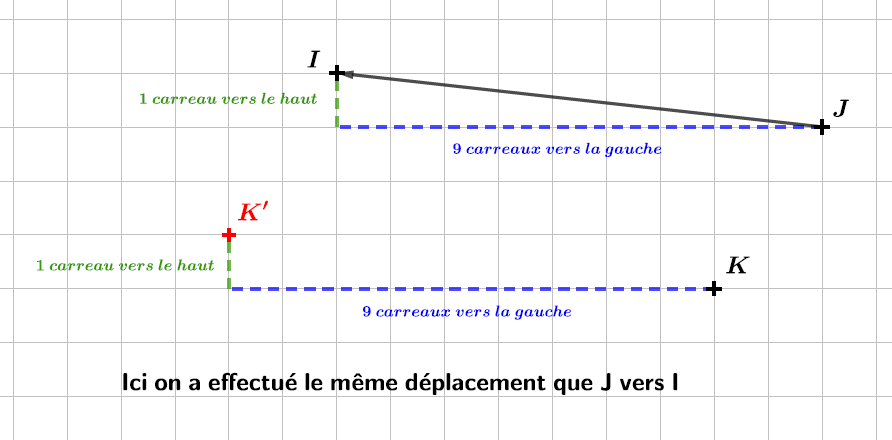
4°)4°) Ensuite en partant du point CC on effectue exactement le même déplacement.
Question 2

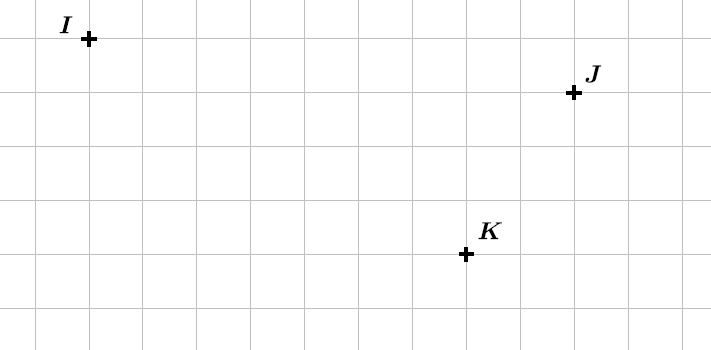
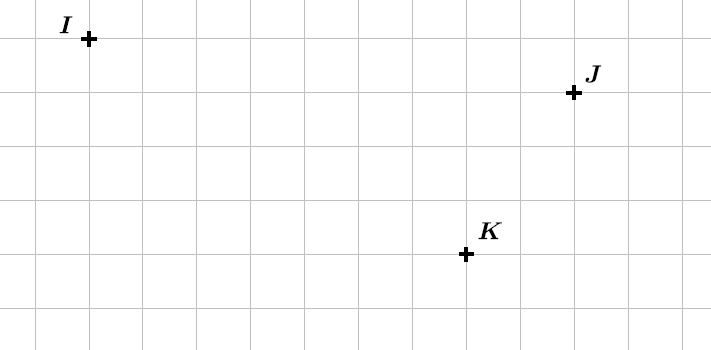
Construire à l'aide de la figure ci-dessous l'image du point KK par la translation qui transforme JJ en II.

Correction
    Définition d'une translation :

  • Une translation est une transformation géométrique qui permet d'obtenir par glissement d'une figure initiale une figure finale.
  • Ce déplacement, (glissement) doit s'effectuer sans que la figure initiale soit tournée ou déformée.
  • Ce glissement est défini par 3 éléments : un sens, une direction et une longueur.
Méthode pour tracer l'image d'un point par une translation à l'aide d'un quadrillage.
1°)1°) Il faut tracer le segment [IJ][IJ].
2°)2°) Partant du point JJ, on se déplace horizontalement pour arriver au niveau du point I.I.
(On part du point JJ car on demande la translation qui transforme JJ en II).
3°)3°) Puis on se déplace verticalement pour rejoindre le point II.
On peut également se déplacer verticalement puis horizontalement, cela ne change rien.
4°)4°) Ensuite en partant du point KK on effectue exactement le même déplacement.

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.