Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Construction d'un point par translation (Sans quadrillage) - Exercice 1

8 min
20
Question 1

Exemple : construire à l'aide de la figure ci-dessous l'image du point CC par la translation qui transforme 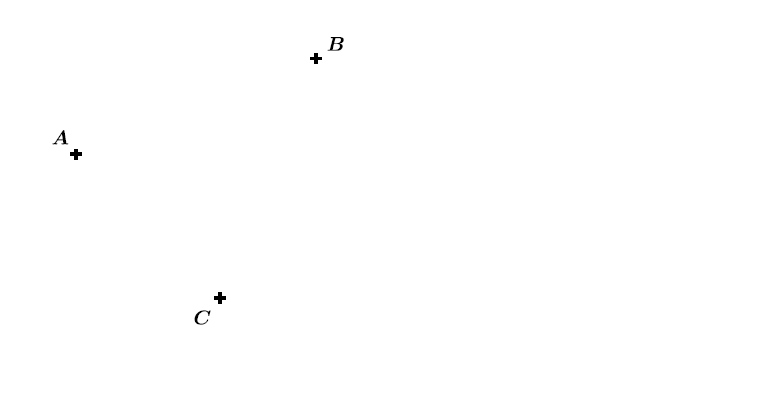AA en BB.

Correction
    Définition d'une translation :

  • Une translation est une transformation géométrique qui permet d'obtenir par glissement d'une figure initiale une figure finale.
  • Ce déplacement, (glissement) doit s'effectuer sans que la figure initiale soit tournée ou déformée.
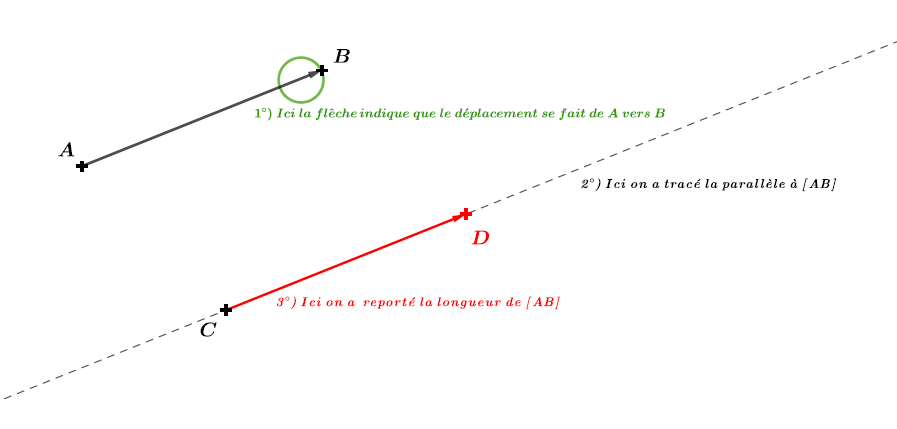
Méthode pour tracer l'image d'un point par une translation.
1°)1°) Il faut tracer le segment [AB][AB]. (Car on demande la translation qui transforme AA en BB.
2°)2°) On trace la droite parallèle au segment [AB][AB] qui passe par le point CC. (Cela nous donne le sens).
3°)3°) A l'aide d'un compas ou d'une règle, on mesure la longueur du segment [AB][AB]. (Cela nous donne la longueur).
4°)4°) A partir du point C,C, on reporte la longueur du segment [AB][AB] en prenant le même sens (même chemin) que AA vers BB.
5°)5°) A cette endroit ce trouve le point DD.
Question 2

Construire à l'aide de la figure ci-dessous l'image du point LL par la translation qui transforme KK en JJ.

Correction
    Définition d'une translation :

  • Une translation est une transformation géométrique qui permet d'obtenir par glissement d'une figure initiale une figure finale.
  • Ce déplacement, (glissement) doit s'effectuer sans que la figure initiale soit tournée ou déformée.
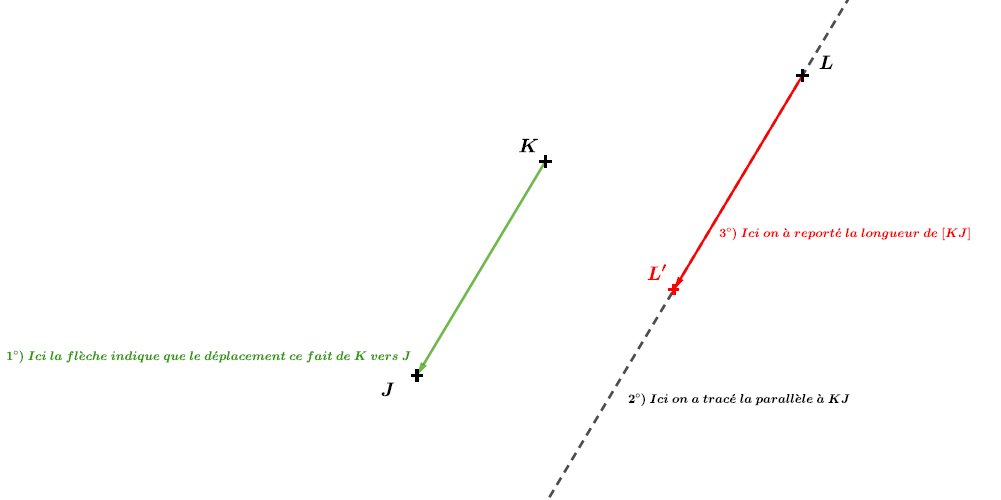
Méthode pour tracer l'image d'un point par une translation.
1°)1°) Il faut tracer le segment [KJ][KJ]. (Car on demande la translation qui transforme KK en JJ.
2°)2°) On trace la droite parallèle au segment [KJ][KJ] qui passe par le point LL. (Cela nous donne le sens).
3°)3°) A l'aide d'un compas ou d'une règle, on mesure la longueur du segment [KJ][KJ]. (Cela nous donne la longueur).
4°)4°) A partir du point L,L, on reporte la longueur du segment [KJ][KJ] en prenant le même sens (même chemin) que KK vers JJ.
5°)5°) A cette endroit ce trouve le point L′L'.